들어가기 전에
이 글은 2014년 KAIST Network Science 수업 중 Graph theory 내용을요약한 글이다. 이 렉쳐에서는 기본적인 Graph theory에 대해 배운다. 어려운 내용은 아니고 정말 기초적인 부분들에 대해서 다루게 된다.
Network and Graph
Network 혹은 Graph는 vertex와 그 vertex를 잇는 edge로 구성되어있는 일종의 collection이다. vertex와 edge는 node와 link라고 하기도 한다. 인터넷, 전력망, Citation network, social network 등을 예로 들 수 있으며, 요즘 내가 공부하고 있는 artificial neural network 역시 neuron과 synapse로 이루어진 graph이다. 보통 Graph는 mathematical하게 $G = (V,E)$로 표현이 된다. V는 vertex를 의미하며 E는 edge를 의미한다. 또한 일반적으로 n과 m이라는 notation도 사용하는데, n은 vertex의 개수, m은 edge의 개수이다. 이때 graph의 종류는 크게 두 가지가 있다. 하나는 directed graph이며 또 하나는 undirected graph이다. directed graph는 edge에 direction이 존재하여 한 vertex에서 다른 vertex를 point하는 형태가 되며, undirected graph는 edge에 특정한 direction이 존재하지 않는다. 또한 directed graph 중 Acyclic directed network 혹은 directed acyclic graph (보통 DAG라고 부른다) 라는 graph가 있는데, 이 그래프는 이름 그대로 cycle이 없는 graph를 얘기하며, 즉, 한 vertex에서 edge를 따라 이동했을 때 그 어떤 vertex, 그 어떤 path를 선택하더라도 자기 자신으로 돌아오지 않는 graph를 의미한다. 또한 graph의 edge는 weight라는 것을 가지고 있는데, 이 값은 edge의 고유한 값으로, 상황에 따라 다르게 해석이 된다. 예를 들어서 internet edge에서는 data flow의 양을 의미하기도 하고, social network에서는 얼마나 두 사람 간의 contact가 많냐 등으로 해석할 수도 있고, 단순한 geometric graph에서는 weight가 두 vertex간의 거리를 뜻하기도 한다. 렉쳐노트에는 weight가 non-negative라고 표현이 되어있지만, 실제 문제들에서는 edge가 negative weight를 가지는 경우도 많다. 물론 이런 경우 계산이 좀 복잡해진다.
Adjacency Matrix
그런데 이런 graph를 실제 분석하기 위해서는 어떻게 해야할까? 아래와 같은 그래프를 예로 들어보자.
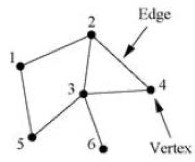
이 그래프는 간단한 undirected graph이며, 1,2가 연결되어 있고 2,3이 연결되어 있고…. 등등등이 연결되어있는 그래프이다. 그런데 우리가 어떤 그래프를 서술할 때에 있어서 항상 이렇게 일일이 어느 node와 어느 node가 연결되어있는지 명시해야할까? 이런 표현을 간단히 하기 위하여 Adjacent matrix라는 것이 도입된다. 이 matrix는 $A_{ij} = weight \ of \ edge \ from \ vertex \ j \ to \ i$ 로 표현이 된다. 당연히 두 vertex간에 edge가 없으면, 혹은 연결되어있지 않으면 그 값은 0이 된다. 즉, 위의 그래프는 아래와 같은 matrix로 간단하게 표현이 가능하다.

당연히 undirected graph는 이 adjacent matrix가 symmetric하며, self-edge가 없는 graph는 $A_{ii} = 0$ 이다.
또한 위에서 설명했었던 DAG를 adjacency matrix로 표현하면 재미있는 일이 벌어지는데, without loss of generality, 항상 DAG는 triangular matrix로 표현이 된다. Why? 왜냐하면, 아주 간단한 이유인데, DAG에서 어떤 path를 고르더라도 반드시 그 path는 cycle이 아니다. 즉, 다시 자기 자신으로 돌아오지 않기 때문에, 결국에는 outgoing edge가 없는 vertex에 도달하게 될 수 밖에 없다. (당연하다) 그러므로 반드시 최소한 하나 이상의 out degree가 0인 vertex에 도달하게 되고 (degree는 아래에서 더 자세히 설명) 이 말은 곧, column 중 하나는 반드시 zero-vector여야 한다는 소리이다. 이때 만약 out degree가 0인 vertex를 제거해보면 (이에 해당하는 edge도 제거하면) 그 zero vector를 pointing했던 vertex 역시 마찬가지 이유로 outdegree가 0인 vertex가 될 것이다. 이런 식으로 하나하나 제거해나가보면 결국, 반드시 triangular matrix로만 표현이 된다는 것을 알 수 있다. 또한 이런 triangular matrix의 eigenvalue는 diagonal element 들인데, DAG는 cycle이 없기 때문에 모든 diagonal element가 0이 되고 따라서 모든 eigenvalue는 0이 된다. 즉, 어떤 주어진 graph가 DAG인지 아닌지 여부를 판단하기 위해서는 간단하게 모든 eigenvalue들이 0이 되는지만 확인하면 되는 것이다.
Cocitation and Bibliographic Coupling
Cocitation이란 directed graph의 vertex i와 j를 동시에 point하고 있는 vertex들의 개수를 의미한다. 간단하게 ‘co-citation’이라는 단어 자체가 같이 citation한다는 의미이므로 그 의미 그대로 이해하면 된다. 그런데 이런 경우, 앞서 설명했던 adjacency matrix로 cocitation matrix를 표현하는 것이 가능하다. 그 이유는 vertex i,j를 동시에 point하는 k는 $A_{ik} A_{jk} = 1$ 이라는 식을 만족하기 때문이다. 따라서 모든 점들에 대해 이런 과정을 반복해보면 $C_{ij} = \sum_k^n A_{ik} A_{jk} = \sum_k^n A_{ik} A_{kj}^\top $라는 것을 알 수 있고, 이는 곧 $C = A A^\top$ 라는 것을 알 수 있다. 이 경우 임의의 matrix와 그 matrix의 transpose를 곱하면 그 결과는 항상 symmetric하다는 것이 잘 알려져 있다. 따라서 이 matrix는 symmetric하다. 이 결과는 당연하다고 할 수 있는데, i와 j에 대해 그 순서가 바뀐다고 해서 citation하고 있는 vertex가 달라지지는 않을 것이기 때문에 항상 $C_{ij} = C_{ji}$라는 것을 알 수 있다. 그리고 graph가 symmetric하다는 것은 이 graph가 undirected graph라는 것을 의미하게 된다. 그리고 이 graph는 weighted graph인데, 이 weight는 얼마나 많은 co-citation이 존재하는지를 indicate하는 숫자가 된다. 그리고 $C_{ii}$ 는 vertex i를 point하는 모든 edge의 개수를 의미한다.
Cociation이라는 것을 정의했으니 그 반대 방향을 생각할 수 있을 것이다. 즉, i와 j가 동시에 point하고 있는 vertex들의 개수를 생각해볼 수 있는데, 이 것을 Bibliographic Coupling이라 한다. 위와 같은 방법으로 유도를 해보면 $B = A^\top A$ 라는 사실을 알 수 있다. 마찬가지로 이 graph도 symmetric하며 따라서 이 graph도 undirected graph다. 또한 마찬가지로 이 graph는 weighted graph이며 그 weight는 얼마나 많은 vertex를 동시에 같이 point하고 있느냐를 의미한다. 마지막으로 $B_{ii}$ 는 vertex i가 point하는 모든 vertex의 개수를 의미한다.
이 두 가지 matrix는 directed graph에서의 search algorithm에 사용될 수 있다고 한다.
Bipartite Network
Hypergraph라는 것이 존재한다. Hyperedge라는게 존재하는 graph를 의미하는데, 이 hyperedge는 하나의 edge가 2개 보다 많은 vertex에 연결되어있는 edge를 의미한다. 이런 hypergraph를 표현하는 방법 중 하나는 bipartite graph를 사용하는 것이다. Bipartite graph는 vertex를 두 그룹으로 나누어 그룹 안에는 edge가 존재하지 않고, 모든 edge가 그룹 사이에서만 존재하는 graph를 의미한다. 즉, 아래 그림에서 까만점을 원래 hypergraph의 vertex, 하연점을 edge로 생각하면 우리가 일반적으로 알고 있는 graph로 hypergraph를 표현할 수 있는 것이다.
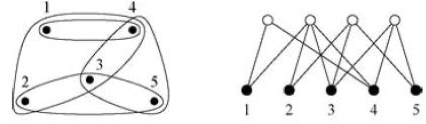
이런 bipartite matrix에는 incidence matrix라는 것이 존재하는데, 아래 그림과 같이 정의된다.

이 incidence matrix B는 projection을 위해 사용하는 것이 가능하다. 이때 projection은 edge들끼리 같은 vertex를 가지고 있는지 여부, 혹은 그 반대로 vertex끼리 같은 edge를 가지고 있는지 여부로 새로운 형태의 그래프를 그리는 것을 의미하며 아래에 그 간단한 예시가 나와있다.
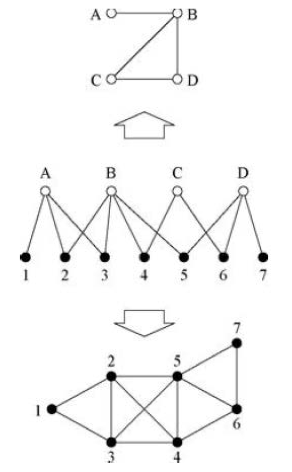
이때, i와 j가 같은 group k에 존재한다고 했을 때 우리는 $B_{ki} B_{kj} = 1$이라는 것을 알 수 있다. 따라서 i와 j가 몇 개의 같은 그룹에 속해있는지를 indicate하는 P는 $P_{ij} = \sum B_{ki} B_{kj} = \sum B_{ik}^\top B_{kj} $ 이며, 따라서 $P = B^\top B$ 라는 것을 알 수 있고, $P_{ii} = \sum B_{ki}^2 = \sum B_{ki}$ 라는 것을 알 수 있다. 따라서 $P_{ii}$는 vertex i가 속해있는 모든 group의 개수를 의미하게 된다.
Tree and Planer Network
Tree는 connected, undirected network의 일종으로, closed loop이 존재하지 않는 graph를 의미한다. 이 경우, 다시 말해서 parent가 단 하나만 존재하는 graph가 tree이며, 이 때문에 그 어떤 vertex pair를 고르더라도 그 사이를 연결하는 optimal path는 단 하나밖에 존재하지 않는다. 또한 n개의 vertex를 가지고 있는 tree의 edge개수는 반드시 n-1개이다.
Planar network는 서로 교차하는 edge가 하나도 없게 그릴 수 있는 graph를 의미한다. tree도 planar graph의 일종이다. 이런 planar graph는 반드시 4-coloring 보다 많은 색을 칠하는 것이 불가능하다는 것이 이론적으로 증명되어있다. Coloring problem은 graph를 any adjacent vertex pair가 서로 같은 색을 가지지 않도록 색을 칠해주는 문제인데, 4-coloring이라는 것은 4가지 색으로 색칠을 한다는 의미이다. 즉, planar graph에서 5-color problem은 반드시 풀 수 없는 문제이다.
그런데 일반적인 graph가 planar인지 아닌지 어떻게 판단할 수 있을까? Kuratowski’s theorem이라는 것이 있다. 모든 non-planar graph는 적어도 한 개 이상의 subgraph가 K5혹은 UG의 expansion이라는 theorem인데, 이를 통해 우리는 간단히 graph의 subdivision을 구해서 이 graph가 planar인지 아닌지 여부를 판단할 수 있다.
Degree
Degree는 vertex i와 연결된 모든 edge의 개수를 의미한다. notation은 $k_i$로 표현되며, $k_i = \sum_j^n A_{ij}$ 이며, $m = \frac {1} {2} \sum_i^n k_i = \frac {1} {2} \sum_{ij} A_{ij}$ 라는 것을 알 수 있다. degree의 평균은 c로 표현하는데, $1 \over n \sum_i^n k_i$ 이며, 이 값은 곧 $c = {2m \over n}$이다.
이에 대해 density 혹은 connectance라는 것을 정의할 수 있는데, 이것은 전체 존재 가능한 edge와 실제 존재하는 edge의 비율을 의미한다. 이 때 n개의 vertex가 있을 때 존재 가능한 edge의 개수는 단순히 n choose 2이므로 density $\rho$는 $\rho = \frac {m} {\binom {n}{2}} = \frac {2m} {n(n-1)} = \frac {c} {n-1}$으로 정의할 수 있다. 따라서 만약 dense한 graph는 n이 발산했을때 density가 constant일 것이고, sparse graph는 n이 발산하면 이 값이 0이 될 것이다. 이 방법을 사용해서 우리에게 주어진 graph가 densy한지 혹은 sparse한지 알 수 있는 것이다.
그리고 마지막으로 indegree와 outdegree라는 것이 있는데, 이것은 edge의 방향이 존재하는 directed graph에서만 정의되는 값으로, 당연히 indegree는 vertex i가 point하는 vertex의 개수고 outdegree는 vertex i를 point하는 vertex의 개수를 의미한다. 앞서 값을 살펴봤던 k(degree), m(edge number), c(density)를 살펴보면 아래와 같은 결과를 얻게 된다.
$$ k_i^{in} = \sum_j^n A_{ij}, \ k_j^{out} = \sum_i^{out} A_{ij} $$
$$ m = \sum_i^n k_i^{in} = \sum_j^n k_j^{out} = \sum_{ij} A_{ij} $$
$$ c_{in} = \frac {1} n \sum_i^n k_i^{in} = \frac 1 n \sum_j^n k_j^{out} = c_{out} $$
$$ c = \frac {m} {n} $$
Path and component
Path는 모든 consecutive pair가 서로 connected edge의 sequence로 나태어지는 vertex들의 sequence를 의미한다. 즉, 주어진 vertex set을 순서대로 살펴보게되면 각 consecutive vertex pair 사이에는 edge가 존재하는 vertex set을 path라고 하는 것이다. 그냥 우리가 알고 있는 그 path를 수학적으로 정의한 것에 불과하니 넘어가도 그만이다. Path의 길이는 이 lecture는 path기 traversed한 edge의 개수로 정의하는데, 개수가 아니라 그 edge들의 weight들의 summation으로 일반적으로 정의한다.
아무튼 이 lecture에서 정의한대로 path의 length를 정의했을 때 주어진 graph에서 length가 r인 path의 개수는 어떻게 찾을 수 있을까? Adjacent matrix에서 $A_{ik} A_{kj}$를 계산하게 되면 k를 경유하는 i에서 j로 가는 모든 path의 개수가 나오게 된다. 이 사실로 부터 다음과 같은 결론을 유추해낼 수 있다. 아래에서 U는 orthogonal matrix of eigenvector를 의미하고 $k_i$는 i번째로 큰 eigenvalue를 의미한다. (간단한 eigenvector decomposition이다)
$$ N_{ij}^r = |A^r|_{ij} $$
$$ L_r = \sum_i^n |A^r|_{ij} = Tr A^r = Tr(UK^r U^\top )$$
$$ = Tr(U^\top U K^r) = Tr K^r = \sum_i k_i^r $$
Geodesic path라는 것이 있는데, shortest path의 일종이다. 이때 shortest path를 weight의 sum이 아니라 단순히 hop의 개수만 세는 방식으로 계산하는 것이다. 일반적으로 graph의 diameter를 측정한다고 했을 때는 이 값을 사용한다.
Eulerian path라는 것도 있는데, 모든 edge를 정확히 한번만 visit할 수 있는 path를 의미하며, Hamiltonian path는 모든 vertex를 한 번씩 visit하는 path를 의미한다. Euler path는 이전에 인터넷 속의 수학에서 설명했었던 쾨르히스베르크 다리 문제를 풀 때 사용할 수 있다. 이 path는 job sequencing, garbage collection, parallel programming등에 사용할 수 있지만 이 path를 찾는 방법은 NP-complete이기 때문에 빠른 시간 안에 찾을 수는 없고 보통 approximation algorithm을 사용하게 된다.
component는 graph의 subgraph를 의미한다. 이 때 component 안의 vertex를 모두 visit하는 path가 최소한 하나 이상 존재해야한다. out-component는 특정 vertex A에서 시작해 도달 가능한 vertex들의 set이며, in-component는 vertex A로 도달 가능한 path를 가지는 vertex들의 set이다.
Independent 혹은 disjoint path라는 것도 정의할 수 있는데, edge independent는 두 개의 path가 서로 공유하는 edge가 없는 경우이며, 당연히 vertex independent는 공유하는 vertex가 없는 경우를 의미한다. vertex indep이면 edge indep하지만 그 반대는 항상 성립하는 것은 아니다. 이 때 given vertex pair 사이에 존재하는 모든 independent path의 개수를 connectivity로 정의할 수 있다. 이 값은 두 vertex가 얼마나 많은 connectivity를 가지고 있는지, 혹은 그 둘 사이의 bottleneck이 얼마나 될지를 판단할 수 있는 지표가 된다.
Cut sets
cut set은 그에 속하는 vertex 혹은 edge등을 제거했을 때 특정한 vertex들의 pair가 disconnected되는 set을 의미한다. 또한 minimum cut set은 그런 cut set 중에서 가장 작은 element를 가지는 cut set을 의미한다.
Menger’s Theorem에 따르면, given pair of vertices의 minimum vertex cut set의 크기는 같은 pair의 connectivity와 같다고 한다.
또한 두 vertex사이의 max flow라는 것을 edge-independent path의 개수 곱하기 capacity로 정의할 수 있는데, 이런 max flow를 정의했을 때, max-flow/min-cut theorem에 따르면 vertex pair의 maximum flow는 항상 minimum cut set와 single path의 capacity의 곱과 같다고 한다. 이때 undirected graph에 대해서 edge connectivity와 minimum edge cut set의 size와 maximum flow의 크기가 같다는 것이 증명될 수 있다.
Graph Laplacian
어떤 commodity 혹은 substance의 flow가 어떤 비율로 흘러가느냐에 따라 Diffusion이라는 것을 정의할 수 있다. 약간 복잡한 얘기인데, 약간 불필요해보이기도 하고 복잡해서 링크로 대체하겠다. 링크에서도 나오듯 결국에는 Random walk를 정의하기 위해서 나온 개념으로 보이므로 생략하도록 하겠다.
KAIST Network Science
다른 요약글들 보기 (카테고리로 이동)
- Lecture 1: Introduction
- Lecture 2: Graph Theory
- Lecture 3: Measures and Metric
- Lecture 4: Random Network
- Lecture 5: Small world Network
- Lecture 6: Scale free Network