README   SanghyukChun's Blog

고흐의 그림을 따라그리는 Neural Network, a Neural Algorithm of Artistic Style (2015)

| Comments

얼마 전, ‘A Neural Algorithm of Artistic Style ’ 이라는 이름의 충격적인 논문이 arXiv에 업로드되었다. 기술 전문 잡지나 신문이 아닌 스브스뉴스 같은 일반적인 기사를 보도하는 매체에서도 보도가 되었을 정도로 요즘 꽤 이슈가 되고 있는 논문이다.

자고로 백문이 불여일견이라, 이게 도대체 무슨 contribution이 있길래 사람들의 이목이 쏠리고 있는지 논문에 첨부되어있는 그림을 먼저 보자.

이 그림들은 모두 사람이 그린 것이 아니라 neural network를 사용하여 generate한 것이다. 이 논문은 제목 그대로, ‘artistic style’을 learning하는 neural network algorithm을 제안한다. 여기에서 artistic style이라는 것을 어떻게 정의하였는지는 나중에 조금 더 자세히 살펴보도록하자. 위 그림은 이 논문에서 제안한 알고리즘을 사용하여 report한 결과이다. 원본이 되는 A가 독일의 튀빙겐이라는 곳에서 찍은 ‘사진’이다. B부터 F는 유명한 거장들의 그림 ‘style’과 A의 ‘content’를 가지는 그림을 generate한 결과이다. 순서대로 B는 J.M.W. 터너의 <미노타우르스 호의 난파>, C는 그 유명한 빈센트 반 고흐의 <별이 빛나는 밤>을, D는 뭉크의 <절규>, E는 피카소의 <앉아 있는 나체의 여성>, F는 칸딘스키의 <구성 VII>이다. 놀랍게도 알고리즘을 통해 얻은 그림은 원본 사진의 content는 거의 그대로 보존하면서, 동시에 다른 그림의 style을 특징을 잘 살려서 가지고 있다.

이 짧은 논문이 사람들에게 얼마나 큰 충격을 주었는지는 길게 적지 않아도 알 수 있을 것이라고 생각한다. 논문이 나오고 얼마 지나지 않아 jcjohson 이라는 github user가 torch 기반으로 만든 ‘neural style’이라는 프로젝트를 github에 공개하였다. 논문이 정말 좋은 결과를 낸 것인지 사람들이 이런 저런 사진과 그림들을 사용해 실험해본 결과, 논문에서 이야기하는 것 처럼 실제로 아무 사진을 적당히 골라서 적당한 그림을 넣어주면 사진의 내용은 보존한 채로 질감만 바꿔서 출력해주는 것을 알 수 있었다. 아래 그림은 ‘neural style’을 사용해 금문교 사진과 여러 예술가들의 그림을 사용해 generate한 결과이다.

이 논문이 나온게 9월 말이었는데, 벌써 한국 개발팀에서 스마트폰 app까지 개발했을 정도로 관심이 뜨겁다. (스브스뉴스: 이건 ‘반 고흐’의 그림이 아닌 ‘컴퓨터’의 그림입니다.)

꽤나 흥미로운 논문인 만큼, 어떤 아이디어를 사용했고, 어떤 방법론을 사용했는지까지 한 번 차근차근 살펴보도록 하자.

Content & Style Reconstruction using CNN

Deep learning이 지금처럼 급부상하게 된 배경에는 (비전 분야를 중심으로 한) CNN의 엄청난 힘이 있었다. CNN이 비전에서 월등한 성능을 내는 이유를 여러가지로 설명할 수 있겠지만, 일반적으로는 CNN은 각각의 layer가 ‘feature’의 의미를 지니기 때문이라고 설명한다. 각각의 layer가 feature를 생성해내고, 이 feature들이 hierarchy하게 쌓이면서 더 높은 layer로 갈수록 더 좋은 feature를 만들어낸다는 것이다. CNN은 이 feature를 hard-coding하여 뽑아내는대신, 데이터에서부터 ‘가장 좋은’ 최종 feature를 만들도록 학습시키기 때문에 아주 좋은 feature를 사용해 perceptron 등의 간단한 classifier로 높은 performance를 얻게 되는 것이다 (CNN에 익숙하지 않다면 CNN에 대해 설명했었던 이전 글을 참고하면 좋을 것 같다). 그렇기 때문에 각각의 convolution layer의 output은 흔히 feature map으로 표현이 된다.

주어진 이미지에서 feature를 뽑아내는 것은 CNN을 통하여 지금까지 항상 하던 일이었다. 그렇다면 반대로 할 수도 있지 않을까? 즉, CNN의 중간 feature map을 사용하여 원래 이미지를 복원하는 작업을 하는 것이다. 이렇게 feature map에서부터 이미지를 reconstruction 할 수만 있다면, deep CNN에서 layer를 지면서 어떤 재미있는 일들이 벌어지고 있는지 사람이 직접 눈으로 확인할 수 있을 것이다. 이런 visualization에 대한 motivation 때문에 그 동안 CNN의 convolution layer에서 원래 이미지를 reconstruction하는 작업들은 꾸준하게 제안되어 왔다. 그 중 가장 유명한 work으로 다음과 같은 work이 있다.

이 논문은 주어진 feature map에서 image를 복원하는 방법을 제안한다. 단순히 이미지를 복원하는 것이 아니라, 이미지를 특정 목적에 맞게 변형하는 work도 진행되어왔다. 대표적인 예가 아래 논문과 Google DeepMind의 Deep Dream이다.

이 논문은 deep CNN이 거의 100% 확률로 오답을 발생시키도록 이미지를 조작한 work이다. 예를 들어 주어진 이미지가 ‘새’ 라는 label을 가지고 있다고 판별했을 때, ‘문어’라는 label을 100% 로 가지도록 이미지를 조작하는 것이다. 사람이 봤을 때는 여전히 ‘새’ 사진이지만, CNN은 ‘문어’라고 판별해버리는 것이다.

이렇듯, 다양한 목적으로 CNN이 이미 주어져 있을 때, 특정 목적에 따라 이미지를 update하는 방법론들은 이미 예전부터 연구가 계속 진행되어왔다. 위에 링크한 3개의 work은 꽤 흥미로운 주제들이기 때문에 나중에 또 따로 포스팅할 수 있도록 하겠다. 이 논문의 contribution은 각 convolution layer에서부터 style과 content를 reconstruct하는 방법론을 제안했다는 것이다. 이 방법은 앞에서 언급한 Understanding deep image representations by inverting them 논문 처럼 현재 feature map에서 원래 이미지를 최대한 복원하는 content reconstruction과, 아래 논문 등에서 제안되어왔던 texture 분석과 생성 등을 복원하는 texture reconstruction을 결합한 것이다. 참고로 이 work들은 맨 처음 논문을 제외하면 neural network 기반 work은 아니다 (첫 번째 논문은 이 논문을 작성한 연구팀이 이 논문을 arXiv에 올리기 3개월 전에 arXiv에 올린 다른 논문이다). 자세한건 뒤에서 더 다루도록하자.

이 논문에서 제안하는 두 가지 reconstruction 방법을 CNN의 각 layer에 대해 적용해보면 다음과 같은 결과를 얻을 수 있다. 참고로 이 논문에서는 CNN 모델로 VGG 19를 선택했다. 이 네트워크는 총 16개의 convolution layer와 3개의 fully connected layer로 이루어져있다. 이 네트워크에 대한 설명은 method 부분에서 더 자세히 다루도록 하겠다.

위 그림은 CNN 하나에서 서로 다른 두 가지 방법으로 각각 style과 content를 layer 별로 reconstruction한 결과이다. 하나의 같은 CNN에 대해 두 가지 다른 reconstruction을 진행한 것인데, 위쪽 그림은 고흐의 <별이 빛나는 밤>의 style을 layer 별로 reconstruction한 것이고, 아래 그림은 튀빙겐에서 찍은 사진의 content를 layer 별로 reconstruction한 것이다.

먼저 style reconstruction에서 알 수 있는 것은 layer가 얕을수록 원래 content 정보는 거의 무시하고 ‘texture’를 복원한다는 것이다. 반면 깊은 layer로 가게 될수록 점점 원래 content 정보가 포함이 되는 것을 볼 수 있다. 이런 현상이 발생하는 이유는 이 논문에서는 style을 같은 layer에 있는 feature map들 간의 correlation으로 정의하기 때문이다. 이를 구체적으로 어떻게 수학적으로 정의하였는지는 뒤에서 좀 더 자세하게 살펴보도록 하자. Style을 correlation으로 생각하기 때문에, 가장 style이 복원이 잘되는 얕은 layer에서는 원본 content가 거의 무시되고 correlation을 가장 좋게하는 style만 나오는 것이고, 깊은 layer로 갈수록 style이 제대로 복원이 되지 않을 것이므로 원본 content의 정보가 증가해 correlation이 작아지는 결과를 얻게 되는 것이다.

다음으로 content reconstruction을 보자. 이 그림을 통해 낮은 level의 layer는 거의 완벽하게 원본 이미지를 보존하고 있고 layer가 깊어질수록 원본 이미지의 정보는 조금씩 소실되지만, 가장 중요한 high-level content는 거의 유지가 되는 것을 볼 수 있다.

이 논문은 같은 CNN이라고 할지라도 content와 style에 대한 representation이 분리가 되어있다는 것을 중요하게 언급하고 있다. 그렇기 때문에 같은 network을 사용하여 서로 다른 이미지에서 서로 다른 content와 style을 reconstruction해서 그 둘을 섞는 것이 가능한 것이다. 이것이 중요한 이유는 실제로 reconstruction을 하는 과정은 임의의 image를 input으로 삼고, image를 parameter로 하여 목표하는 style과 content에 대한 loss를 minimize하는 optimization 과정이기 때문이다. 이 두 가지 다른 optimization process를 오직 하나의 network만 사용하여 진행할 수 있기 때문에 $A$(혹은 튀빙겐에서 찍은 사진)이라는 input의 content를 가지면서 $B$(혹은 고흐의 <별이 빛나는 밤>)이라는 input의 style을 가지도록하는 방향으로 input 이미지의 gradient를 구할 수 있는 것이다. 수식으로 나타내보자. input image를 $x$라고 해보자. 우리 목표는 $x$와 $A$ 간의 content가 얼마나 다른지 표현하는 loss function $\mathcal L_{content} (x,A)$와 $x$와 $B$ 간의 style이 얼마나 다른지 표현하는 loss function $\mathcal L_{style (x,A)}$를 minimize하는 $x$를 찾는 것이다. 따라서 우리가 풀고 싶은 optimization problem은 다음과 같다.

$$x = \arg\max_x \alpha\mathcal L_{content} (x,A) + \beta\mathcal L_{style} (x,B)$$

이런 식으로 식을 쓸 수 있을 것이다 ($\alpha$와 $\beta$는 적당한 상수라고 하자). 이런 optimization을 푸는 가장 간단한 방법으로 $x$에 대한 gradient를 구하고 gradient descent optimization을 하는 것인데, 두 loss를 같은 network에 대해 design할 수 있기 때문에 gradient가 간단해지는 것이다. 그러면 이제 구체적으로 어떻게 각각의 loss가 정의되었는지 살펴보자.

Methods

이 paper에서는 CNN 모델로 VGG 19 네트워크를 사용한다. 이 네트워크는 옥스포드의 VGG(Visual Geometry Group)에서 만든 네트워크로, Batch Normalization이 적용되기 이전 inception network (혹은 GoogleNet) 등에 비해 꽤 우수한 성능을 보이는 네트워크이다. 아래 논문을 통해 발표하였다.

자세한 method를 설명하기에 앞서 VGG 19 네트워크 자체에 대해 다뤄야하는데, 이 네트워크는 총 16개의 convolution layer, 5개의 pooling layer, 3개의 fully connected layer로 구성되어있다. 이 논문은 제공된 16개의 convolution layer에서 생성되는 feature map을 사용해 style loss와 content loss를 계산한다. 이 네트워크는 다음과 같은 형태로 구성되어있다.

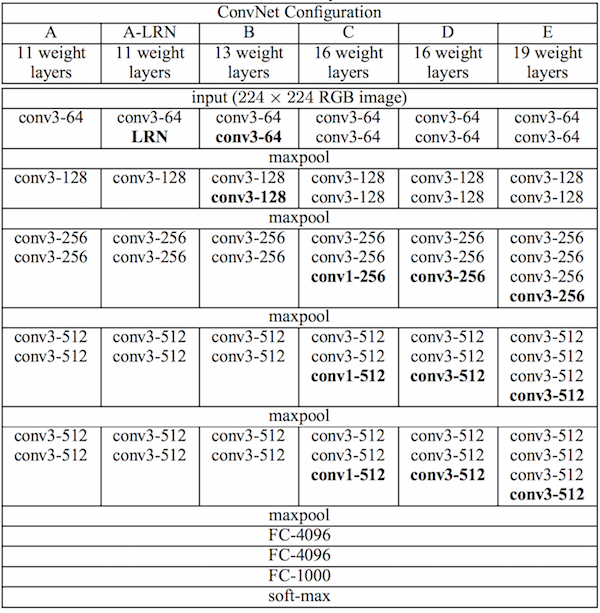
이 논문에서 사용한 VGG 19는 E에 해당하며, conv 2개 - pooling - conv 2개 - pooling - conv 4개 … 이런 식으로 구성되어있다. 각각의 conv layer들은 pooling layer를 기준으로, 순서대로 conv 1_1, conv 1_2, conv 2_1, conv 2_2, conv 3_1, conv 3_2, conv 3_3, … conv 5_4 라는 이름을 가지고 있다. 즉, conv 5_1 이면 4번쨰 pooling layer 바로 다음 conv layer를 말하는 것이다.

이 논문에서는 fully connected layer는 사용하지 않고, 16개의 conv layer와 5개의 pooling layer만 사용하는데, image reconstruction에 있어서는 max pooling보다는 average pooling을 고르는 것이 그림이 조금 더 자연스럽고 좋아보이는 결과로 나오기 때문에 max pooling 대신 average pooling을 사용하였다고 한다.

그럼 먼저 비교적 간단한 content loss 부터 살펴보도록하자. 이 논문은 feature map을 $F^l \in \mathcal R^{N_l \times M_l}$으로 정의하였다. 이때 $N_l$은 $l$ 번째 레이어의 filter 개수이고, $M_l$은 각각의 filter의 가로와 세로를 곱한 값이며, 즉 각 filter들의 output 개수이다. 또한 $F^l_{ij}$는 $i$ 번째 필터의 $j$ 번째 output을 의미하게 된다. 이제 우리가 비교하려는 두 가지 이미지를 각각 $p$와 $x$라 하고, 각각의 $l$ 번째 layer의 feature representation을 $P^l, F^l$로 정의하자. 이렇게 정의하였을 때, $l$ 번째 layer의 content loss는 다음과 같이 간단하게 정의된다.

$$ \mathcal L_{content} (p, x, l) = \frac{1}{2} \sum_{ij} \big( F^l_{ij} - P^l_{ij} \big)^2. $$

즉, $p$와 $x$에 대해 각각 feature map $P^l, F^l$을 계산하고, 이 둘의 차의 Frobenius norm ($\| P^l - F^l \|_F$)을 loss로 선택한 것이다. 이 error를 각각의 layer에 대해 따로 정의하게 된다. 이제 튀빙겐에서 찍은 사진 $p$의 $l$ 번째 layer의 representation을 사용해 image reconstruction을 한다고 가정해보자. 이때 $l$ 번째 layer에서 복원한 이미지를 $x^l$라고 하자. 앞서 정의한 loss를 minimize하는 $x^l$를 찾아야하므로, 우리는 다음과 같은 식을 얻는다.

$$x^l = \arg\max_x \mathcal L_{content} (p, x, l). $$

이 식을 풀기 위한 가장 간단한 방법은 $x^l$을 random image로 initialize하고 $\frac{\mathcal L_{content} (p, x, l)}{x}$를 게산해 gradient descent method를 사용하는 것이다. Loss를 layer의 각각의 activation으로 미분한 결과는 다음과 같다.

$$ \frac{\partial \mathcal L_{content} (p, x, l)}{\partial F^l_{ij}} = (F^l_{ij} - P^l_{ij})_{ij} \mbox{ if } F^l_{ij} > 0, \mbox{ otherwise, } 0.$$

이 값을 사용하면 전체 gradient를 back-propagation 알고리즘을 사용해 간단하게 계산할 수 있게 된다. 앞서 봤던 reconstruction 그림의 아래 부분에서 복원한 5개의 이미지는 각각 conv 1_1, conv 2_2, conv 3_1, conv 4_1, conv 5_1에서 loss를 계산하여 복원한 것이다.

다음으로, style에 대한 loss를 정의해보자. 이 논문에서 style이라는 것은 같은 layer의 서로 다른 filter들끼리의 correlation으로 정의한다. 즉, filter가 $N_l$개 있으므로 이것들의 correlation은 $G^l \in \mathcal R^{N_l \times N_l}$이 될 것이다. 이때, correlation을 계산하기 위하여 각각의 filter의 expectation 값을 사용하여 correlation matrix를 계산한다고 한다. 즉, $l$번째 layer에서 필터가 100개 있고, 각 필터별로 output이 400개 있다면, 각각의 100개의 필터마다 400개의 output들을 평균내어 값을 100개 뽑아내고, 그 100개의 값들의 correlation을 계산했다는 것이다. 이렇게 계산한 matrix를 Gram matrix라고 하며 $G^l_{ij}$라고 적으며 다음과 같이 계산할 수 있다.

$$ G^l_{ij} = \sum_{k} F^l_{ik} F^l_{kj}.$$

두 개의 image $a$와 $x$ 간의 style이 얼마나 다른지를 나타내는 style loss $\mathcal L_{style}$은 $G^l_{ij}$를 사용하여 다음과 같이 정의된다.

$$ \mathcal L_{style} (a,x) = \sum_{l=0}^L w_l E_l $$

$L$은 loss에 영향을 주는 layer 개수, $w_l$은 전부 더해서 1이 되는 weight이고, $E_l$은 layer $l$의 style loss contribution이다. 이 값은 다음과 같이 정의된다.

$$ E_l = \frac{1}{4 N_l^2 M_l^2} \sum_{i,j} \big( G^l_{ij} - A^l_{ij} \big)^2. $$

역시 마찬가지로, $p$, 혹은 고흐의 <별이 빛나는 밤>의 layer 별 style reconstruction 역시 이 $\mathcal L_{style} (a,x)$를 minimize하는 $x$를 찾는 것으로 풀 수 있으며 이 문제는 back-propagation algorithm으로 풀 수 있다.

$$ \frac{\partial \mathcal E_l}{\partial F^l_{ij}} = \frac{1}{N_l^2 M_l^2} \sum_{i,j} \big( \big(F^l)^\top \big( G^l_{ij} - A^l_{ij} \big)\big)_{ji} \mbox{ if } F^l_{ij} > 0 \mbox{ otherwise } 0. $$

다시 한 번 앞서 봤던 reconstruction 그림의 윗 부분에서 복원한 이미지를 살펴보면, 순서대로 loss 계산을 위해 conv 1_1만 사용하여 복원한 그림, conv 1_1, conv 2_1을 사용한 그림, conv 1_1, conv 2_1, conv 3_1을 사용한 그림, conv 1_1, conv 2_1, conv 3_1, conv 4_1을 선택한 그림 … 이런 식으로 선택하여 복원을 한 그림이다. 이때 ‘선택’ 한다는 것의 개념은 선택한 layer의 $w_l$의 값을 0이 아닌 같은 값으로 두고 나머지는 전부 0으로 설정하는 것이다. 예를 들어 c 그림은 4개만 영향을 주므로 conv 1_1, conv 2_1, conv 3_1, conv 4_1만 $w_l = 0.25$이고 나머지는 0이다.

이제 마지막으로 이 두 가지 loss를 한 번에 optimization하는 과정만 남았다. $\alpha$와 $\beta$는 content와 style 중 어느 쪽에 더 초점을 둘 것인지 조정하는 파라미터로, 보통 $\alpha/\beta$으로 $10^{-3}$이나 $10^{-4}$ 정도를 고른다고 한다.

$$\mathcal L_{total} (p,a,x) = \alpha \mathcal L_{content} (p, x) + \beta \mathcal L_{style} (a,x)$$

논문에서는 style에 얼마나 많은 layer를 고려하는지에 따라, 그리고 $\alpha/\beta$의 값을 조정함에 따라 다음과 같이 결과가 달라진다고 report하고 있다.

x 축이 $\alpha/\beta$, y축은 순서대로 앞에서처럼 conv 1_1, conv 2_1, conv 3_1, conv 4_1, conv 5_1을 선택한 것이다 (A: 1_1, B: 1_1, 2_1, C: 1_1, 2_1, 3_1, …) 이 값들을 어떻게 조정하느냐에 따라 style과 content의 적당한 trade-off를 조정할 수 있다. Layer를 더 많이 사용할수록, 그리고 $\alpha/\beta$ 값이 작아질수록 content보다는 style에 더 치중된 결과가 나오게 된다. 그리고 당연히 layer를 더 적게 사용하거나 $\alpha/\beta$의 값을 키울수록 그 반대의 결과가 나오게 된다.

위 그림은 앞에서 언급한 ‘neural style’을 사용해 만든 그림이다. 원본 content 이미지로 브래드 피트의 사진을 넣고, style 이미지로 피카소의 <자화상>을 넣은 다음, $\alpha/\beta$ 값을 조정하면서 값이 변하는 것을 관측한 것이다.

맨 처음 글을 시작하며 보았던 그림에서는, content representation은 conv 4_2의 것만을 사용하고, style representation은 conv 1_1, 2_1, 3_1, 4_1, 5_1 에 각각 $w_l = 1/5$, 나머지는 $w_l=0$으로 하여 사용했다. 또한 B,C,D 그림은 $\alpha/\beta = 10^{-3}$, E,D 그림은 $\alpha/\beta = 10^{-4}$를 사용하였다고 한다.

Comments

  • 개인적인 생각으로는, 이 논문의 결과는 고흐나 뭉크 등의 ‘스타일’이 분명한 인상주의, 표현주의, 야수파 화풍의 화가들의 그림을 더 잘 generate할 것으로 생각된다. 나중에 사람들이 실험해본 결과도 그렇고, 대체로 고흐 등의 경우 스타일이 특색이 뚜렷해서 그러한지 꽤 그럴싸한 결과가 나오는 반면, 피카소 등으로 대변되는 입체파 처럼 ‘스타일’을 넘어서는 그 무언가가 존재하는 경우 기대만큼 좋은 결과로 이어지는 것 같지는 않다. 원래 이 논문에서 제안하는 알고리즘의 목적 자체가 그림의 texture를 learning하여 content는 유지한 상태로 texture만 변경시키는 것이므로, 내용 자체가 변화하는 입체파 등의 독특한 그림을 제대로 따라하는 것은 불가능하기 떄문에 그런 것으로 보인다. (+ 글을 쓰면서 개인적으로 궁금해진게, 캐리커쳐는 어떻게 반응할지 궁금해졌다. 나중에 public하게 공개된 코드를 사용해서 실험해봐야겠다)
  • 왜 method에서 전체 conv layer를 사용하는 것이 아니라 일부만 사용하는 것인지 다소 아리송하다. 또한 왜 style reconstruction을 위해 conv 11, 21, … 51 의 정보만 사용했고, content는 왜 conv 42를 사용하였는지 역시 의아하다. 아마 제일 잘 되는 것을 골랐을텐데, 왜 그것들이 제일 잘되는 것일까 궁금해진다.
  • CNN에 대한 이해가 충분히 있어야 쉽게 읽을 수 있는 논문이었다. 추가로 VGG network에 대한 이해도도 있으면 도움이 되는 것 같다. 맨 처음 논문을 읽을 때는 이런 것들에 대해 감이 좀 약해서 읽어도 이해하기가 어려웠는데, CNN 공부를 다시 끝내고 다른 선행 연구들을 적당히 이해한 채로 다시 읽어보니 쉽게 이해할 수 있었다.

Summary of A Neural Algorithm of Artistic Style

  • CNN의 conv layer가 feature map이라는 것에서부터 착안하여, feature map에서 style과 content를 reconstruct하는 optimization problem을 제안하였다.
  • 하나의 CNN에서 content와 style representation이 separable하므로 style과 content를 한 번에 update하는 알고리즘을 만들 수 있다.
  • Content loss는 두 이미지 각각의 feature matrix의 차의 frobenius norm으로 표현이 된다. 최종 결과를 위해서는 conv 4_2 만 사용하였다.
  • Style loss는 두 이미지 각각의 Gram matrix의 차의 frobenius norm으로 표현이 된다. 최종 결과를 위해서는 conv 11, 21, 31, 41, 5_1 만 사용하였다.
  • 이때 style loss가 Gram matrix가 되는 이유는 style을 한 레이어 안에 있는 filter들의 correlation으로 정의했기 때문이다. 이때 correlation 계산은 각각의 filter들의 expectation 값들을 사용한다.
  • VGG 19 네트워크를 사용했으며, FC layer는 제거하고 max pooling 대신 avg pooling을 사용하였다.
  • Content loss와 Style loss의 비율을 조정하여 style과 content 중에서 어느 것에 집중할지 선택할 수 있다. 논문에서는 0.001 정도를 사용하였다.

Reference