AlphaGo의 알고리즘과 모델

들어가며
왜 바둑이 체스보다 어려운가?
Monte-Carlo Tree search
Approaches by AlphaGo
정리
References
변경 이력

들어가며

근 일주일 동안 가장 뜨거웠던 주제를 하나 꼽으라면 누가 뭐래도 “알파고”일 것이다. 글을 쓰고 있는 2016년 3월 13일 기준으로 알파고와 이세돌 사범과의 경기에서 최종 승리를 확정지은 상태이며, 오늘 이세돌 사범이 첫 승을 거둠으로써 5국 중 3대 1의 상황이 되었다. 내일 모레 있을 경기에서 3-2가 될지 4-1이 될지가 최종 결정이 될 것이며, 어느 결과가 나오더라도 AI 분야에서는 기념비적인 사건이 될 것이다.

덕분에 AI (정확하게는 딥러닝)이 사람들의 이목을 집중적으로 받게되면서 불분명한 정보가 마구 흘러다니는 것 같아서 제대로 딥마인드에서 어떤 모델과 알고리즘을 사용한 것인지 직접 알아보고 정리해보기로 했다. 이 글에서는 deep learning, CNN [7], deep Q-learning [9]등의 용어들을 설명없이 사용할 예정이므로, 해당 개념들에 관심이 있다면 내가 쓴 이전 글들 [7], [9] 이나 다른 외부 자료들을 참고하면 좋을 것 같다. 이 글은 Google Deep Mind에서 2016년 Nature에 발표한 matering the Game of Go with Deep Neural Network and Tree Search [1]를 기반으로 작성되었다.</p>

왜 바둑이 체스보다 어려운가?

글을 본격적으로 시작하기 전에, 왜 바둑이 체스나 다른 게임들보다 어려운지부터 이야기해보자. 체스 (1997년 IBM Deeper blue), 체커 (1994년 CHINOOK [6]), tic tac toe (1952년) 등의 게임들은 이미 오래오래 전에 컴퓨터가 인간을 박살낸 분야이다. 게다가 최근 연구들을 통해 Atari 에뮬레이터를 기반으로 한 비디오 게임에서도 굉장히 뛰어난 성능을 내는 모델이 제안된 바 있다 [9]. 그런데 바둑은 왜 아직까지 인간을 뛰어넘기가 어려웠을까? 그 이유는 다른 데에 있는 것이 아니라, 바둑에서 발생할 수 있는 경우의 수가 너무나 많기 때문이다. 체스, 바둑 등의 턴 방식의 게임들은 현 상황에서 앞으로 발생할 수 있는 모든 경우의 수에 대한 search tree를 만들고 가장 최적의 path를 찾아가는 방식으로 게임을 플레이하게 되는데, 이 tree의 size는 각 위치 별로 가능한 가능한 모든 movement의 개수 b와 게임의 길이 d의 조합인, $b^d$로 표현된다. 참고로 b는 breadth이고, d는 depth이다. 체스의 경우 b는 약 35, d는 약 80이지만, 바둑은 b가 약 250 d는 약 150이나 된다 (착수 가능한 경우의 수가 평균 250개, 평균 게임 길이가 150수). 10진수로 바꾸면 $250^{150} \simeq 10^{360}$이 되는데, 이게 얼마나 대단한 숫자이냐 하면 우주의 모든 원자의 숫자가 약 $10^{80}$으로 예상되니까, 각 경우 수마다 원소 하나 씩을 대응시키면 $10^{280}$개의 우주가 필요한 셈이다.

…사이즈가 너무 커서 도저히 감도 오지 않는다. 아무튼 체스는 그 search space의 크기가 20년 전의 (슈퍼) 컴퓨터로 exact tree search가 가능할 정도의 크기였고 지금은 개인 PC에서도 exact search가 가능할 정도이나, 바둑은 그와는 비교도 할 수 없는 무시무시한 크기를 보여주는 것이다. (정확히는 약 googol배는 더 크다고 한다. 맞다, 구글의 이름의 기원인 세상에서 가장 큰 단위인 그 구골이다..) 때문에 AI 쪽에서는 바둑을 정복하는 것이 최대 과제 중 하나였다. 어떻게 이 어마어마한 search space를 감당할 수 있을것인가?

보다 더 자세한 설명을 하기 이전에, 바둑, 체스, 체커 등의 턴제 게임을 어떻게 tree search로 해결한다는 것인지 설명을 하고 넘어가도록 하자. 모든 턴제 게임은 일종의 트리 travel로 생각할 수 있다. 즉, 맨 처음 시작에서 각자가 한 턴을 소비할 때마다 트리의 노드로 이동하고, 결국 맨 마지막에 누군가가 승리하는 위치로 도달하면 게임이 끝나는 것이다. 체스는 그것이 체크메이크가 되는 것이고, 바둑은 돌을 더 이상 둘 곳이 없을 때 집의 개수가 더 많은 쪽이 되는 것이다. 특히 바둑에서는 tree가 다음처럼 표현된다.

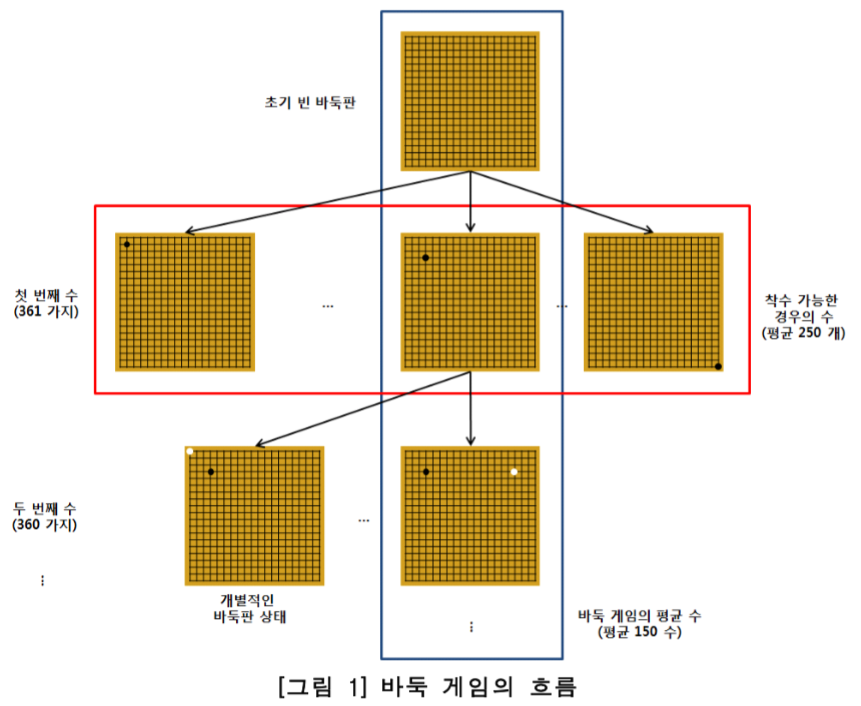
바둑의 Search Tree. 출처: [3]

그럼 이제 tree를 만들었으니, 매 순간마다 맨 끝까지 tree를 진행한다음 제일 좋은 결과를 보이는 node를 고르면 된다. 끝! …이라고 하고 싶지만 계속 반복해서 언급했듯 tree size가 우주 원자보다 많기 때문에 brute force는 불가능하다. 모 IT 변호사님 말처럼 모든 경우의 수를 세는 brute force를 하기 때문에 불공평하다는 얘기는 말이 안되는 셈. 때문에 알파고에서 가장 핵심이 되는 부분 중 하나는 바로 어떻게 tree search를 하느냐이다. Exact search가 힘들기 때문에 search space를 줄이는 적절한 approximation algorithm을 사용해야하는데 그 방법을 어떤 것을 취하는지가 문제가 되는 것이다.

이건 사족인데, 방금 위에서 얼렁뚱땅 대충 tree로 좋은 node를 고른다고 했지만, 사실은 Minimax algorithm이라는 것을 사용해서, 나의 이득은 최대화하고, 상대방의 이득은 최소화하는 방향을 계속 반복하면서 아래로 value를 propagate하면서 계속 sub tree를 만들고… 뭐 그런 알고리즘을 써야한다. 결국 모든 node에 저런 계산을 해야하기 때문에 바둑같은 무식하게 큰 tree에서는 이 방법을 쓸 수 없는 것이 문제가 되는 것. Minimax에 대해서는 한국어로 된 좋은 자료 [3]가 있으니 참고하면 좋다.

Monte-Carlo Tree search

바둑의 search space의 크기는 착수 가능한 경우의 수를 밑으로하고 250의 평균 바둑 한 판의 길이인 150수를 지수로 하는 무식하게 큰 숫자이다. 따라서 search space를 줄이기 위해서는 (1) tree의 breadth search를 줄이는 방법 (착수 위치를 exact하게 전부 고려하는 대신, 좀 더 작은 숫자로 줄이는 방법), (2) tree의 depth를 줄이는 방법 (매 번 tree를 exact하게 끝까지 보지않는 방법) 이 두 가지가 필요하다. 현재 (AlphaGo이전의) state-of-art 바둑 system들은 이 방법을 해결하기 위하여 Monte-Carlo Tree search (MCTS)라는 방법을 사용하고 있다. MCTS의 이름에 Monte-Carlo가 들어가는 것을 보면 알 수 있듯, 이 방법론은 tree search를 exact tree traversal을 하는 대신, random하게 node를 하나 고르고 (sampling하고) 그것을 통해 확률적인 방법으로 approximate tree search를 하는 방법론이다. 당연히 계속 반복하면 asymptotic하게 optimal value function으로 converge하는 것 역시 증명되어있다.

MCTS를 완전 high level로만 설명하면, 다음과 그림과 같은 4개의 seqeunce를 계속 반복하는 과정이라 할 수 있다.

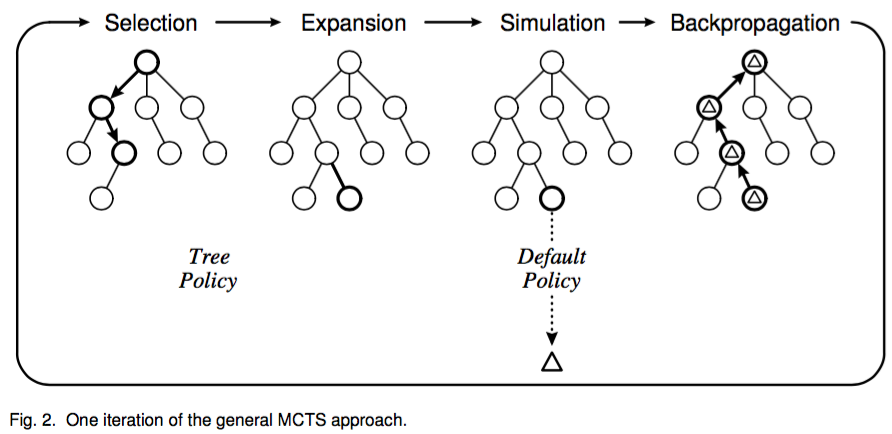
High level description of MCTS. 출처: [4]

각 step에 대한 설명은 다음과 같다. 여기에서 핵심은 Tree Policy, 그리고 Default Policy이다.

Selection: root node에서부터 __Tree Policy (child selection policy)__를 recursive하게 적용해서 leaf node L까지 도달한 후 L을 select한다.
Expansion: 만약 도달한 leaf L이 terminate state가 아니라면 (즉 L에서 게임이 끝나지 않았다면) __Tree Policy (leaf create policy)__에 의해 새로운 child node 한 개 혹은 여러 개를 더 만들어서 tree를 exapnd한다.
Simulation: 새 node 에서 __Default Policy__에 따른 outcome을 계산한다.
Backpropagation: Simulation 결과를 사용해 selection에서 사용하는 statistic들을 update한다.

이때 Tree Policy와 Default Policy에 대한 설명은 각각 다음과 같다.

Tree Policy: 이미 존재하는 search tree에서 leaf node를 select하거나 create하는 policy
- 바둑의 경우에는 특정 시점에서 가능한 모든 수 중에서 가장 승률이 높은 수를 예측하는 policy라고 생각하면 된다.
Default Policy: 주어진 non-terminal state에서의 (얼마나 좋은 state인지를 측정하는) value를 estimation을 하는 policy
- 바둑의 경우에는 현재 상황에서 얼마나 승리할 수 있을지를 measure하는 policy라고 생각하면 된다.

Backpropagation step 자체는 둘 중 어떤 policy도 사용하지 않지만, 대신 backpropagation을 통해 각 policy들의 parameter들이 update된다. 이 4개의 step이 한 iteration으로, MCTS는 시간이 허락하는 한도 내에서 이 과정을 계속 반복하고, 그 중에서 가장 좋은 결과를 자신의 다음 action으로 삼는다. 다음은 가장 ‘좋은’ node를 고르는 criteria의 4가지 예시이다.

Max child: 가장 높은 reward 값을 가지고 있는 node를 고른다.
Robust child: root node에서부터 가장 많이 visit된 node를 고른다.
Max-Robust child: 1, 2를 동시에 만족하는 node를 고르며, 그런 node가 없다면 계속 반복해서 그런 node를 찾아낸다.
Secure node: 가장 lower confidence bound를 maximize하는 node를 고른다.

딥마인드에서 쓴 논문 [1]이나 포스트 [2]를 보면 single machine과 multi machine에서의 성능 차이에 대해 언급하는데, 아마도 iteration을 더 많이 시도해볼 수 있기 때문에 결과가 더 좋은 것이 아닐까싶다.

MCTS의 일반적인 알고리즘을 정리하면 다음과 같이 적을 수 있다. (1) Tree Policy, (2) Default Policy, (3) Best Child Selection 이 세가지를 어떻게 정하느냐에 따라서 알고리즘의 종류가 바뀐다고 보면 된다.

알고리즘을 보면 알 수 있듯, 굉장히 reinforcement learning스러운 방식을 취하기 때문에 (1) Aheuristic, 즉 뭔가 이유가 있고 reasonable한 decision making을 할 수 있으며 (2) Asymmetric, 아래 그림처럼 tree를 symmetric하지 않게, 더 relevant한 부분만 집중적으로 서치할 수 있다.

Survey paper [4]를 보면 MCTS family 중에서 몇 가지 유명한 알고리즘들에 대해 설명하고 있는데 bandit 기반의 알고리즘들이 많이 있다. UCB를 기반으로 한 UCT (Upper Confidence Bounds for Trees), 그것을 좀 발전시킨 BAST (Bandit Algorithm for Smooth Trees).. 그것 이외에도 정말 수 많은 family들에 대해 설명하고 있으니 더 관심이 있으면 해당 논문을 읽어보면 좋을 것 같고, survey paper가 너무 길다면, MCTS에 대해 잘 정리되어있는 사이트 [5]가 있으니 이 사이트를 참고하면 좋겠다.

Approaches by AlphaGo

앞서 설명한 MCTS가 비록 full search를 하지 않아도 된다지만, 결국 바둑에 적용하기 위해서는 breadth와 depth를 줄이는 과정이 필요하다. AlphaGo에서 이 둘을 줄이기 위하여 사용한 것이 바로 deep learning technique으로, 먼저 착수하는 지점을 평가하기 위한 value network, 그리고 샘플링을 하는 distribution을 만들기 위한 policy network 두 가지 network를 사용하게 된다.

결국 AlphaGo가 한 것을 한 마디로 요약하자면 Monte-Carlo Tree search이며, tree의 search space를 줄이기 위하여 value network와 policy network 두 가지 (사실은 세 가지) network를 한 번에 learning할 수 있는 architecture를 만들고 이를 사용해 MCTS의 성능을 끌어올린 것이다. 따라서 이 방법은 비단 바둑에서만 사용할 수 있는 방법이 아니라, MCTS를 사용할 수 있는 거의 모든 방법론에 적용하는 것이 가능하다. 지금 AlphaGo가 input으로 흰 돌과 검은 돌들이 놓여져 있는 바둑판 그림을 사용하고 있기에 바둑을 학습하는 것이고, 그 이외에 search space가 너무 넓어서 exact tree search가 불가능한 model에서 전부 AlphaGo의 방법론을 사용할 수 있는 것이다.

다시 본론으로 돌아와서, 더 자세한 설명을 하기 이전에 먼저 General MCTS에서 사용하는 네 가지 step (selection, expansion, simulation, backpropagation)을 AlphaGo는 어떻게 적용했는지 살펴보자.

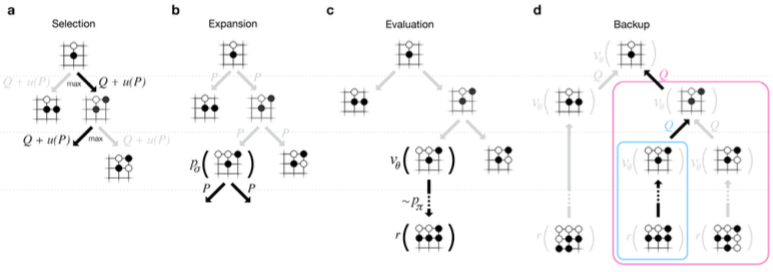
Selection: 현재 상태에서 Q + u가 가장 큰 지점을 고른다.
- Q: MCTS의 action-value 값, 클 수록 승리 확률이 높아짐 (Q function에 대해서는 이전에 쓴 reinforcement 글 [8] 참고)
- u(P): __Policy network (SL)__과 node 방문 횟수 등에 의해 결정되는 값
Expansion: 방문 횟수가 40회가 넘는 경우 child를 하나 expand한다.
Simulation: __Value network__와 __Fast rollout__이라는 두 가지 방법을 사용해 reward를 계산한다.
- Value network는 __Policy network (RL)__을 사용해서 learning한다.
Backpropagation: 시작 지점부터 마지막 leaf node까지 모든 edge의 parameter를 갱신한다.
1-4를 (시간이 허락하는 한도 내에서) 계속 반복하다가, Best Child Selection으로는 robust child, 즉 가장 많이 방문한 node를 선택한다.

AlphaGo는 위에서 언급한 policy network를 supervised learning (SL), reinforcement learning (RL) 두 가지로 나눠서 학습한다. SL network는 그 동안 실제 프로기사가 둔 기보를 바탕으로 특정 기보에 대한 다음 수를 classification하는 방식으로 learning하고, RL network는 SL network로 initialize한 후, reinforcement learning 방식 (AlphaGo의 자가대국이라고 부르는 방식)으로 주어진 기보에 대한 다음 수의 distribution을 학습한다.

AlphaGo는 앞에서 설명한 Rollout Policy, SL network, RL network 그리고 마지막 value network를 한 번에 pipeline 방식으로 learning하는 architecture를 디자인했다.

Supervised Learning of Policy Network (SL Policy Network)

먼저 AlphaGo의 Supervised Learning (SL) Policy Network $p_\sigma (a | s)$에 대해 알아보자. 이 네트워크는 단순한 CNN으로, input은 시간 t일 때의 기보(s)이고, output은 시간 t+1 일 때의 기보(a)가 된다. 따라서 이 네트워크는 classification network가 된다. 다만 문제라면 output layer의 dimension이 너무 거대하다는 것. 개인적으로 이런 도대체 네트워크를 어떻게 learning시킨건지 상상조차 되지 않는다. 참고로 이 네트워크는 단순 classification task만 하기 때문에 sequencial할 필요는 없다. 때문에 그냥 모든 (s,a) pair에서 랜덤하게 데이터를 샘플해서 SGD로 learning하게 된다.

네트워크는 총 13 layer CNN을 사용했으며 KGS라는 곳에서 3천만건의 기보 데이터를 가져와서 학습했다고 한다. 네트워크 구조를 어떻게 만들었는지 궁금해서 살펴보니, inner product layer는 하나도 없이 처음부터 끝까지 convolution layer만 학습한 모양이다.

논문에 따르면, AlphaGo는 이 부분에서 기존 state-of-art였던 44.4%보다 훨씬 좋은 classification accuracy인 57%까지 성능개선을 보였다고 한다. 또한 이 accuarcy가 좋으면 좋을수록 AlphaGo의 최종 winning rate가 상승한다는 사실까지 다음 그림과 같이 실험적으로 보이고 있다.

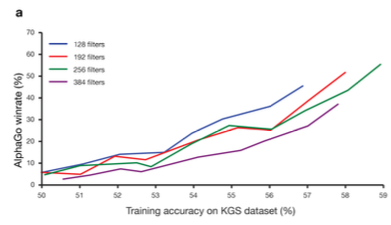
Reinforcement Learning of Policy Networks (RL Policy Network)

RL network는 SL network와 동일한 구조를 가지고 있으며, 초기 값 $\rho$ 역시 SL network의 parameter value $\sigma$로 초기화된다. RL network는 현재 RL network policy $p_\rho$와 이전 iteration에서 사용했던 policy network 중에서 랜덤하게 하나를 뽑은 다음 이 둘끼리 서로 대국을 하게 한 후, 둘 중에서 현재 네트워크가 최종적으로 이기면 reward를 +1, 지면 -1을 주도록 디자인되어있다. 그러나 당연히 그 reward는 대국이 끝난 시점의 T에서의 reward이지 현재 시점 t에서의 reward는 0이기 때문에, 대신 네트워크의 outcome을 $z_t = \pm r(s_T)$으로 정의한다. 즉, 이 네트워크의 outcome은 현재 player의 time t에서의 terminated reward가 된다. 이 네트워크 역시 Stochasic gradient method를 사용해 expected reward를 maximize하는 방식으로 학습이 된다. 여기에서 과거에 학습된 네트워크를 사용하는 이유는, 좀 더 generalize된 모델을 만들고, overfitting을 피하고 싶기 때문이라고 한다 (언론에서 말하는 ‘자기 자신이랑 계속 반복해서 대국을 진행하는 방식으로 더 똑똑해진다’ 라는 표현은 여기에서 나오는 자가 대국을 의미하는 것 같다).

논문에 따르면 SL policy network와 RL policy network가 경쟁할 경우, 거의 80% 이상의 게임을 RL network가 승리했다고 한다. 또한 다른 state-of-art 프로그램들과 붙었을 때도 훨씬 좋은 성능을 발휘했다고 한다.

Reinforcement Learning of Value Networks

이제 AlphaGo의 deep learning architecture 중에서 마지막 단계인 value network $v_\theta (s)$만 남았다. Value network는 evaluation 단계에서 사용하는 네트워크로, position (현재 기보) s와 policy p가 주어졌을 때, value function $v^p(s)$를 predict하는 네트워크이다. 즉, 다음과 같은 식으로 표현할 수 있다.

$$v^p(s) = \mathbb E [z_t | s_t = s, a_{t\ldots T} \sim p].$$

문제는 그 누구도 바둑에서 최적의 수를 모르기 때문에 (다시 강조하지만 search space가 우주의 원자 개수보다 많다) optimal value function $v^*(s)$를 학습할 방법이 없다는 것이다. 그 대신, AlphaGo는 현재 시스템에서 가장 우수한 policy인 RL policy network $p_\rho$를 사용해 optimal value function을 approximation한다. Value network는 앞에서 설명한 policy network와 비슷한 구조를 띄고 있지만, 마지막 output layer으로 모든 기보가 아닌, single probability distribution을 사용한다. 따라서 이제 문제는 classification이 아니라 regression이 된다. Value network는 현재 가장 state-outcome pair인 (s,z)에 의해서 학습이 된다 (여기에서 z는 RL network에서 나왔던 최종 reward의 값으로 1 또는 -1이다).

따라서 Value network는 s에 대해 z가 나오도록 하는 regression network를 학습하게 되며, error는 $z - v_\theta(s)$가 된다. 그런데 문제는, state s는 한 개의 기보인데, reward target은 전체 game에 대해 정의되므로, succesive position들끼리 서로 강하게 correlation이 생겨서 결국 overfitting이 발생한다는 것이다. 이 문제를 해결하기 위해 AlphaGo는 3천만개의 데이터를 RL policy network들끼리의 자가대국을 통해 만들어낸 다음 그 결과를 다시 또 value network를 learning하는 데에 사용한다. 그 결과 원래 training error 0.19, test error 0.37로 overfitted되었던 네트워크가, training error 0.226, test error 0.234로 훨씬 더 generalized된 네트워크로 학습되었다는 것을 알 수 있다.

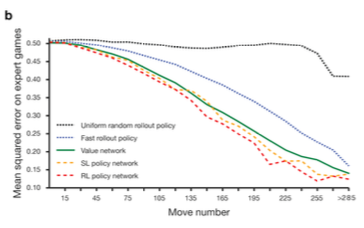
마지막으로, 아래 그림은 랜덤 policy, fast rollout policy, value network, SL network 그리고 RL network를 사용했을 때 각각의 value network의 expected loss가 plot되어있다. Loss는 실제 프로기사가 둔 수와, 각 policy로 둔 수와의 mean square loss이다. 결국, RL policy를 쓰는 것이 그렇지 않은 것보다 훨씬 우수한 결과를 낸다는 것을 알 수 있다.

이제 high level로 앞에서 살펴본 세 네트워크를 살펴보자.

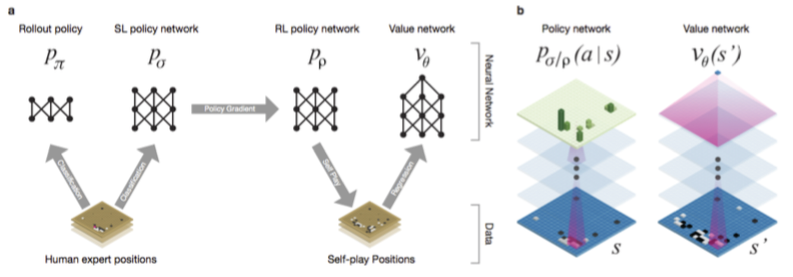
먼저 왼쪽 그림은 어떻게 AlphaGo에서 세 네트워크를 pipeline 형태로 묶었는지를 보여준다. 사람이 실제로 둔 기보를 바탕으로 rollout policy, SL policy를 learning하고, SL policy를 initialization 값으로 사용해 RL policy를 learning한다. 그 후 RL policy를 사용해 value network를 learning하는 것이다.

앞에서 깜빡하고 언급하지 않았는데, Fast Rollout Policy는 전체 바둑 상태가 아닌 local한 3 by 3 판에서 다음 수를 빠르게 예측해서 terminate state까지 게임을 play한 후 simulation하는 policy로, policy network를 사용한 방법보다 성능은 떨어질지 몰라도 약 1500배 정도 빠르다고 언급되고 있다. 그냥 빠른 naive approach라고 생각하면 될 것 같다.

오른쪽 그림에서는 policy network와 value network의 차이를 보여주고 있다. Policy network들은 전부 input, output이 기보로 나타나고 (input이 지금 기보, output이 다음 기보) value network는 board 전체에 대한 probability를 학습한다는 점이 다르다. 즉, policy network는 주어진 기보에서 가장 확률이 높은 action을 고르는 방식으로 MCTS의 selection을 하는 역할을 하고, value network는 simulation결과를 통해 실제로 둘 수 있는 점들 중에서 가장 이길 확률이 높은 (reward가 승리이므로) 곳을 찾아내는 역할을 하게 되는 것이다.

그리고 [3]에서 구체적인 CNN 구조를 설명한 그림이 있어서 인용하도록 하겠다.

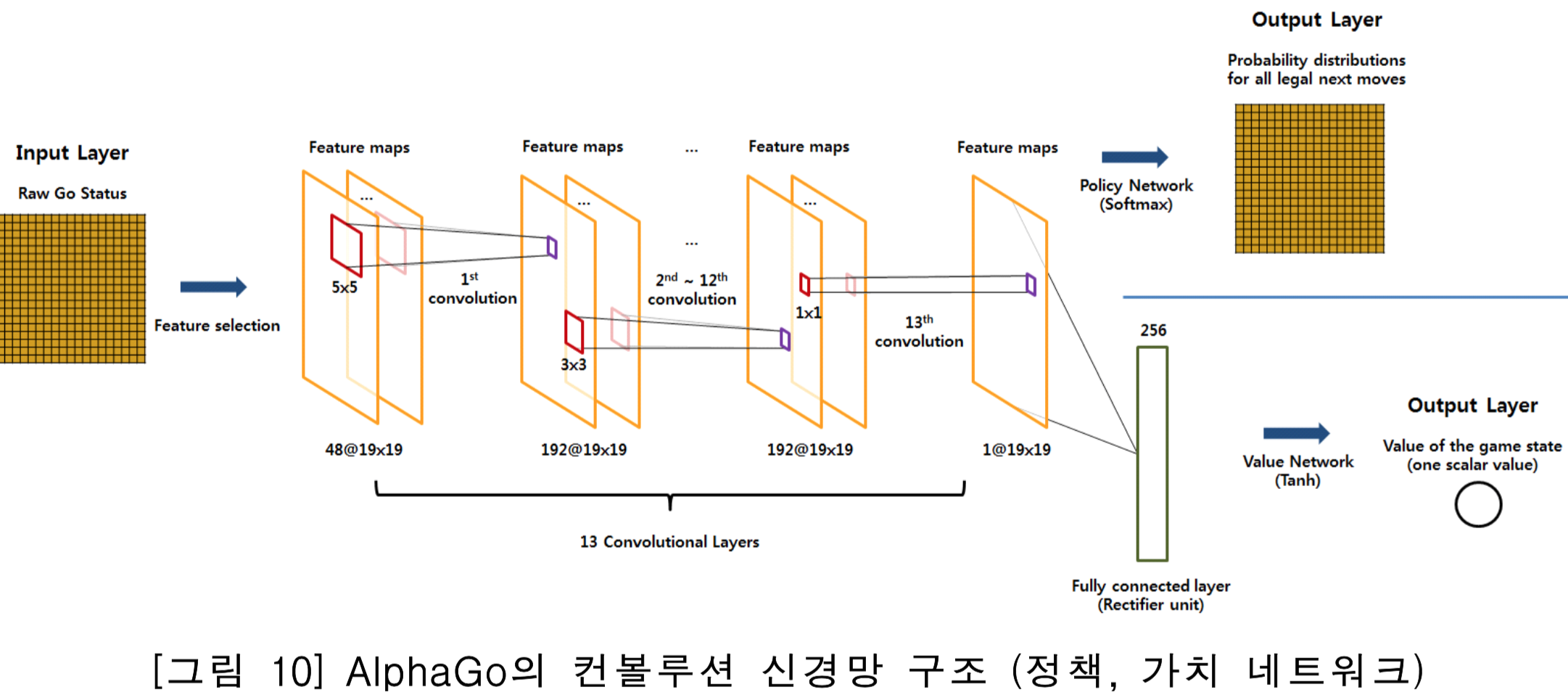
Searching with Policy and Value Networks

이제 policy와 value network를 설계하였으니 실제로 이 네트워크들을 어떻게 MCTS에서 사용하는지 살펴보자. MCTS의 각각의 edge (s,a)는 action value Q(s,a), visit count N(s,a), prior probability P(s,a)를 저장한다. Tree는 simulation을 사용해서 traversal을 root node에서부터 진행하게 된다. Simulation의 각 step t마다, action $a_t$는 state $s_t$에 대해 다음과 같이 정의된다.

$$a_t = \arg\max_a (Q(s_t,a) + u(s_t, a)), \mbox{ where } u(s,a) \propto \frac{P(s,a)}{1+N(s,a)}. $$

Traversal을 지속하다 leaf node L에 도달하게 되면, expand여부를 결정하게 된다 (방문횟수로 결정하는 듯 하다). 그 후 leaf node에서의 position $s_L$을 사용해서 SL policy $p_\sigma$를 prior P에 저장한다. 즉, $P(s,a) = p_\sigma(s,a)$가 된다. 이때 leaf node는 두 가지 방법으로 evaluate된다. 먼저 value network $v_\theta(s_L)$, 그리고 fast rollout policy $p_\pi$를 사용해 terminal step T까지 도달했을 때 random rollout play로 얻어진 outcome $z_L$. 이 둘은 parameter $\lambda$를 사용해 다음과 같이 combine된다.

$$ V(s_L) = (1-\lambda)v_\theta (s_L) + \lambda z_L. $$

앞에서 진행한 simulation이 끝나고나면, 이제 각 edge들이 가지고 있는 parameter들을 update할 차례다. 앞에서 언급했듯, AlphaGo의 MCTS는 각각의 edge (s,a)에 action value Q(s,a), visit count N(s,a), prior probability P(s,a)를 저장한다. 여기에서 P(s,a)는 SL network로 update가 되고, 남은건 Q와 N이다. 이 값들은 다음과 같은 과정으로 업데이트 된다.

$$N(s,a) = \sum_i \mathbf{1}(s,a,i)$$

$$Q(s,a) = \sum_i \frac{1}{N(s,a)} \mathbf{1}(s,a,i) V(s_L^i).$$

$s_L^i$는 i번째 simulation에서 leaf node를 의미하며, $\mathbf{1}(s,a,i)$는 i번째 simulation에서 edge (s,a)가 관측되었는지에 대한 indicator function이다. 이런 방식을 통해 서치가 다 끝나고나면 AlphaGo는 root에서 부터 가장많이 선택된 node를 선택하는 방식으로 한 수를 둔다.

재미있는 점은, MCTS의 policy function으로 SL policy를 쓰는 것이 RL policy보다 낫다고 논문에 report된 점이다. 이유는 (SL policy를 learning할 때 사용한) 사람이 두는 수는 뒤를 생각한 좀 더 global한 수를 두는 반면, RL policy는 그 순간의 가장 최고의 move를 하기 때문에, SL policy가 더 낫다는 것이다. 반면, value network는 SL network가 아닌 RL network를 사용하는 편이 훨씬 성능이 좋다고 한다.

정리

이 글에서는 자세한 네트워크의 구조나 코드 구현보다는 실제로 이 알고리즘이 어떻게 동작하는지, 그리고 모델은 어떻게 구성했는지에 대해 집중적으로 다뤘다. AlphaGo는 MCTS를 deep learning pipeline을 통해 훨씬 성능을 개선한 work이라 할 수 있으며, network는 SL, RL 두개의 policy network 그리고 value network 총 세 가지를 learning하게 된다. Policy network는 MCTS의 selection에서 쓰이게 되며, value network는 MCTS의 evaluation에서 쓰이게 된다.

각종 매체나 언론에서는 알파고가 인간이 1000년 동안 두어야 둘 수 있는 대국을 진행했고, 최적의 수를 항상 찾아내기 때문에 이세돌 사범에게 불리하다는 식으로 보도를 하고 있지만, 사실은 그 이전에도 AlphaGo가 사용하던 데이터와 동일한 데이터로 훨씬 못한 결과들을 내왔었다. 결국 알파고가 뛰어난 점은 기존 방법들보다 훨씬 smart한 architecture를 디자인하고, 그 architecture의 power를 최대한으로 끌어올리기 위해서 parallel computing 등의 각종 기법들을 사용해서 시스템을 엄청 정교하게 만들었다는 점이라고 할 수 있다. 그러나 아무리 대단한 시스템 엔지니어라고 하더라도, 근본이 되는 모델의 성능이 나쁘다면 그 시스템을 인간 수준으로 끌어올리지는 못했을 것이다. 결국 구글은, 그리고 딥마인드는, 정말 ‘인간답게’ sequencial decision process를 학습하는 멋진 시스템을 디자인했다고 볼 수 있을 것 같다.

References

변경 이력

2016년 3월 15일: 글 등록