Coursera강의를 들은지 한참이 지난 줄 알았는데 고작 1주일 밖에 되지 않았다. 아무튼 까먹기 전에 처음 얘기했던대로 하나하나 차근차근 블로그에 정리를 해볼까 한다.

Linear Regression

지난 Post에서는 간단하게 supervise learning과 unsupervise learning에 대해서 언급했다. 이제 supervise learning 중 linear regression에 대해서 얘기를 해보자. 개인적으로는 regression을 하기 이전에 baysian을 설명하는 것을 선호하지만, 그건 그냥 다음 포스트에 설명하기로 하고 (Andrew Ng 교수는 Coursera강의에서 Baysian을 따로 수업으로 다루지 않았다.) 먼저 regression부터 살펴보자.

Linear regression을 가장 간단하게 설명하자면 Excel의 추세선과 거의 비슷한 개념이라고 생각하면 된다. 즉, 지금 내가 가지고 있는 데이터셋이 어떤 Linear function인지를 유추하는 것이다. 간단한 예시를 보자. 아래 그래프를 공부시간과 시험성적의 그래프라고 생각해보자. (가로축을 공부 시간 세로축을 시험성적)

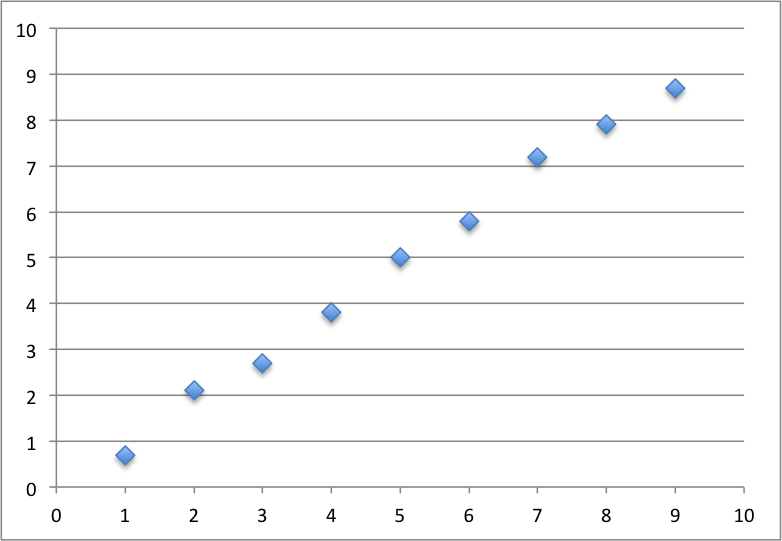
이 그래프는 대체로 1차 함수(linear function)의 꼴을 가지고 있다는 것을 알 수 있다. 그렇다면 아마도 4.5의 공부 시간을 투자한 학생은 약 4.5 정도의 시험성적을 받을 것이라고 예측할 수 있지 않을까?

물론 현실에서 공부 시간과 성적이 선형 비례하지는 않지만, 아무튼 이런 예시를 통해서 우리는 이 System이 가지고 있는 일종의 특성을 예측할 수 있다. 이때 우리가 ‘데이터가 x일 때 y의 결과가 나올 것이다’ 라고 예측한 둘 사이의 관계 혹은 함수를 hypothesis라 한다. 이 부분은 지난 포스트에서 설명한 부분이니 자세한 설명은 넘어가도록 하겠다. 그렇다면 특정 데이터셋이 들어왔을 때 hypothesis는 어떻게 도출할 수 있을까? 아래 그래프를 보자

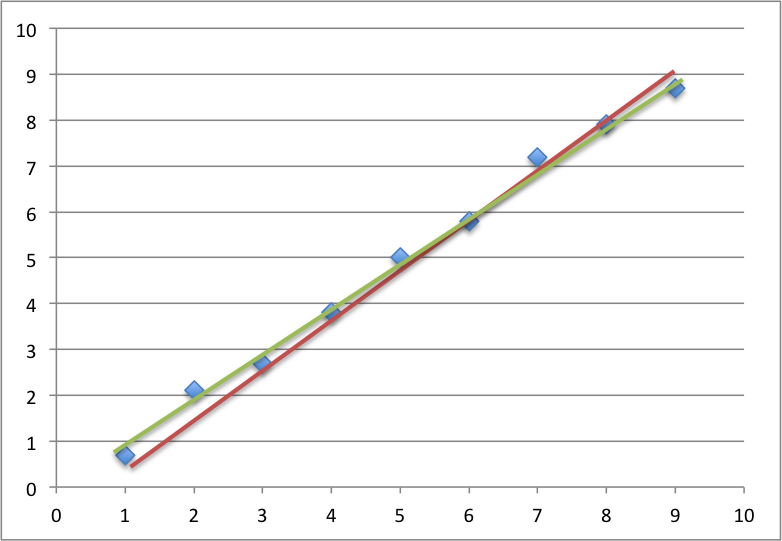
빨간 선과 초록 선 중 어느 hypothesis가 더 좋다고 할 수 있을까? 사람이 선택하는 것은 언제나 부정확하다. 때문에 우리는 수식적으로, 정확하게 scoring할 수 있는 무언가를 원하는데 그 이유로 우리는 Loss Function을 필요로 한다.

Loss Function

이 hypothesis가 좋은 hypothesis인지 아닌지 어떻게 알 수 있을까? 사실 답은 간단하다. ‘새로운 데이터의 결과를 얼마나 잘 예측을 하느냐’. 하지만 새로운 데이터가 없이는 Scoring이 불가능하다. (온전히 불가능한 것은 아니고 model selection을 통해 validation을 하는 skill이 있다. 하지만 지금 포스트의 주제는 아니기 때문에 나중에 설명하도록 하겠다.) 때문에 지금 존재하고 있는 데이터에서 찾은 패턴이 전체 패턴과 동일하다는 가정하에 지금 데이터에 얼마나 잘 fit하느냐로 Scoring을 하는 것이 가능할 것이다. 즉, 새로운 데이터를 이용하여 Scoring을 해야하지만, 새로운 데이터를 받기 이전에 Scoring을 하고 그 hypothesis를 사용해야하기 때문에 지금 가지고 있는 dataset이 향후 새로 들어올 데이터와 유사하다고 생각하고 지금 가지고 있는 값을 이용해 fitting을 하는 것이다.

이때 사용하는 것이 바로 Loss function이다. Hypothesis의 Loss를 측정하여 그 값을 최소화 하는 것이다. Loss 혹은 Cost라는 이름에서 유추할 수 있듯 이 값은 function으로 예측된 (predicted) 값과 측정된 (observed) 값의 차이를 사용하여 계산한 값이다. 여러가지 Loss function의 꼴이 있는데, 가장 간단하게 사용할 수 있는 function은 (data_p - data_o)^2이다. data_p는 이 hypothesis를 사용하여 예측한 값이고 data_o는 실제 관측 결과 얻은 값이다. 그 밖에 0-1 Loss라고 해서 값이 정확하게 일치하면 0, 아니라면 1 만큼의 Loss를 가지는 매우 Strict한 Loss function이다. 이후에 설명하게 될 classfication에서 간혹 쓰인다.

Gradient Descent

이제 이 Loss function이 가장 작은 값을 가지는 hypothesis를 선택하면 된다. 그렇다면 그 값은 어떻게 찾을 것인가? 여러가지 방법이 있지만, 일반적으로는 Gradient Desent라는 방법을 사용한다. Gradient descent란 쉽게 생각하면 긿을 잃은 상태에서 산을 내려가는 방법이라고 생각하면 된다. 산을 가장 빠르게 내려가기 위해서는 아마 현재 내가 서있는 지점에서 가장 경사가 가파른 지점을 향해서 내려가고, 움직인 위치에서 다시 한번 경사가 가장 가파른 지점을 향해서 내려가고.. 이 과정을 반복하다보면 언젠가 가장 낮은 지점으로 이동할 수 있을 것이다. 이제 이 개념을 머리에 넣어두고 아래 그림을 보자.

출처: http://www.mathworks.com/matlabcentral/fx_files/27631/1/fff.png

위의 그림에서 볼 수 있듯 가장 경사가 가파른 지점을 따라 내려 걸어가다보면 가장 낮은 지점으로 도달할 수 있을 것이다. 그런데 여기에서 문제가 하나 발생한다. 만약에 Initial Condition이 작은 봉우리가 아니라 반대쪽 높은 봉우리였다면? 그렇다면 우리는 아마 Global minimum, 즉 전체에서 가장 낮은 지점이 아닌 Local minimum, 즉 주변에서 가장 낮은 지점으로 이동하게 될 것이다. 전체에서 가장 작은 값과 그 주변에서 가장 작은 값을 선택하는 것은 분명 큰 차이가 있다. 하지만 이런 단점에도 불구하고 gradient descent는 매우 많이 쓰이는 방법 중 하나이다. 그 이유는 (1) 구현이 쉽고, (2) 모든 차원 및 공간으로 확대가 가능하다 라는 이유가 있다. Gradient descent는 또한 내가 속도를 조절할 수 있다. 산을 내려갈 때 얼마나 움직인 다음 방향을 바꿀 것인가에 따라 수렴 속도가 급격하게 변한다. 너무 그 폭이 작으면 시간이 너무 오래걸리고, 폭이 너무 크면 최악의 경우에 한 지점에 수렴하지 못할 수도 있다. 그 뿐 아니라 경우에 따라서는 gradient descent가 끝이 나지 않을 수도 있다. 하지만 여러 방법으로 그 단점들을 보완할 수 있고 무엇보다 아래 코드에서도 확인할 수 있듯 구현이 너무 간단하기 때문에 상당히 많이 쓰이는 방법이다. 더 자세한 것은 Wikipedia page를 참고하면 좋은 정보가 많다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# From calculation, we expect that the local minimum occurs at x=9/4

x_old = 0
x_new = 6 # The algorithm starts at x=6
eps = 0.01 # step size
precision = 0.00001

def f_prime(x):
    return 4 * x**3 - 9 * x**2

while abs(x_new - x_old) > precision:
    x_old = x_new
    x_new = x_old - eps * f_prime(x_old)
print "Local minimum occurs at ", x_new

출처: http://en.wikipedia.org/wiki/Gradient_descent#A_computational_example

Overfitting

이제 적절한 hypothesis를 찾기 위하여 loss function의 최소점을 gradient descent로 찾을 수 있다. 이제 더 이상 우리가 고민할 것은 없어보인다. 아니, 사실 그렇지 않다. 앞서 가정한 바에 의하면, 우리는 지금 존재하는 데이터셋이 전체 데이터셋의 분포를 대변한다고 가정했다. 하지만 꼭 그러리라는 보장을 할 수 있을까? 당연히 없다. 우리가 보고 있는 자료가 엄청 큰 패턴 중에서 매우 일부의 예외일 수도 있고, 혹은 노이즈 때문에, 너무 샘플 수가 적어서 잘못된 방향으로 pattern을 찾게 될 수도 있다. 이런 경우를 일컬어 Overfitting이라고 한다. 즉, 기존의 데이터에만 너무 충실해서 새로운 데이터가 들어왔을 때 도저히 써먹을 수가 없는 상태를 일컬어 Overfitting이라 한다. 이 것을 해결하기 위하여 여러가지 방법이 있는데 Model Selection과 Regularization이 그것이다. 이에 대해서는 다음 포스트에서 다루고자 한다.

Linear Regression은 매우 간단한 supervise learning의 예시이지만 상당히 중요한 개념들에 대해서 많이 다뤄야 한다. 특히 Loss function은 정말 중요하고 그 Loss function을 계산하는 gradient descent도 너무 중요하고, 마지막에 잠시 언급한 Overfitting은 너무 중요하다 못해 머리가 아플 정도다. 아직 정말 중요한 부분들을 일부 설명 못했지만 Overfitting에서 할 얘기가 너무 많아서 이쯤에서 줄여야겠다.

참고도서

Bishop, Pattern Recognition and Machine Learning

Simon Rogers, A First Course in Machine Learning

Stephen Marsland, Machine Learning: An Algorithmic Perspective