README   SanghyukChun's Blog

Practical Bayesian Optimization of Machine Learning Algorithms (NIPS 2012)

| Comments

들어가며

Machine Learning 모델을 만들다보면 Hyperparameter 라는 녀석을 다뤄야 하는 일이 종종 발생한다. 예를 들면 Random forest의 forest 개수라거나, Neural network의 layer 개수, learning rate, momentum 값 등등.. 문제는 이런 hyperparameter들을 어떻게 설정하느냐에 따라 그 결과가 크게 바뀌기 때문에 소위 말하는 ‘튜닝’에 시간을 매우 많이 쏟아야한다는 점이다.

이 논문은 hyperparameter tuning 문제를 Bayesian optimization을 사용해여 해결하는 방법을 제안한다. Bayesian optimization은 알려지지 않은 “black-box” function을 optimization할 때 많이 사용되는 방법이다. 그러나 Bayesian optimization은 몇 가지 이유로 practical하게 쓰기 어려운데, 1) (kernel function, acquisition function 등) 모델을 어떤 것을 고르냐에 따라 성능이 크게 바뀐다, 2) Baysian optimization 자체도 hyperparameter가 있어서 이 hyperparameter들을 튜닝해야한다, 3) Sequential update를 해야하기 때문에 parallelization이 되지 않는다 등의 이슈가 있다.

이 논문은 1) empirical하게 좋은 성능을 보이는 적절한 kernel function과 acquisition function을 제안하고, 2) Baysian optimization의 hyperparameter를 (MCMC로 풀 수 있는) fully baysian approach를 통해 전체 optimization에서 한 번에 계산할 수 있는 방법을 제안할 뿐 아니라, 3) MCMC를 사용해 풀 수 있는 theoretically tractable parallelized Bayesian optimization을 제안한다.

사실 이 논문을 제대로 이해하기 위해서는 아래 개념들에 대해 이미 잘 알고 있어야한다.

  • Stochastic process (Random process라고도 부른다)
  • Gaussian process (GP) & kernel function of GP
  • Bayesian optimization & acquisition function
  • Markov chain Monte Carlo (MCMC)

마지막 MCMC는 이 글에서는 다루지 않기로 하고, 나머지들에 대해서는 차근차근 정리하면서 내용을 진행해보도록 하겠다.

Hyperparameter Tuning as Optimization Problem

보통 hyperparameter를 찾기 위해 사용되는 방법들로는 Grid search, Random search 등의 방법들이 있다. Random forest 모델 하나를 예로 들어서 위 방법들에 대해 자세히 살펴보자.

Random forest에서 사용하는 hyperparameter는, tree의 개수 (n_estimators), split criteria (criterion), max depth (max_depth), leaf 당 최소 샘플 개수 (min_samples_leaf), … 등등이 있다. (자세한건 Scikit learn의 Random Forest 코드 참고)

우리가 찾고 싶은 hyperparameter는,

1
2
3
4

n_estimators = [10, 50, 100, 200]
criterion = ['gini', 'entropy']
max_depth = [None, 100, 10]
min_samples_leaf = [1, 5, 10, 20]

의 조합 중에 하나라고 가정해보자.

먼저 Grid search는 모든 parameter의 경우의 수에 대해 cross-validation 결과가 가장 좋은 parameter를 고르는 방법이다. 즉, 위에 나열된 hyperparameter의 모든 가능한 경우의 수는 4 x 2 x 3 x 4 = 96개인데, 모든 96개의 parameter들에 대해서 training data를 80:20으로 나누어 (꼭 80:20일 필요는 없다) 80으로 train을 하고, 20으로 test을 했을 때, test 결과가 제일 좋은 parameter를 고르는 것이다.

이 방법은, 주어진 공간 내에서 가장 좋은 결과를 얻을 수 있다는 장점이 있지만, 시간이 정말 정말 오래걸린다는 단점이 존재한다. 또한, 예시에서도 볼 수 있었듯, parameter의 candidate을 늘릴 때 마다 그 만큼의 시간이 더 필요하기 때문에, 정해진 시간 안에 parameter를 찾기 위해서는 어쩔 수 없이 hyperparameter의 candidate을 더 늘리지 못하고, candidate set이 제한된다는 단점이 존재한다.

이런 단점을 피하기 위해 나온 방법이 바로 random search이다. Random search는 모든 grid를 전부 search하는 대신, random하게 일부의 parameter들만 관측한 후, 그 중에서 가장 좋은 parameter를 고른다. Bengio 연구팀이 2012년에 발표한 논문 2에 따르면, high dimensional hyperparameter optimization에서는, grid search를 하는 것 보다, random search를 했을 때 성능이 더 좋을 수 있다고 주장하고 있다.

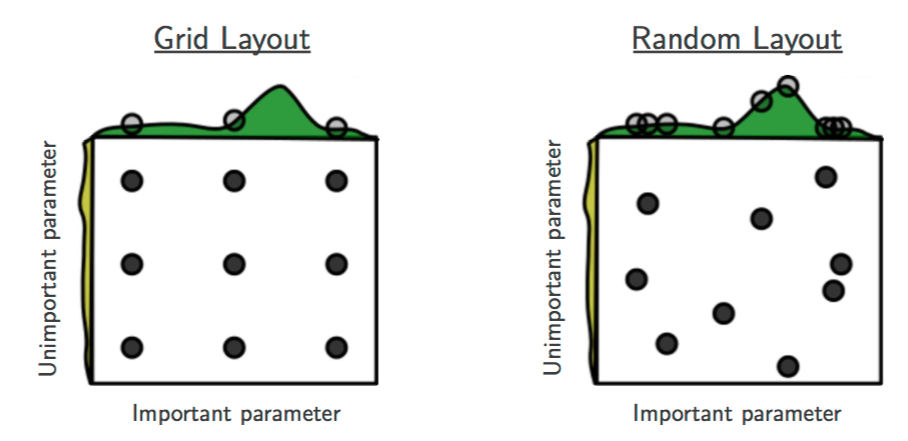
서로 importance가 다른 두 개의 parameter가 있다고 가정해보자. Grid search는 중요하지 않은 parameter와 중요한 parameter를 동일하게 관측해야하기 때문에 정작 중요한 parameter를 다양하게 시도해볼 수 있는 기회가 적지만, random search는 grid로 제한되지 않기 때문에 확률적으로 중요한 parameter를 더 살펴볼 수 있는 기회를 더 받게 된다. 출처: [2]

Machine Learning에서 hyperparameter search가 어려운 이유 중 하나는, hyperparameter가 바뀔 때 마다 모델이 바뀌게 되므로 다시 모델을 새로 learning해야한다는 점이다. 만약 실험 하나하나가 시간이 엄청 오래걸린다면, full grid search를 시도하기는 어려울 것이다. 그렇기에 random search가 꽤 유용하게 사용될 수 있는 여지가 더 많고, 실제로 나도 hyperparameter를 튜닝해야겠다싶으면 random search를 사용한다. (Scikit learn에서도 관련 패키지를 제공한다.)

Grid search와 random search의 좋은 점 중 하나는, 모든 trial들이 independent하므로 parallelization이 자연스럽게 이루어진다는 점이다.

Bayesian Optimization for “Black-box” function

Bayesian optimization은 다음과 같은 아주 무난한 optimization을 푸는 방법론 중 하나이다.

이때, $X$는 bounded domain이고, $f(x)$는 그 모양을 모르는, 즉 input을 넣었을 때 output이 무엇인지만 알 수 있는 black box function이라 가정하자. Optimization에는 여러 form이 있지만, minimization을 다루는 것이 일반적이기 때문에 여기에서도 minimization 꼴을 사용하도록 하겠다. Bayesian optimization은 $f(x)$가 expensive black-box function일 때, 즉 한 번 input을 넣어서 output을 확인하는 것 자체가 cost가 많이 드는 function일 때 많이 사용하는 optimization method이다.

Bayesian optimization은 다음과 같은 방식으로 작동한다.

  1. 먼저 지금까지 관측된 데이터들 $D = [(x1, f(x1)), (x2, f(x2)), \ldots]$ 를 통해, 전체 function f(x)를 어떤 방식을 사용해 estimate한다.
  2. Function f(x)를 더 정밀하게 예측하기 위해 다음으로 관측할 지점 $(x{n+1}, f(x{n+1}))$ 을 어떤 decision rule을 통해 선택한다.
  3. 새로 관측한 $(x{n+1}, f(x{n+1}))$ 을 $D$에 추가하고, 적절한 stopping criteria에 도달할 때 까지 다시 1로 돌아가 반복한다.

1에서 언급한 estimation을 할 때에는 $f(x)$가 Gaussian process prior를 가진다고 가정한 다음, posterior를 계산하여 function을 estimate한다. 2에서는 acquisition function $a(x | D)$를 디자인해서 $\arg\max_x a(x | D)$ 를 계산해 다음 지점을 고른다.

간단한 예시를 통해서 이게 무슨 말인지 조금 더 자세히 살펴보자.

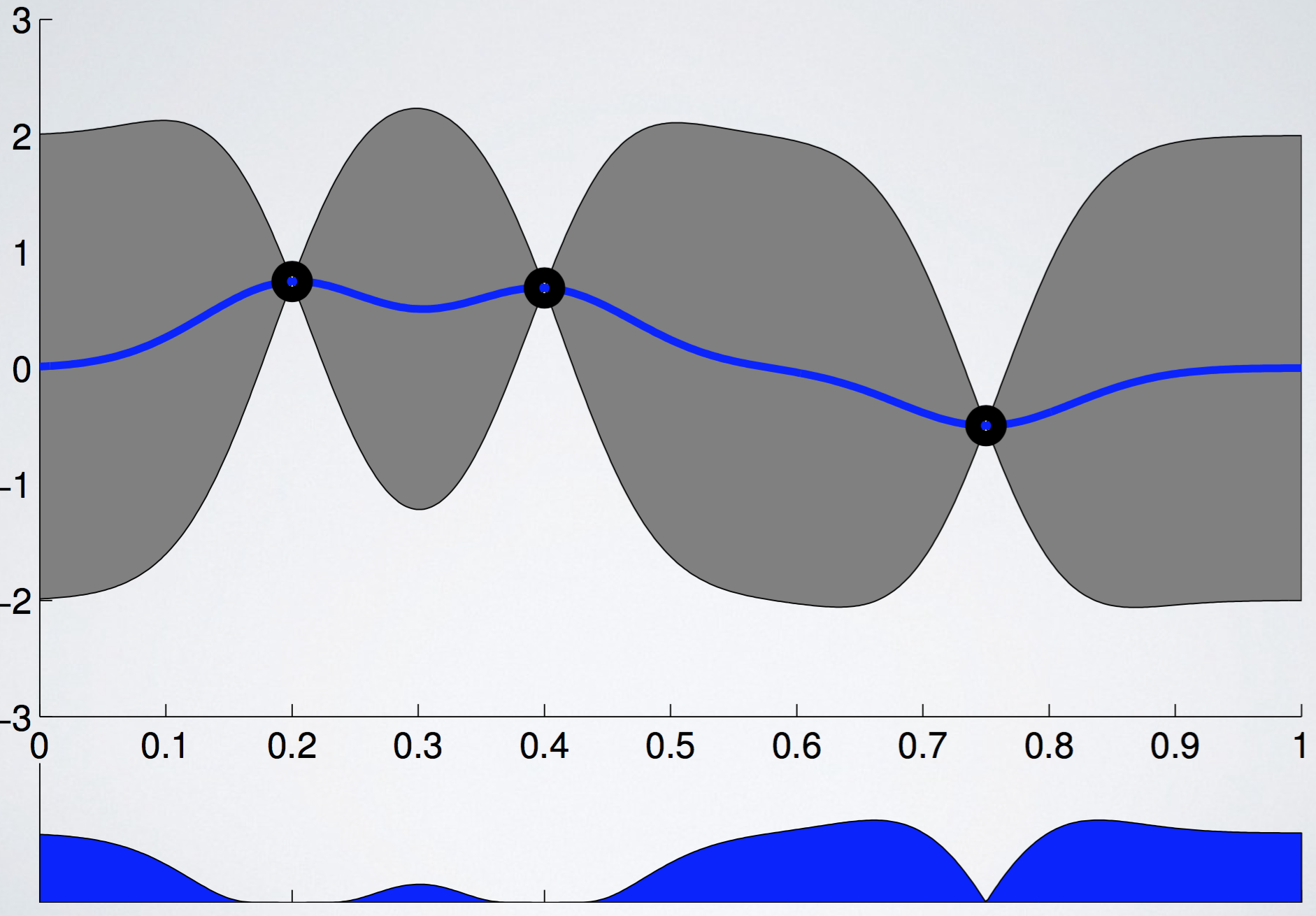
아래 그림에서 빨간색 점선은 우리가 찾으려고 하는 unknown black box function $f(x)$ 를 나타내고, 까만색 실선은 지금까지 관측한 데이터를 바탕으로 우리가 예측한 estimated function $\widehat f(x)$ 의 expectation을 의미한다. 까만선 주변에 있는 회색 영역은, function f(x)가 존재할 confidence bound이고 (쉽게 말해서 function의 variance이다), 밑에 있는 $EI(x)$는 위에서 언급한 acquisition function을 의미한다. (어떻게 구하는지는 아직 신경쓰지 말자) 출처: [3]

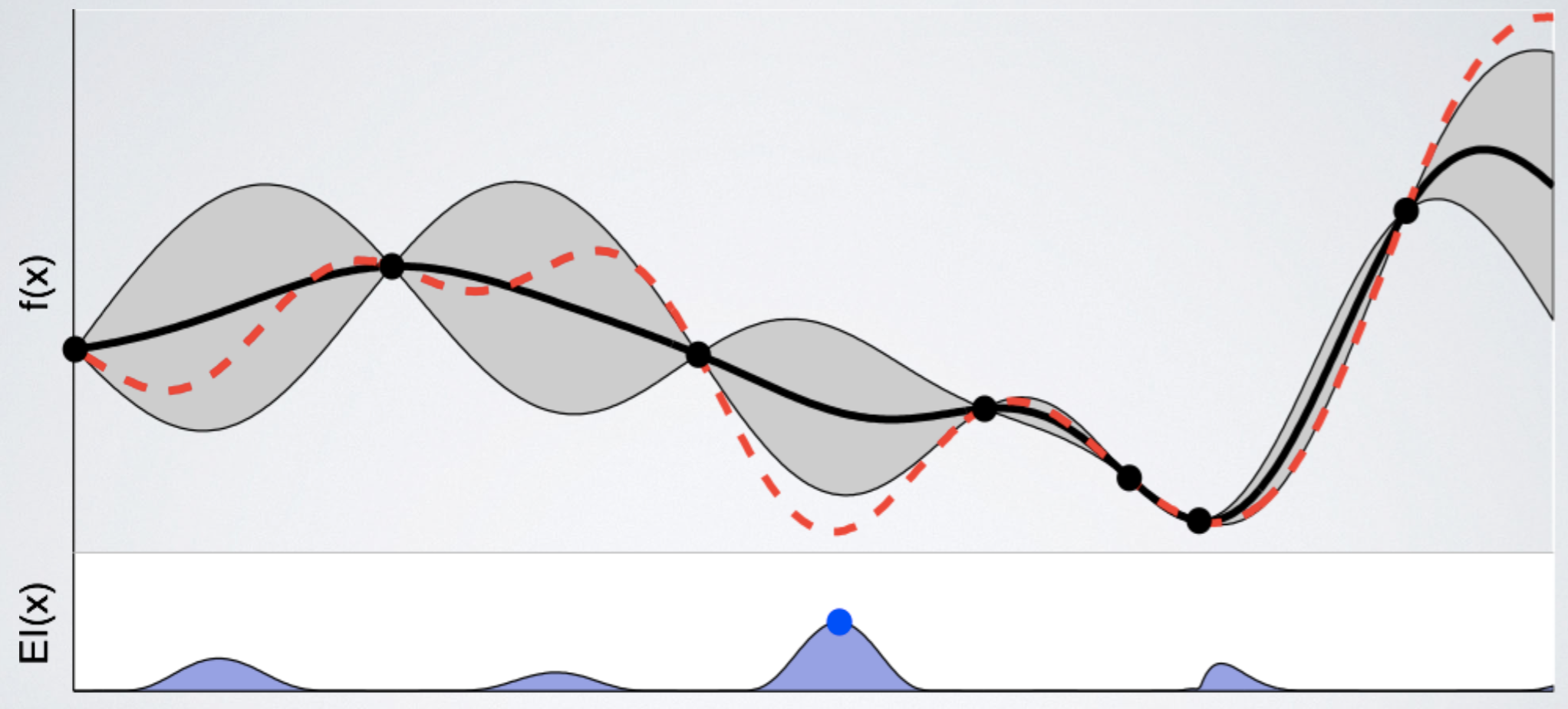지금까지 관측한 데이터를 바탕으로, (acquisition function 값이 제일 큰) 파란색 점이 찍힌 부분을 관측하는 것이 가장 좋다는 것을 알 수 있다.

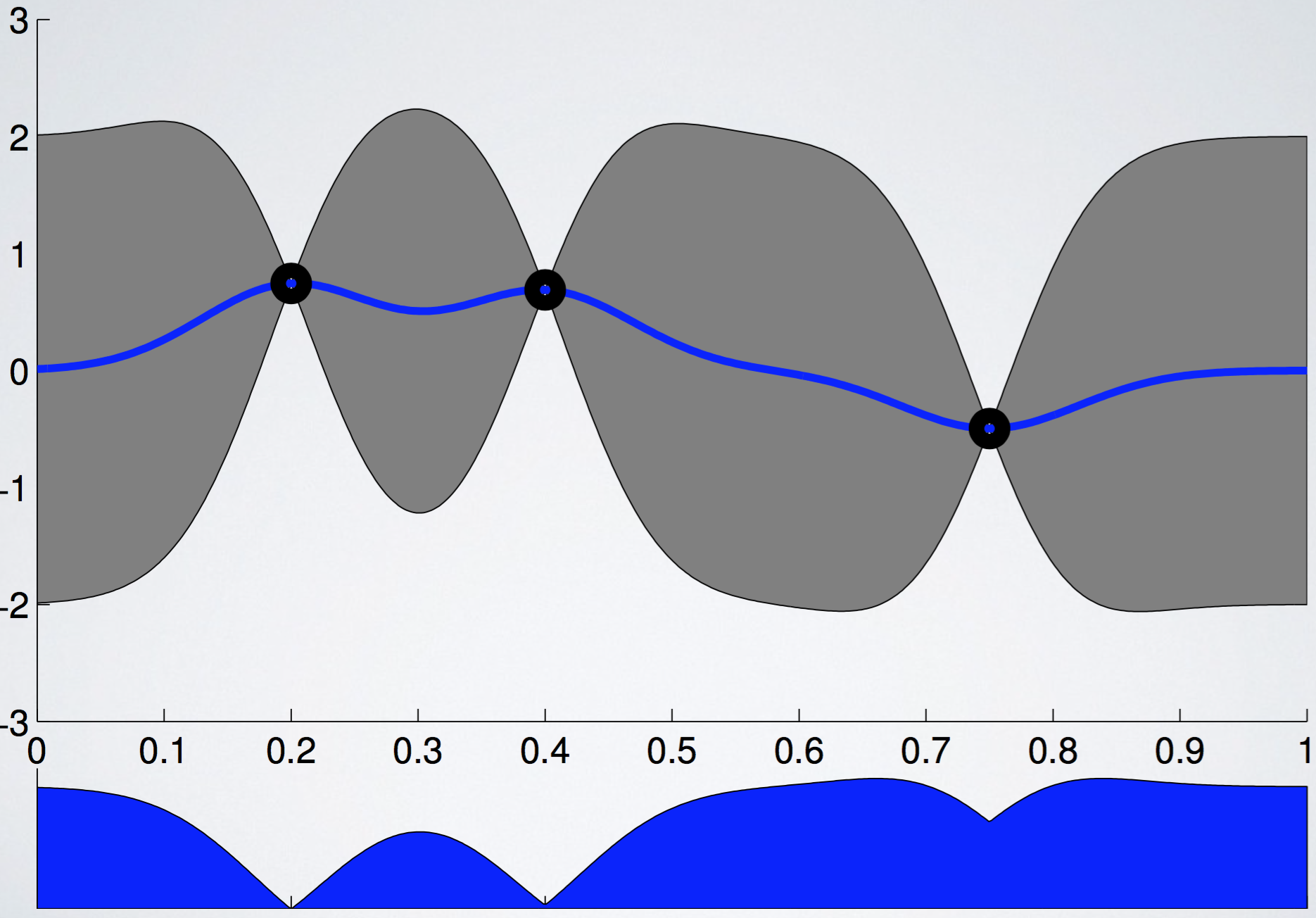
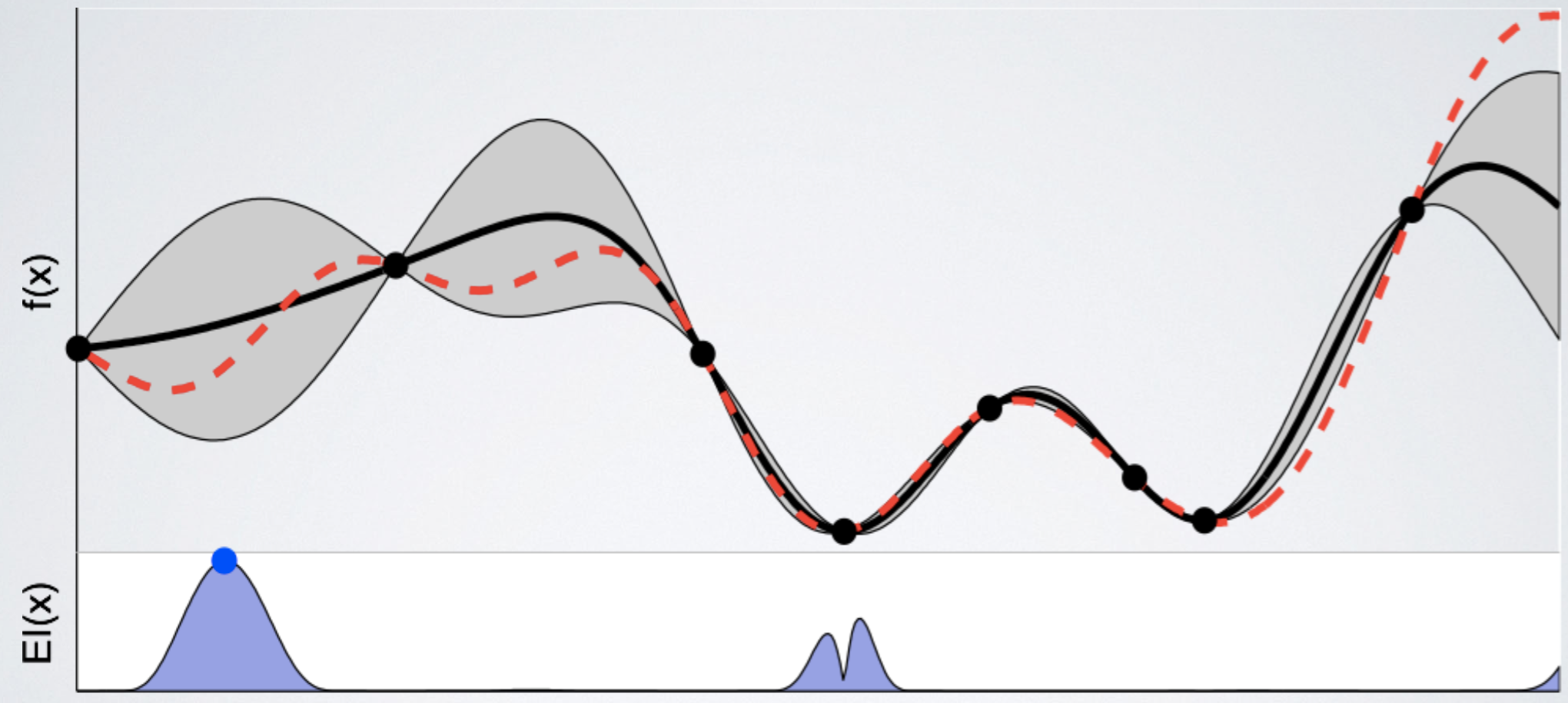위에서 acquisition function 값이 제일 컸던 지점의 function 값을 관측하고 estimatation을 update한다. 함수의 uncertainty를 의미하는 회색 영역이 크게 감소했음을 알 수 있다. 그러나 여전히 좌측 부분과 우측 부분의 uncertainty가 꽤 큼을 알 수 있다. 다시 한 번 다음 관측할 point를 acquisition function을 통해 고른다.

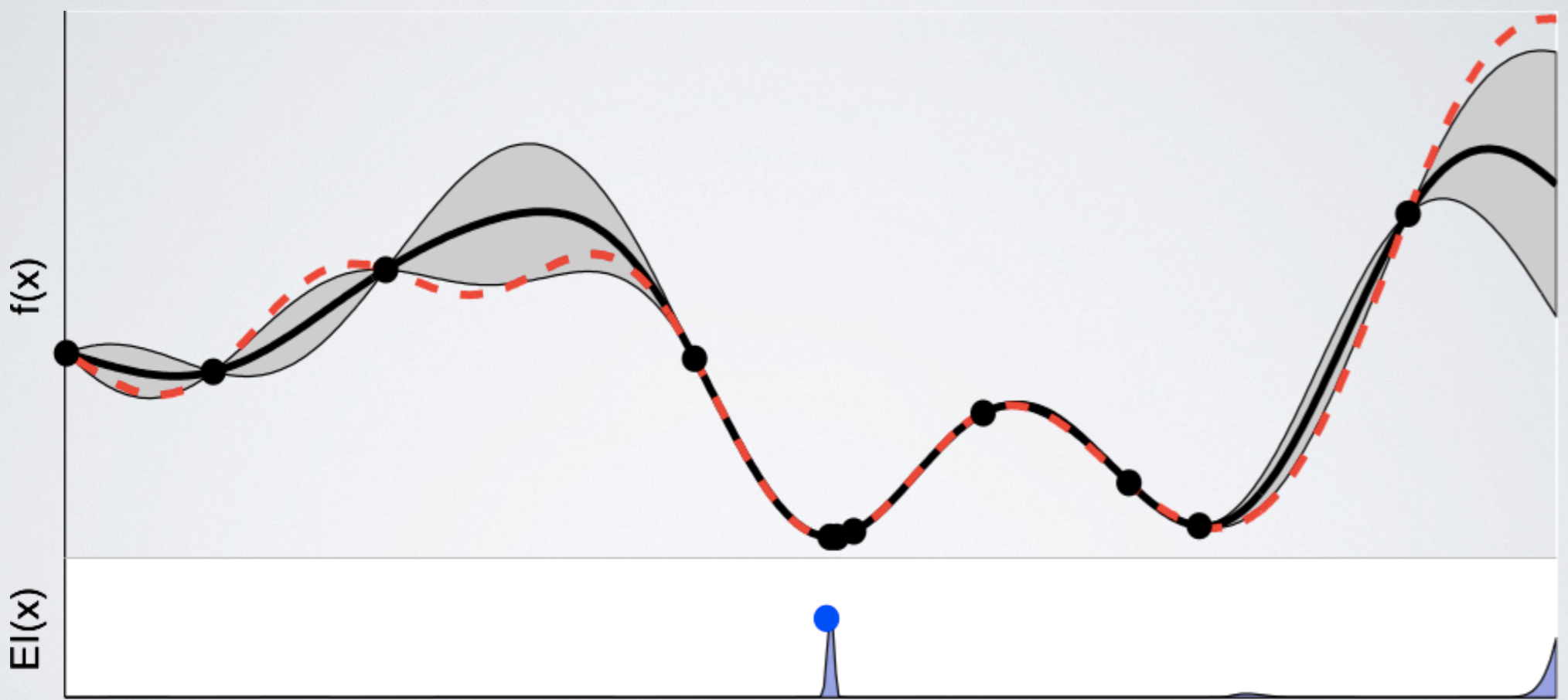계속 update를 진행한 결과, estimation과 실제 function이 거의 흡사해졌다. 이제 여태까지 관측한 지점 중 best point를 argmin f(x) 로 선택한다.

이것이 Bayesian optimization의 대략적인 procedure이다. 여기까지 설명한 내용은 완전히 새로운 것이 아니라, 오래 전에 이미 제안되었었고, 계속 쓰이던 방법이다. 이 내용을 완전히 이해하고 있어야 이 글에서 다루는 논문을 이해할 수 있다. 앞에서 Bayesian optimization을 위해서는 두 가지가 필요하다는 언급을 했었다. 하나는 function을 estimate하는 방법과, 또 하나는 다음 관측 지점을 고를 acquisition function이다. 이 두 가지 개념들이 대해 다음 두 subsection에서 조금 더 자세히 살펴보도록 하자.

Stochastic Process

Stochastic process가 무엇인지 설명하기에 앞서, Random variable이란 무엇인지 알고 있어야한다. 특히 ‘Random variable은 함수이다’ 라는 개념을 이해하고 있어야하는데, 이 개념에 대해 살펴보도록 하자.

Random variable은 probability space에서 어떤 real value R로 가는 function으로 정의가 된다. 이때 이 real value R이 pdf나 cdf를 의미하는 것이 아니라, random variable의 값 그 자체가 된다. Probability space란, 확률 값이 정의가 되는 공간이고, random variable이란 그 공간에서 실제 real value로 가는 function인 것이다.

주사위를 예로 들어보자. 먼저 주사위의 probability space는 {1, 2, 3, 4, 5, 6} 으로 정의가 되며, 각각의 값이 나올 확률은 동일하게 $Pr(X=1) = Pr(X=2) = \ldots = Pr(X=6) = 1/6$ 으로 정의가 된다. 여기에서 주사위의 random variable X는 다음과 같이 정의된다.

이 개념을 조금 더 확장시킨 것이 stochastic process이다. Stochastic process는 어떤 ordered set T로 indexed된 random variable들의 collection으로 정의된다.

Ordered set T는 보통 시간이나 공간 등의 개념과 대응된다. Stochastic process라는 것 자체가, 시간에 따른 어떤 값의 변화를 추정하기 위해 도입된 개념이다보니, (자그마치 아인슈타인이 브라운 운동 증명할 때 썼던 개념이라고 한다) 일반적으로는 이 ordered set은 시간으로 생각해도 충분하다. 앞서 설명한 random variable의 collection을 조금 더 간단하게 이야기하면, stochastic process는 probability space와 시간 T에 대한 function이라고 생각할 수 있다. 즉, 똑같은 probability space에서 한 지점을 sample했을 때, random varible은 값이 나오고 (주사위의 눈금이 나오고), stochastic process는 t에 대한 함수가 (random variable $X_t$가) 나오게 된다. 그림으로 보면 아래와 같다.

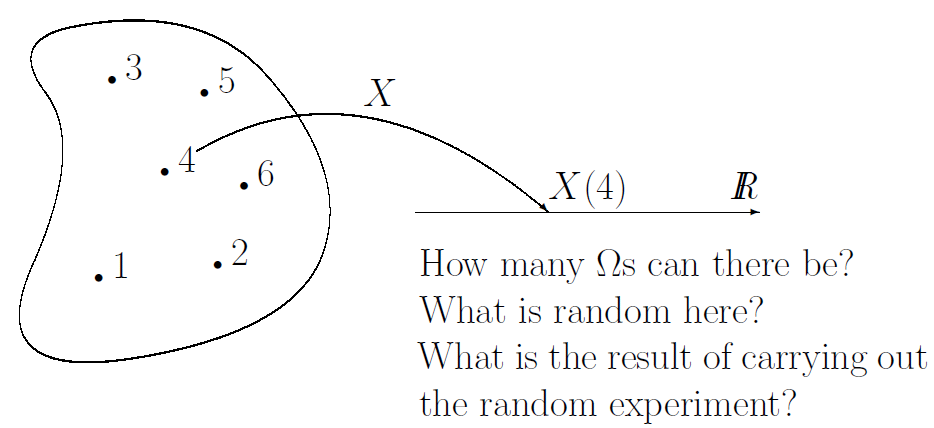
Random variable $X$에서 값을 sample하면 real value R을 가지는 특정 값을 얻게 된다. 즉, X는 probability space에서 R로 가는 함수라고 할 수 있다.

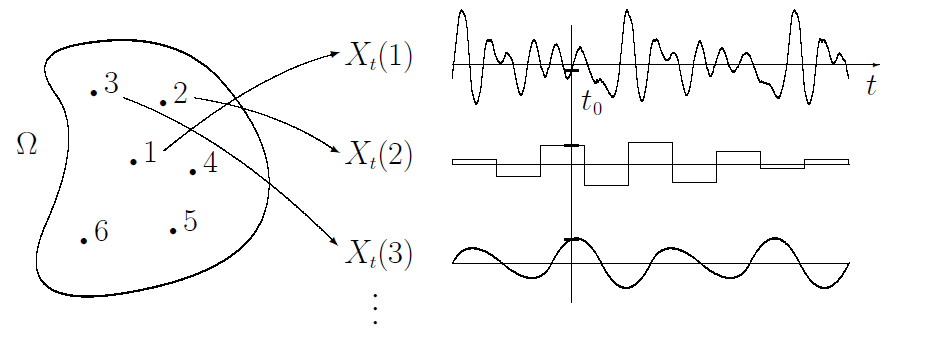
Stochastic process $X_t$에서 값을 sample하면 시간 t에 대한 서로 다른 함수를 얻게 된다. 즉, $X_t$는 probability space에서 다른 function space로 가는 함수라고 할 수 있다.

Random process와 stochastic process에 대한 (그리고 뒤에서 설명할 Gaussian process 역시) 조금 더 자세한 내용은 reference에 추가한 블로그 글 [4]을 참고하면 좋을 것 같다. (위 그림의 출처 역시 같은 블로그이다.)

Gaussian Process

Gaussian process, 줄여서 GP는 continuous domain에 대해 정의되는 statistical distribution이다. 이때, input domain에 있는 모든 point들은 normal distribution random variable이 되며, 아무 finite한 GP sample들을 뽑더라도, 그 sample들은 multivariate normal distribution을 가지게 된다.

GP의 개념은 이 정도로만 설명을 마무리하고, formulation에 대해 살펴보자. GP 하나를 정의하기 위해서는 mean function과 kernel function 두 가지 함수가 먼저 정의되어야 한다.

먼저 mean function $m(x)$는 이름에서도 쉽게 유추할 수 있듯 point x에서의 mean value를 나타내는 x에 대한 함수이다. 보통은 constant value m을 많이 선택하며, 그마저도 선택하지 않고 그냥 zero-mean을 고르는 경우도 많다고 한다.

Kernel function이 상당히 중요한데, kernel function은 주어진 GP sample들이 서로 어떤 relationship을 가지는지, 어떤 covariance matrix를 형성하게 되는지 정의하는 함수이다. Kernel function $k(x, x^\prime)$은 점 두 개에 대해 정의가 되는데, 일반적으로 점 사이의 거리가 가까우면 relationship이 크고, 멀먼 작을 것이라는 가정을 하게 된다. 가장 간단한 kernel function인 squared-exponential kernel function은 다음과 같다. 이때, $x_d$는 $x$의 d 차원 value이고, $\alpha, \theta_d$는 hyperparameter이다. ($\theta_d$는 1부터 D까지 총 D개 존재한다.)

Kernel function을 사용해 두 점 사이의 relation을 정의하고 나면, GP sample collection이 주어졌을 때, 해당 sample들의 covariance matrix를 다음과 같이 정의할 수 있다. 이 경우는 sample이 총 n개가 있고, $k_{ij} := k(x_i, x_j)$ 라고 정의하도록 하겠다.

Mean function $m(x)$와 kernel function $k(x, x^\prime)$이 정의가 되었으므로, 어떤 point x가 주어졌을 때, (앞에서 모든 GP의 sample은 normal ditribution r.v.라고 했음을 기억하자) 그 점의 mean과 variance를 계산할 수 있으므로, 이 둘만 정의가 된다면 아무 임의의 지점에 대해 Gaussian distribution r.v. 을 얻을 수 있다.

이 글에서는 function f(x)가 GP prior를 가진다고 가정했을 때, likelihood가 주어졌을 때 posterior가 어떻게 update되는지까지는 다루지 않을 것이다. 조금만 찾아보면 잘 정리된 내용들을 찾을 수 있을 것이다.

GP with Noisy data

모든 함수가 항상 deterministic output을 가지지는 않는다. 오히려 거의 대부분의 real world function들은 관측할 때 마다 그 값이 바뀌게 된다. 이를 보통 우리는 noise라는 현상으로 설명하고는 한다. 조금 더 formal하게 적어보자.

다음과 같은 observation pair ${x_i, y_i}$ 가 있다고 가정해보자. 이 값은, input $x_i$와, 그 때 관측된 함수값 $y_i$의 pair로, 만약 noise가 없다면 $y_i = f(x_i)$ 라고 바로 쓸 수 있지만, 대부분의 경우는 noise가 있어서 그렇게 표현할 수 없다. 가장 많이 쓰이는 방법은 white Gaussian noise를 추가하는 방법이다. 따라서 이런 경우에 y는 다음과 같이 표현된다.

이때, $\nu$는 noise의 세기를 나타내는 hyperparameter가 된다. 이렇게 표현할 경우, noise가 없을 때와 있을 때 GP를 fit한 결과는 아래와 같은 차이가 나게 된다.

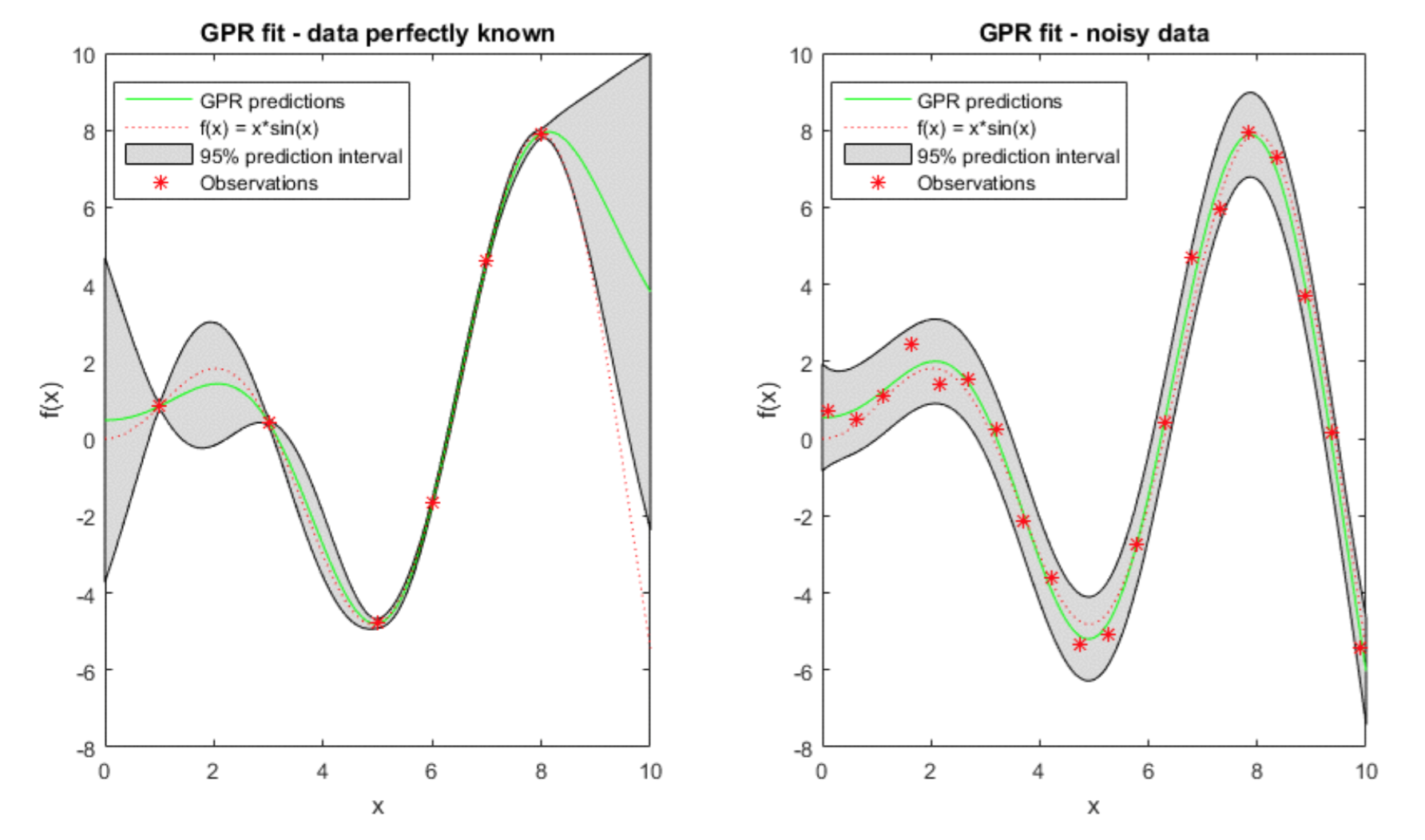
Acquisition Function

Function f(x)가 GP prior를 가지는 Bayesian optimization을 진행 중이라고 가정해보자. f(x)의 모든 point x에 대해, 우리는 mean과 variance를 계산할 수 있다 (위에 언급되었던 그림 중 까만 선과 회색 영역). 이때 다음으로 관측해야할 부분이 어디인지 어떻게 알 수 있을까?

한 가지 방법은 estimated mean의 값이 가장 작은 지점은 관측하여 현재까지 관측된 값들을 기준으로 가장 좋은 점을 찾아보는 것이다. 또 다른 방법은 variance의 값이 가장 큰 지점을 관측하여, 함수의 모양을 더 정교하게 탐색하는 방법이 있다. 즉, 다음에 어떤 점을 탐색하느냐를 결정하는 문제는 explore-exploit 문제가 된다. Explore는 high variance point를 관측하는 것, exploit은 low mean point를 관측하는 것이 되겠다. Acquisition function이란 explore와 exploit을 적절하게 균형을 잡아주는 역할을 하며, 여러 종류가 있지만, 여기에서는 세 가지만 다루도록 하겠다 (Probability of Improvement, Expected Improvement, UCB).

이 섹션의 남은 부분에서, $f^\prime$ 이란, 지금까지 관측한 function 값 중에서 가장 minimum 값을 지칭하도록 하겠다.

Probability of Improvement

Probability of improvement (PI)는, 특정 지점의 함수 값이 지금 best 함수 값인 f’ 보다 작을 확률을 사용한다. 즉, PI의 utility function은 다음과 같다.

Estimated function f(x)의 값은 정해진 값이 아니라 확률 값이기 때문에, PI는 x에서의 u(x)의 expectation으로 표현된다.

이때 $\mathcal N(f;\mu(x), k(x,x))$는 mean function $\mu(x)$와 kernel function $k(x, x)$로 표현되는 normal distribution이고, $\Phi(\cdot)$은 cdf를 의미한다. PI를 그림으로 나타내면 아래와 같다. 아래 그림에서 이미 explore가 많이 된 지점이 PI가 높은 것에 주목하라. (밑에 나올 그림들의 출처는 모두 [5] 이다.)

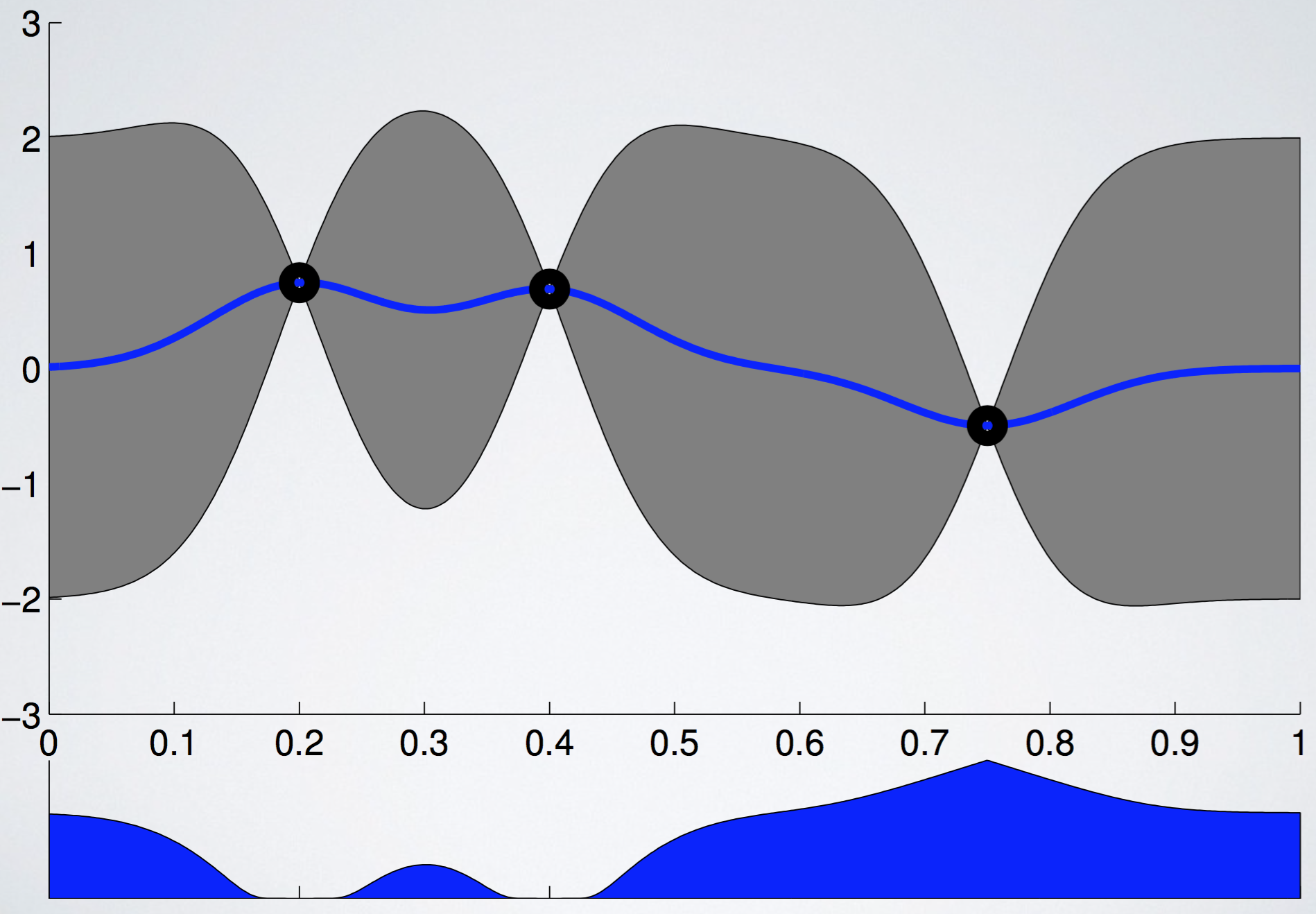
Expected Improvement

PI의 가장 큰 문제점 중 하나는, ‘improvement’ 될 수 있는 확률만 보기 때문에, 확률이 조금 더 낫을지라도, 궁극적으로는 더 큰 improvement가 가능한 point를 고를 수 없다는 점이다. 다시 말하면 exploit에 집중하느라 explore에 취약하다는 단점이 있다. Expected improvement (EI)는 utility function을 0, 1이 아니라, linear 꼴로 정의하기 때문에 그 차이를 반영할 수 있다. (Step function과 ReLU의 차이라고 보면 된다) EI의 utility function은 다음과 같다.

주의할 점은, EI가 PI의 expectation이 아니라는 점이다. 그냥 이름만 비슷한거고 완전히 다른 function이라고 생각하면 된다. PI와 마찬가지로 EI역시 u(x)의 expectation을 계산해야 한다.

EI를 그림으로 나타내면 다음과 같다. PI처럼 이미 explore가 많이 된 곳을 또 찾는 실수는 덜 저지른다는 것을 볼 수 있다.

UCB

UCB는 우리가 이미 잘 알고 있는 그 UCB이며, acquisition function은 다음과 같다.

UCB의 문제점이라면, explore-exploit trade-off parameter인 $\beta$의 존재이다. Form도 간단하고, 조절하기 쉽기도 하지만, hyperparameter를 또 조정해야한다는 문제 때문에 이 논문에서는 다루지 않는다. UCB 역시 그림으로 나타내면 다음과 같다.

이 이외에도 Entropy search, Thompson sampling 등의 다양한 acquisition function이 있지만 이 글에서는 다루지 않도록 하겠다.

Limitation of Bayesian Optimization

지금까지 Bayesian optimization (BO)에 대해 ‘간략히’ 알아봤다. 여기까지 글을 읽으면서 느꼈겠지만, Bayesian optimization은 굉장히 impractical하다. 여러가지 이유가 있는데, 크게는 다음과 같은 이유들이 있다.

  • Hyperparameter search를 하기 위해 BO를 사용하는데, BO를 사용하기 위해서는 GP의 hyperparameter들을 튜닝해야한다 (kernel function의 parameter 등)
  • 어떤 stochastic assumption을 하느냐에 따라 (어떤 kernel function을 사용해야할지 등) 결과가 천차만별로 바뀌는데, (model selection에 민감한데) 어떤 선택이 가장 좋은지에 대한 가이드가 전혀 없다.
  • Acquisition function을 사용해 다음 지점을 찾는 과정 자체가 sequential하기 때문에 grid search나 random search와는 다르게 parallelization이 불가능하다.
  • 위에 대한 문제점들이 전부 해결된다고 하더라도 software implementation이 쉽지 않다.

이런 문제점들을 해결하기 위해 이 논문은 (그렇다 이제서야 이 논문이 어떤 일을 했는지 얘기할 수 있게 되었다) 먼저 kernel function을 여러 실험적 결과 등을 통해 Matern 5/2 kernel이 가장 실험적으로 좋은 결과를 낸다는 결론을 내린다 (즉, kernel function은 언제나 Matern 5/2를 쓰면 된다). 또한 acquisition function도 EI로 고정한다. 다음으로 GP의 hyperparameter들을 Bayesian approach를 통해 acquisition function을 hyperparameter에 대해 marginalize한다. 이 marginalized acquisition function은 (integrated acquisition function이라고 한다) MCMC로 풀 수 있는데, 자세한 얘기는 뒤에서 이어서 하도록 하겠다. 마지막으로 이 논문은 이론적으로 tractable한 Bayesian optimization의 parallelized version을 (MCMC estimation이다) 제안한다.

저자들이 작성한 코드 역시 GitHub에 공개가 되어있다. (HIPS repo에 있는 코드가 최신이다. 둘이 라이센스가 다르기 때문에 상황에 맞춰 쓰면 된다.)

그 밖에도 최근 다른 곳에서도 이 내용을 implement한 것 같다.

Practical Bayesian Optimization

Expected Improvement and Matern 5/2 Kernel function

앞에서도 설명했듯, 이 논문은 먼저 acquisition function으로는 EI를 사용하고, kernel function으로는 Matern 5/2를 사용한다. Kernel function을 무엇을 고르냐에 따라 어떤 변화가 나타나는지 보여주는 좋은 그림이 하나 있어 첨부한다. 출처: [5]

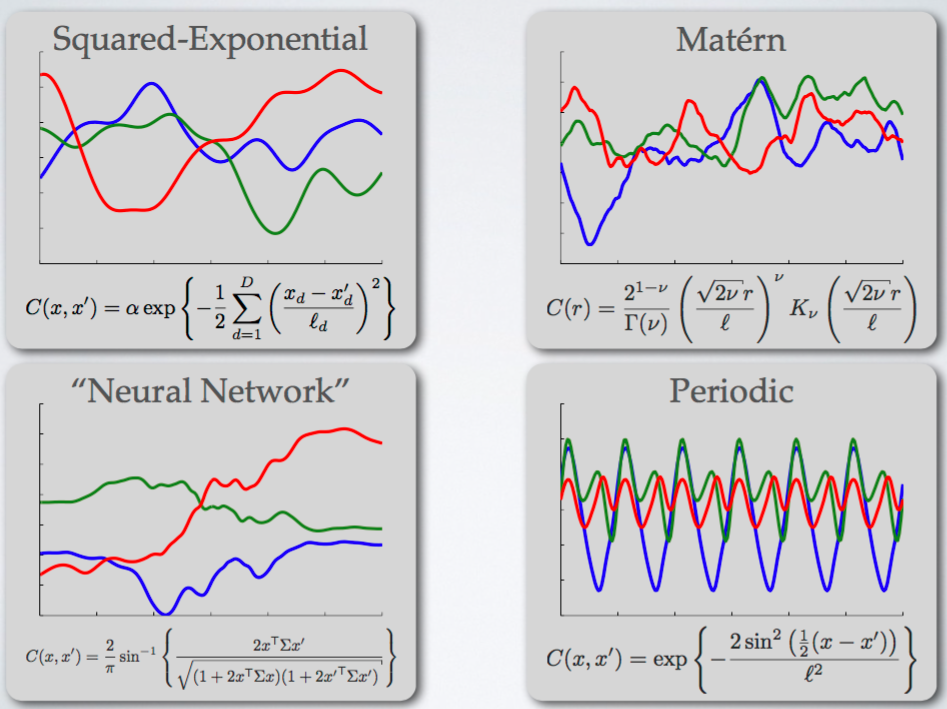
가장 많이 쓰이는 Squared-exponential function의 가장 큰 문제는 ‘smoothness’로, 복잡한 모델을 표현하기에는 너무 ‘smooth’한 function만 estimate할 수 있다는 단점이 있다. 이를 해결하기 위해 이 논문에서는 Matern kernel function을 사용하며, 특히 그 hyperparameter로 5와 2를 사용하는 Matern 5/2를 사용하고 있다. 이 결과는 아무 값이나 고른건 아니고, 실제로 structured SVM의 hyperparameter를 찾을 때 여러 kernel function 중에서 가장 좋은 kernel이 무엇인지 아래와 같은 실험들 끝에 얻은 결과이다.

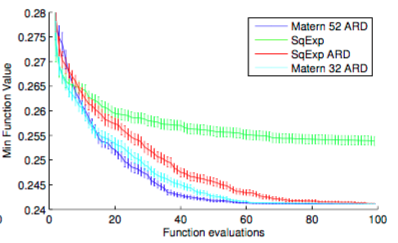
Matern 5/2 kernel의 구체적인 식은 다음과 같다.

따라서 이 GP의 hyperparameter는 $\theta_0, \theta_d$로, d가 1부터 D까지 있으니 총 D+1 개의 hyperparameter를 필요로 한다.

앞으로 별 다른 언급이 없다면 kernel function은 Matern 5/2, acquisition function으로는 EI를 사용한다.

Integrated Acquisition Function (marginalize hyperparameter)

이제 covariance의 형태를 결정했으니, GP의 hyperparameter를 없애는 일이 남았다. 우리가 optimize하고 싶은 hyperparameter의 dimension이 D라고 해보자 (위에서 언급했던 random forest의 경우, hyperparameter는 n_estimators, criterion, max_depth, min_samples_leaf로 D=4다). 이때 GP의 hyperparameter의 개수는 D+3개가 된다. 바로 앞에서 언급한 D+1개와, constant mean function의 값 m, 그리고 noise $\nu$가 그것이다.

이 논문에서는 hyperparameter를 완전하게 Bayesian으로 처리하기 위하여 모든 hyperparameter $\theta$ (D+3 dimensional vector)에 대해 acquisition function을 marginalize한 다음에, 다음과 같은 integrated acquisition function을 계산하는 방법을 제안한다.

PI와 EI에 대해서는 이 integrated acquisition function을 계산하기 위해 다양한 GP hyperparameter에 대한 GP posterior를 계산한 다음, integrated acquisition function의 Monte Carlo estimatation을 구하는 것이 가능하다. 이 논문에서는 slide sampling을 사용해 구할 수 있다고 언급되어있다. 말이 조금 어려운데, 그냥 쉽게 생각해보면, sampling을 통해 얻은 여러 hyperparameter들에 대해 EI를 전부 구한 다음, 그것들을 사용해 expectation 계산을 하면 integrated EI를 구할 수 있다. 그림으로 표현하면 아래와 같다.

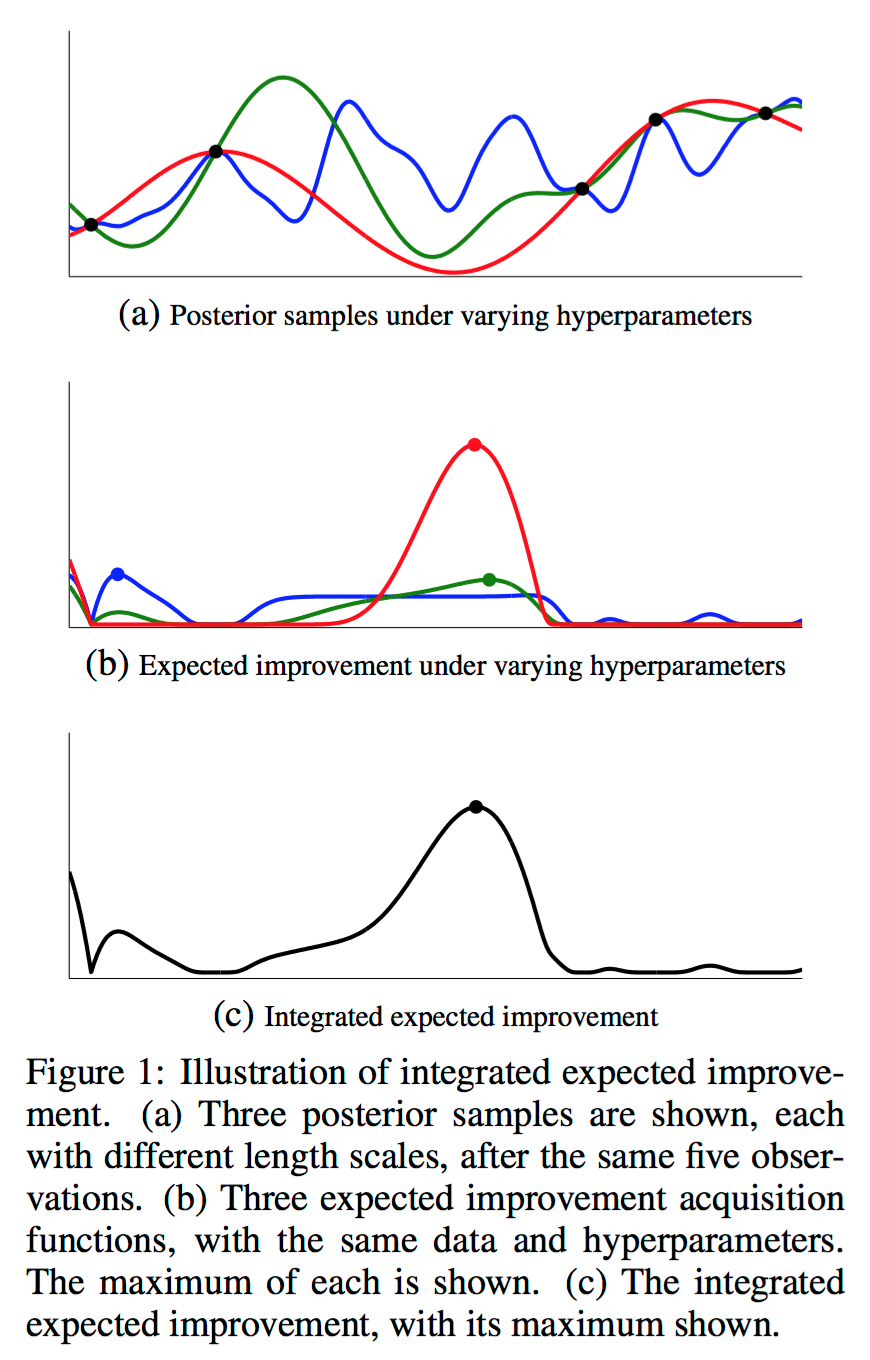
Expected Improvement per second

위에서 구한 integrated EI를 사용한다고 하더라도, 아직 몇 가지 문제점들이 남아있다. 그 중 하나는, 모든 hyperparameter에 대해 실험 시간이 똑같지 않다는 점이다. 예를 들어 deep learning layer가 2인 것과 500인 것은 실험 시간의 차이가 어마어마하다. 따라서 실제로는 가장 최소한의 시행을 통해 optimization을 진행한다고 하더라도, 실제 소요 시간은 엄청 클 수도 있는 것이다. 이 논문은 그런 문제를 해결하기 위해, 필요한 경우 EI per second 라는 새로운 acquisition function을 제안한다.

아마도 NIPS 논문이 page limitation이 빡빡해서 그런지 정확한 formulation은 나와있지 않지만, 요점은 objective function f(x) 말고도, duration function c(x) 라는 것을 따로 정의한 다음, 이 함수를 사용해 ‘cost’를 모델링하는 것이다. c(x)도 GP라고 assume하는 것 같은데, c(x)와 f(x)가 independent하다고 가정하면 쉽게 acquisition function을 구할 수 있는 모양이다. 아래 실험결과에서도 볼 수 있듯, 오히려 실제 실행 시간의 관점에서는 EI per second가 더 빠른 것을 알 수 있다.

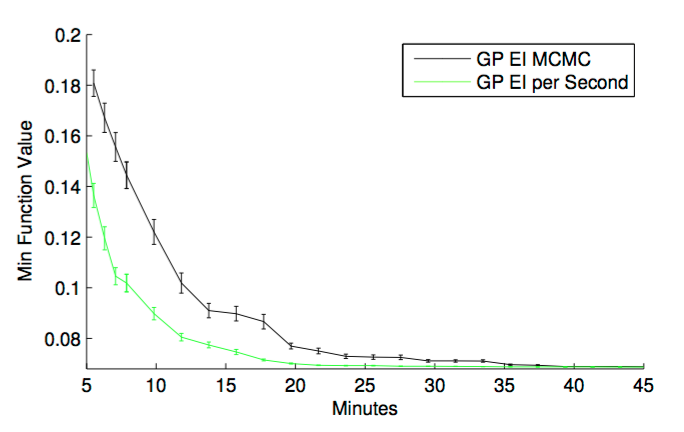
Monte Carlo Acquisition for Parallelizing Bayesian Optimization

이제 이 논문의 마지막 하이라이트만 남았다. Acquisition function을 optimize하면서 다음 point를 고르는 방식은 parallelization하기가 쉽지 않다. 매 번 포인트를 고를 때 마다 이 function이 바뀌기 때문인데, 여러 heuristic을 사용할 수는 있지만, theoretically tractable한 결과를 얻기는 쉽지 않다.

다음과 같은 문제 상황을 가정해보자. N개의 데이터의 evaluation이 끝난 상황이고 $(\{x_n, y_n\}_{n=1}^N)$ J개의 point들에서 $(\{x_j\}_{j=1}^J)$ 실험을 진행 중이라고 가정해보자. (아직 결과는 나오지 않았다) 이론상 지금까지 진행한 실험과 $(\{x_n, y_n\}_{n=1}^N)$ 현재 진행 중인 실험 $(\{x_j\}_{j=1}^J)$ 을 모두 고려하여 다음 point를 고르기 위해서는, acquisition function의 J개의 아직 결과가 나오지 않은 point들에 대한 expectation을 구한 다음, 그 결과를 acquisition function으로 사용하면 된다.

다행스럽게도, y가 Gaussian distribution이기 때문에 이 expectation은 쉽게 계산할 수 있으며, 단순히 동시에 진행하는 실험의 숫자를 늘리는 것으로 parallelization을 할 수 있기 때문에 parallelization 역시 간단하게 할 수 있다. 이 방법론을 GP EI MCMC라고 하며, 그림으로 나타내면 아래와 같다.

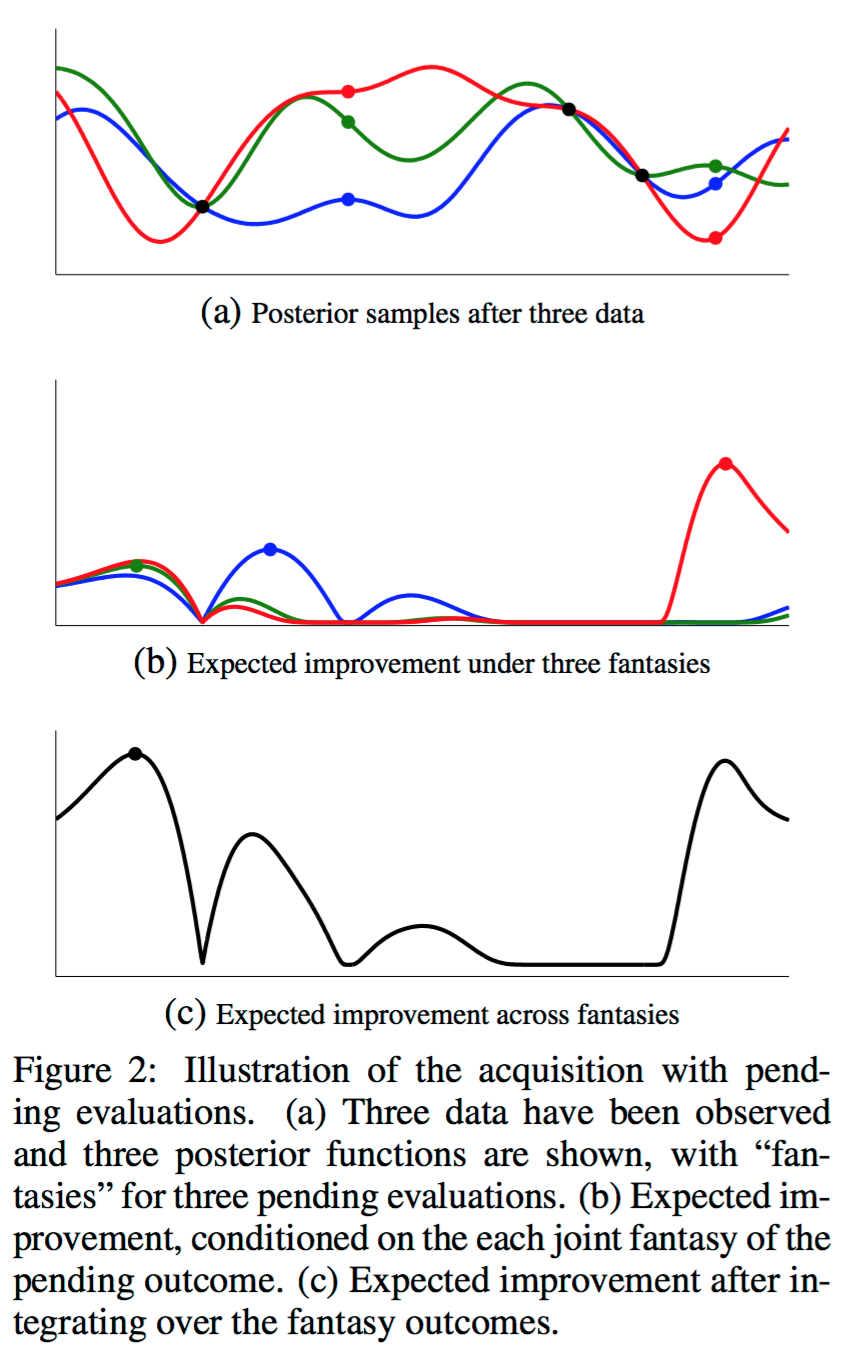
Conclusion

이 논문의 꽃이라 할 수 있는 실험 결과는 스킵하도록 하겠다. 그냥 “압도적으로 좋다” 정도로 이해하고 넘어가자. 사실 또 하나 언급하지 않은 점은, supplimentary material에 있는 구체적인 acquisition function optimization 방법이다. 이 논문은 개념적으로 알고 있어야하는 내용이 안그래도 많은데, 이 얘기를 하려면 여기에서 더 많은 얘기를 해야해서 넘기기로 하였다. 나중에 여유가 있을 때 추가 포스트를 쓰던가 해야겠다.

이 논문은 잘 쓰기만하면 굉장히 outperform한 성능을 낼 수 있는 Bayesian optimization 기반 hyperparameter search 알고리즘을 제안한다. 핵심은 어떻게 다음 point를 고를 것인지 설정하는 acquisition function을 design하느냐인데, 이 논문은 GP의 hyperparameter도 acquisition function에 녹이고, parallelization을 하기 위해 아직 진행 중인 실험의 expectation또한 이 acquisition function에 녹임으로써 원래 Bayesian optimization이 가지고 있었던 한계를 극복한다. 그뿐 아니라 실험적으로 우수한 kernel function인 Matern 5/2를 기본 kernel function제안함으로써 model selection 이슈도 피해간다.

실제 구현해서 사용하기는 어려운 내용이지만, 잘 숙지해두면 분명 도움이 될 수 있는 아이디어라 생각한다.

References

  1. [NIPS] Snoek, Jasper, Hugo Larochelle, and Ryan P. Adams. “Practical bayesian optimization of machine learning algorithms.”, 2012.
  2. [JMLR] Bergstra, James, and Yoshua Bengio. “Random search for hyper-parameter optimization.”, 2012
  3. http://becs.aalto.fi/en/research/bayes/courses/4613/Vik_Kamath_Presentation.pdf
  4. http://enginius.tistory.com/489
  5. Bayesian Optimization for Machine Learning, Ryan P.Adams, et. al
  6. [NIPS] Snoek, Jasper, Hugo Larochelle, and Ryan P. Adams. “Practical bayesian optimization of machine learning algorithms.” Supplimentary material, 2012.

변경 이력

  • 2016년 8월 16일: 글 등록