Distance Metric Learning

Machine Learning 분야에는 KNN 등의 input data의 distance metric을 어떻게 설정하냐 따라에 크게 영향을 받는 알고리듬들이 종종 존재한다. 그런데, 대부분 이런 method들에서 주로 사용하는 distance metric은 Euclidean distance로, 이 metric은 근본적으로 데이터 하나와 다른 데이터 하나와의 관계만을 나타내기 때문에 실제 distribution으로 존재하는 데이터에는 적합하지 않은 경우가 많다. 때문에 데이터들의 분포 등을 고려하여 이런 ‘거리’를 새로 정의하는 분야가 존재하는데 이를 일컬어 Distance Metric Learning이라 한다.

그렇다면 distance metric이란 무엇인가부터 간단하게 짚고 넘어가자. Distance metric은 쉽게 생각하면 distance를 정의하는 방법이라고 할 수 있다. 몇 가지 규칙이 존재하는데, 자세한 내용은 위키피디아 페이지를 참고하길 바란다. 역시 가장 간단한 예시는 Euclidean distance로, 우리가 가장 많이 알고 있는 거리를 측정하는 방법일 것이다. 이 함수는 간단하게 $d(p,q)=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2+…}$로 정의된다. 그 밖에도 두 점의 값이 정확히 일치하면 1, 일치하지 않는다면 0으로 표시하는 binary distance등도 존재한다.

이 밖에도 중요한 distance metric으로는 Mahalanobis Distance Metric이라는 것이 있다. 이 distance metric은 Euclidean distance metric이 data set의 correlation을 하나도 고려하지 않은 문제점을 해결할 수 있고, 또한 scale-invariant한 특성을 가지고 있다. 이 metric은 $d(p,q)=\sqrt{(\vec p - \vec q)^\top \Omega (\vec p - \vec q)}$로 정의된다. 이 때 $\Omega$는 semidefinite matrix이다. 위키피디아에서 발췌한 보다 정확한 정의는 앞서 나왔던 수식에서 $\Omega$가 covariance matrix인 metric이다. 따라서 이 metric이 data set의 correlation을 포함하여 거리를 표현할 수 있는 것이다. 하지만 실제 분포를 알 수 없는 임의의 데이터들에 대해서 올바른 covariance matrix를 계산하는 것은 매우 어렵다. 따라서 이 Mahalanobis metric의 $\Omega$를 learning하는 method들도 존재하는데, 대표적으로 LMNN(Large Margin Nearest Neighbor) classification이 있다. 이 논문에 대해서는 추후에 따로 포스트를 하도록 하겠다.

아무튼, distance metric learning은 input data space에서 data들에 가장 적합한 형태의 어떤 metric을 learning하는 알고리듬이다. 여기에서 data는 각 pair 별로 similar/dissimilar가 정의되어 있는 형태의 데이터이다. 즉, metric learning은 similar한 point끼리는 더 가까운 거리로 판단하게 하고, dissimilar한 point는 더 먼 거리로 판단하게 하는 어떤 metric을 학습하는 것이다. 당연히 KNN 등의 알고리듬들은 그 성능이 크게 개선될 수 있다.

아래는 distance metric learning을 간략하게 그림으로 나타낸 것이다. 그림은 Bellet, A., Habrard, A., and Sebban, M. A Survey on Metric Learning for Feature Vectors and Structured Data, 2013 에서 발췌하였다.

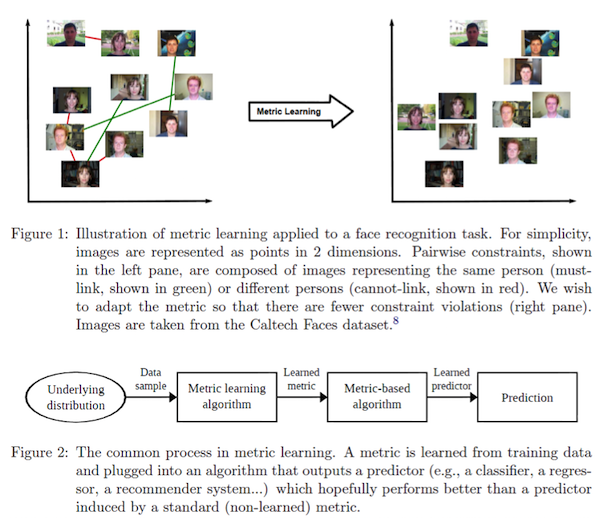
즉, 우리가 metric learning을 하는 가장 큰 이유는 KNN 등의 metric에 크게 좌우되는 algorithm들의 성능을 개선시키기 위함인 것이다.

그렇다면 distance metric learning의 종류는 어떻게 되는가? 일반적인 machine learning 분류처럼 supervised/unsupervised learning이 존재한다. 먼저 supervised learning은 constraints나 label이 이미 주어진 상태에서 metric을 학습하게 된다. 즉, 이미 우리는 모든 데이터들의 관계를 알 고 있고, 이 관계에서 가장 적합한 distance metric을 찾는 알고리듬인 것이다. 대표적으로 NCA, RCA 등의 알고리듬 들이 존재한다고 한다. 이에 반해 unsupervised learning은 아무런 사전지식없이 metric을 learning하는데, 주로 dimension reduction technique으로 많이 사용한다. 예를 들어서 PCA가 이 범주에 들어가게 된다.

내가 읽은 두 개의 survery에서는 (Liu Yang, Distance Metric Learning: A Comprehensive Survey, 2005 그리고 Liu Yang, An Overview of Distance Metric Learning, 2007) 이 두 가지 분류 뿐 아니라 두 가지 분류를 더 추가하였다. 하나는 Maximum margin based distance learning이고, 또 하나는 kernel method이다. 일단 kernel 쪽은 내가 잘 모르기도 하고, 내 관심사는 maximum margin based distance learning이므로, 이 부분에 조금 더 집중해서 설명하도록 하겠다.

위의 survey에서 정의하는 Maximum margin based learning은 다음과 같다. “Formulate distance metric learning as a constrained convex programming problem, and attempt to learn complete distance metric from training data” 즉, Convex optimization을 통해서 가장 최적의 metric을 찾아내는 method라는 것이다. 여기에서 convex optimization은 이전에 블로그에서 다룬 적이 없기 때문에 나중에 이에 대한 글을 쓰게 되면 여기에 추가 랑크를 달도록 하고 지금은 일단 위키피디아 링크로 설명을 대체하도록 하겠다. 링크

이 방법은 주어진 input에 대해서 가장 최고의 performance를 내는 metric을 찾아내기 때문에 가장 성능이 좋아보일 것 같지만, 실제로는 몇 가지 문제점들을 가지고 있다. 하나, convex optimization은 대부분 gradient descent method를 사용하여 그 계산하는데, 이 계산량이 다른 method들에 비해서 많이 비싸다. 둘째, input training data들에 대해서 optimize한 결과로 metric을 정의하기 때문에 overfitting 문제가 발생할 수 있다. 특히 이 overfitting은 dimesion이 높아질 수록, traing sample의 숫자가 줄어들 수록 더더욱 문제가 된다. 때문에 이런 문제점을 해결하기 위해서 dimension을 reduction한 이후에 metric을 learning하는 등의 technique들이 사용되고 있다. 하지만 이 역시 문제가 있는데, 이 문제에 대해서는 나중에 포스팅하게 될 LMCA 논문에서 다루도록 하겠다.

아무튼 maximum margin based learning의 대표적인 예는 LMNN method로, 이 method는 위에서 설명했던 Mahalanobis metric을 직접 learning하며, non-convex problem을 Semidefinite problem으로 바꾸어 global optimum을 찾는 문제로 바꾸어서 계산을 하게 된다. 이 논문에 대해서는 나중에 다시 포스팅하도록 하겠다.

혹시 이 부분에 대해서 더 자세히 알고 싶다면, 아래에 링크해놓은 tutorial들을 읽어보길 바란다.

Tutorials

References

Liu Yang, Distance Metric Learning: A Comprehensive Survey, 2005
Liu Yang, An Overview of Distance Metric Learning, 2007
Bellet, A., Habrard, A., and Sebban, M. A Survey on Metric Learning for Feature Vectors and Structured Data, 2013
K.Q.Weinberger,J.Blitzer,andL.K.Saul(2006).InY.Weiss,B.Schoelkopf, and J. Platt (eds.), Distance Metric Learning for Large Margin Nearest Neighbor Classification, Advances in Neural Information Processing Systems 18 (NIPS-18). MIT Press: Cambridge, MA.