Batch Normalization은 현재 ImageNet competition에서 state-of-art (Top-5 error: 4.9%)를 기록하고 있는 Neural Network model의 기본 아이디어이다. 이 글에서는 arXiv에 제출된 (그리고 ICML 2015에 publish된) Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 논문을 리뷰하고, batch normalization이 어떤 기술이고, 어떤 원리에 의해 작동하는지 등에 대해 다룰 것이다.

Motivation: Deep learning의 속도를 어떻게 더 빠르게 만들 수 있을까?

Deep learning이 잘 동작하고, 뛰어난 성능을 보인다는 것은 이제 누구나 알고 있다. 그러나 여전히 deep learning은 굉장히 시간이 오래 걸리는 작업이고, 그만큼 computation power도 많이 필요로 한다. 그 동안의 연구 결과를 보면, converge한 것 처럼 보이더라도 더 많이 돌리게 된다면 더 좋은 결과로 수렴한다는 것을 알 수 있는 만큼, deep neural network의 train 속도를 높이는 것은 전체적인 성능 향상에 도움이 될 것이다.

보통 Deep learning을 train할 때에는 stochastic gradient descent (SGD) method를 사용한다. SGD의 속도를 높이는 가장 naive한 방법은 learning rate를 높이는 것이지만, 높은 learning rate는 보통 gradient vanishing 혹은 gradient exploding problem을 야기한다는 문제가 있다.

Gradient vanishing은 backpropagation algorithm에서 아래 layer로 내려갈수록, 현재 parameter의 gradient를 계산했을 때 앞에서 받은 미분 값들이 곱해지면서 그 값이 거의 없어지는 (vanish하는) 현상을 의미한다. Gradient exploding은 learning rate가 너무 높아 diverge하는 현상을 말한다. Learning rate의 값이 크면 이 두 가지 현상이 발생할 확률이 높기 때문에 우리는 보통 작은 learning rate를 고르게 된다. 그러나 우리는 이미 일반적으로 learning rate의 값이 diverge하지 않을 정도로 크면 gradient method의 converge 속도가 향상된다는 것을 알고 있다. 따라서 이 논문이 던지는 질문은 다음과 같다. 자연스럽게 나오는 궁금증은 Gradient vanishing/exploding problem이 발생하지 않도록 하면서 learning rate 값을 크게 설정할 수 있는 neural network model을 design할 수 있는가?

Internal Covariate Shift: learning rate의 값이 작아지는 이유

Gradient vanishing problem이 발생하는 이유에 대해서는 여러가지 설명이 가능하지만 (exploding은 그냥 우리가 값을 작게 설정하여 해결할 수 있다) 이 논문에서는 internal covariate shift라는 개념을 제안한다. Covariate shift는 machine learning problem에서 아래 그림과 같이 train data와 test data의 data distribution이 다른 현상을 의미한다. 아래 그림 참고 (출처)

이 논문에서는 단순히 train/test input data의 distribution이 변하는 것 뿐 아니라, 각각의 layer들의 input distribution이 training 과정에서 일정하지 않기 때문에 문제가 발생한다고 주장하며, 이렇게 각각의 layer들의 input distribution이 consistent하지 않은 현상을 internal convariate shift라고 정의한다. 이 논문에서 이것이 문제가 된다고 주장하는 이유는, 각각의 layer parameter들은 현재 layer에 들어오는 input data 뿐만 아니라 다른 model parameter들에도 영향을 받기 때문이라고한다. 즉, gradient vanishing problem이 발생하는 이유를 backpropagation 과정에서 아래로 내려갈수록 이전 gradient들의 영향이 더 커져서 지금 parameter가 거의 update되지 않는다고 설명하는 것과 같은 맥락이다.

기존에는 이런 현상을 방지하기 위하여 ReLU neuron을 사용하거나 (Nair & Hinton, 2010), cafeful initialization을 사용하거나 (Bengio & Glorot, 2010; Saxe et al., 2013), leanring rate를 작게 취하는 등의 전략을 사용했지만, 그런 방법이 아닌 다른 방법을 통해 internal covariate shift 문제가 해결이 된다면 더 높은 learning rate를 선택하여 learning 속도를 빠르게하는 것이 가능할 것이다.

Navie approach: Whitening

따라서 이 논문의 목표는 internal covariate shift를 줄이는 것이다. 그렇다면 internal covariate shift는 어떻게 줄일 수 있을까? 이 논문에서는 엄청 간단하게 input distribution을 zero mean, unit variance를 가지는 normal distribution으로 normalize 시키는 것으로 문제를 해결하며, 이를 whitening이라한다 (LeCun 1998, Wiesler & Ney 2011). 주어진 column data $X\in R^{d\times n}$에 대해 whitening transform은 다음과 같다.

$$\hat{X} = Cov(X)^{-1/2} X, Cov(X) = E[( X - E[X] ) ( X - E[X] )^\top ].$$

그러나 이런 naive한 approach에서는 크게 두 가지 문제점들이 발생하게 된다.

1. multi variate normal distribution으로 normalize를 하려면 inverse의 square root를 계산해야 하기 때문에 필요한 계산량이 많다.
2. mean과 variance 세팅은 어떻게 할 것인가? 전체 데이터를 기준으로 mean/variance를 training마다 계산하면 계산량이 많이 필요하다.

따라서 이 논문에서는 이런 문제점들을 해결할 수 있으면서, 동시에 everywhere differentiable하여 backpropagation algorithm을 적용하는 데에 큰 문제가 없는 간단한 simplification을 제안한다.

Batch Noramlization Transform

앞서 제시된 문제점들을 해결하기 위하여 이 논문에서는 두 가지 approach를 제안한다.

1. 각 차원들이 서로 independent하다고 가정하고 각 차원 별로 따로 estimate를 하고 그 대신 표현형을 더 풍성하게 해 줄 linear transform도 함께 learning한다
2. 전체 데이터에 대해 mean/variance를 계산하는 대신 지금 계산하고 있는 batch에 대해서만 mean/variance를 구한 다음 inference를 할 때에만 real mean/variance를 계산한다

먼저 naive approach에서 covariance matrix의 inverse square root를 계산해야했던 이유는 모든 feature들이 서로 correlated되었다고 가정했기 때문이지만, 각각이 independent하다고 가정함으로써, 단순 scalar 계산만으로 normalization이 가능해진다. 이를 수식으로 표현하면 다음과 같다.

d dimensional data $x = (x^{(1)}, x^{(2)}, \ldots, x^{(d)})$에 대해 각각의 차원 $k$ 마다 다음과 같은 식을 계산하여 $\hat x$를 계산한다

$$\hat{x}^{(k)} = \frac{x^{(k)} - E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}.$$

그러나 이렇게 correlation을 무시하고 learning하는 경우 각각의 관계가 중요한 경우 제대로 되지 못한 training을 하게 될 수도 있으므로 이를 방지하기 위한 linear transform을 각각의 dimension $k$마다 learning해준다. 이 transform은 scaling과 shifting을 포함한다.

$$y^{(k)} = \gamma \hat{x}^{(k)} + \beta.$$

이때 parameter $\gamma, \beta$는 neural network를 train하면서 마치 weight를 update하듯 같이 update하는 model parameter이다.

두 번째로, 전체 데이터의 expectation을 계산하는 대신 주어진 mini-batch의 sample mean/variance를 계산하여 대입한다.

이제 앞서 설명한 두 가지 simplification을 적용하여 다음과 같은 batch normalization transform이라는 것을 정의할 수 있다.

이때, backpropagation에 사용되는 $\gamma, \beta$ 그리고 layer를 위한 chain rule은 다음과 같이 계산된다.

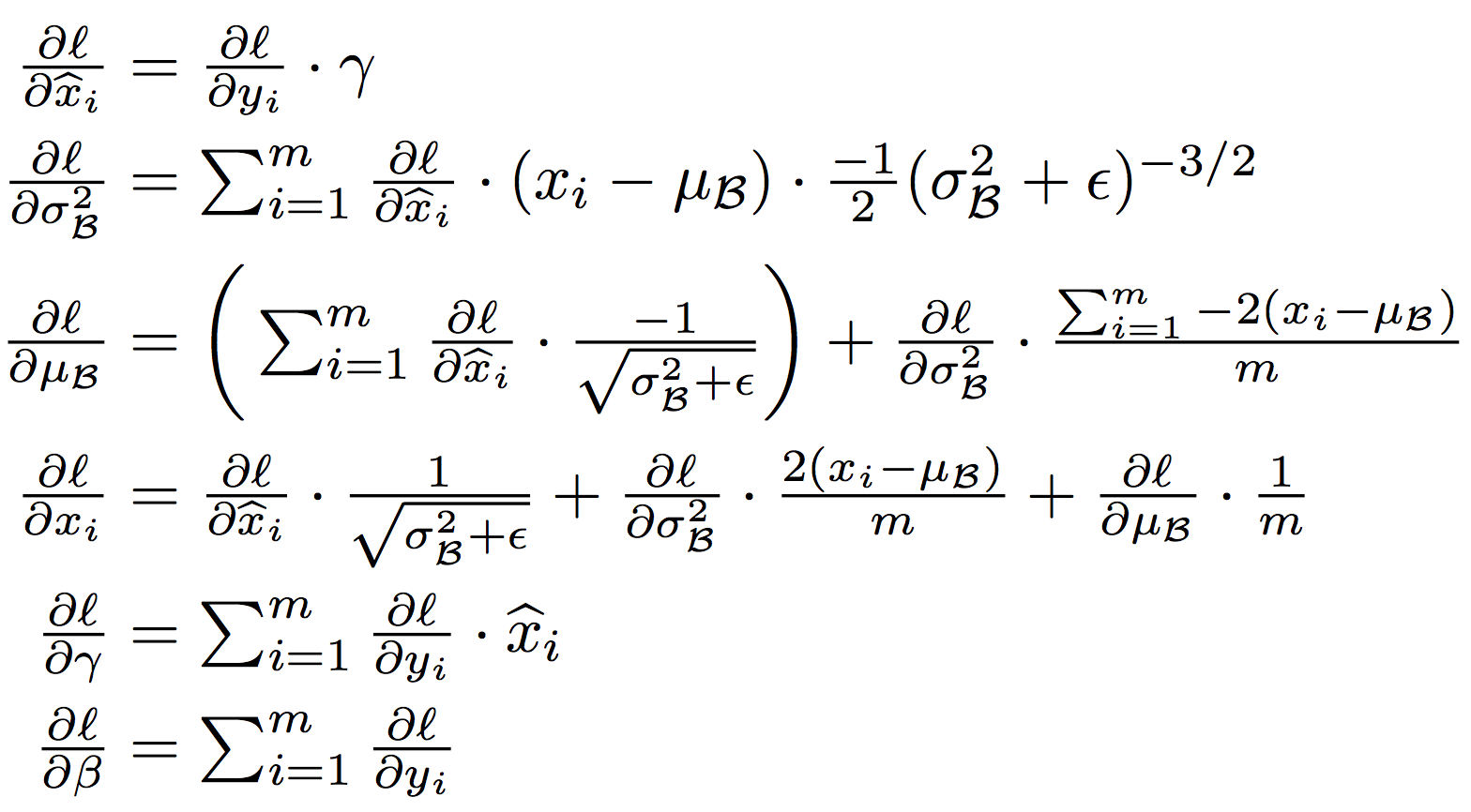
Train/Inference with BN network

앞에서 batch normalization transform을 각각의 layer input을 normalization하는데에 사용할 것이라는 설명을 했었다. 다시말해서 BN network는 기존 network에서 각각의 layer input 앞에 batch normalization layer라는 layer를 추가한 것과 구조가 동일하다.

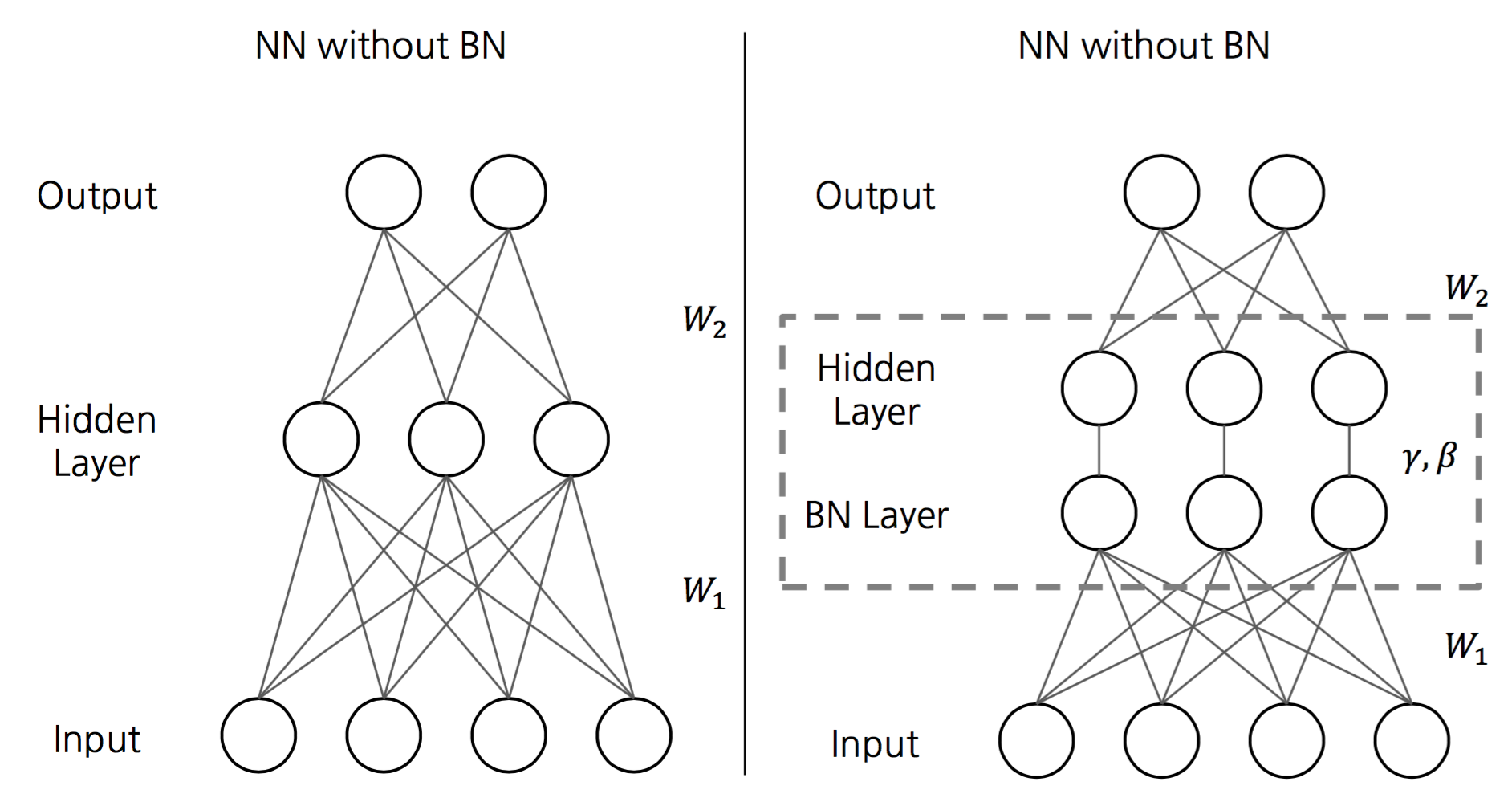
이때 자세한 알고리즘은 다음과 같다.

주의해야할 점 하나는 train 과정에서는 mini-batch의 sample mean/variance를 사용하여 BN transform을 계산하였지만, inference를 할 때에도 같은 규칙을 적용하게 되면 mini-batch 세팅에 따라 inference가 변할 수도 있기 때문에 각각의 test example마다 deterministic한 결과를 얻기 위하여 sample mean/variance 대신 그 동안 저장해둔 sample mean/variance들을 사용하여 unbiased mean/variance estimator를 계산하여 이를 BN transform에 이용한다.

BN network의 장점

저자들이 주장하는 BN network의 장점은 크게 두 가지이다.

1. 더 큰 learning rate를 쓸 수 있다. internal covariate shift를 감소시키고, parameter scaling에도 영향을 받지 않고, 더 큰 weight가 더 작은 gradient를 유도하기 때문에 parameter growth가 안정화되는 효과가 있다.
2. Training 과정에서 mini-batch를 어떻게 설정하느냐에 따라 같은 sample에 대해 다른 결과가 나온다. 따라서 더 general한 model을 learning하는 효과가 있고, drop out, l2 regularization 등에 대한 의존도가 떨어진다.

논문을 살펴보면 BN transform이 scale invariant하고, 큰 weight에 대해 작은 gradient가 유도되기 때문에 paramter growth를 안정화시키는 효과가 있다는 언급이 있다. 또한 regularization효과를 더 강화하기 위하여 매 mini-batch마다 training data를 shuffling하여 input으로 넣는데, 이때 한 mini-batch 안에서는 같은 데이터가 중복으로 나오지 않도록 shuffling하여 대입한다.

실험

먼저 BN network가 주장하는대로 잘 동작하는지 보여주는 실험이다.

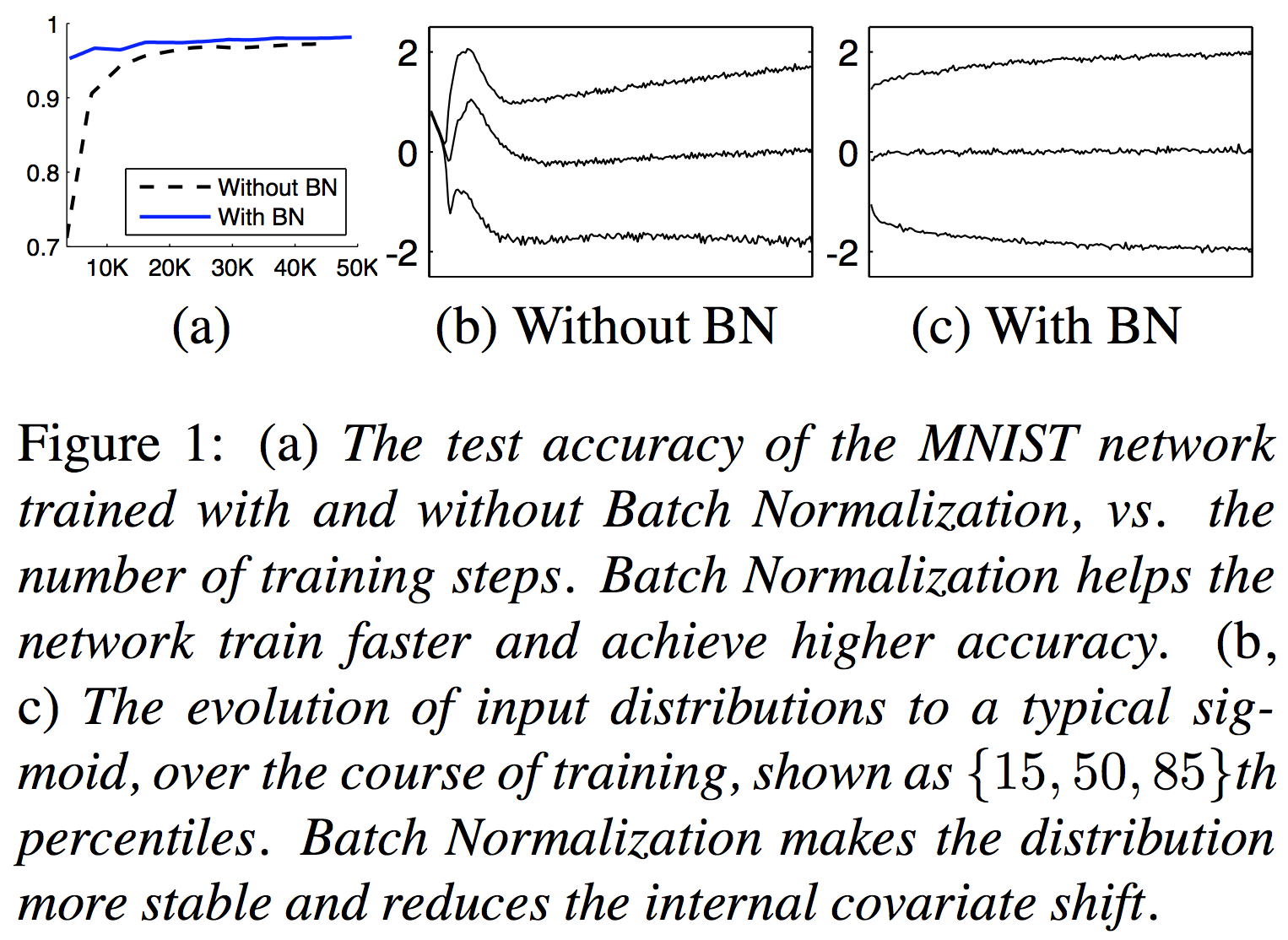
가장 왼쪽은 MNIST data에 대해 BN을 쓴 것과 쓰지 않은 것의 convergence speed를 비교한 것이며, 다음 그림들은 BN을 사용했을 때와 사용하지 않았을 때, internal covariate shift가 어떻게 변화하는지를 보여주는 것이다. 한 뉴런의 training 동안 activation value의 변화를 plot한 것으로, 가운데 있는 선이 평균 값이고, 위 아래가 variance를 의미한다고 생각하면 된다. BN을 사용하면 처음부터 끝까지 거의 비슷한 distribution을 가진다는 것을 알 수 있다.

다음으로 single network에 대해 inception network와의 성능을 비교한 실험이다

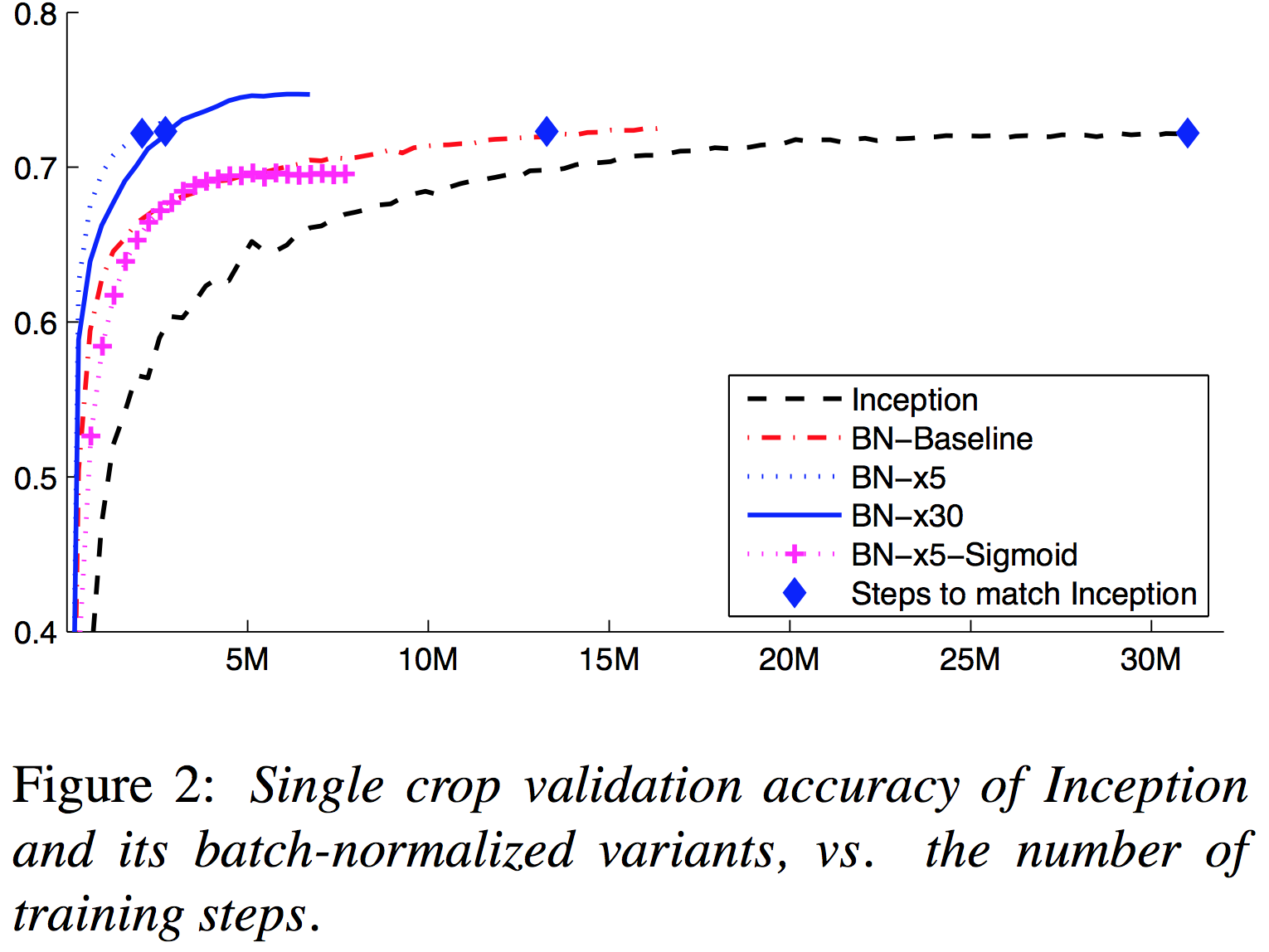
세팅은 전부 같고 inception network와 비교하여 BN이 추가되었는지 여부와 learning rate가 몇 배인지 (x5는 5배의 leanring rate를 취한 것이다) 여부만 다르게 설정하였음에도 불구하고 convergence speed와 심지어 최종 max acc까지 차이가 나는 것을 볼 수 있다.

이런 결과들을 기반으로 약간의 paramter tunning을 거쳐 아래와 같은 ImageNet state-of-art를 기록했다고 한다.

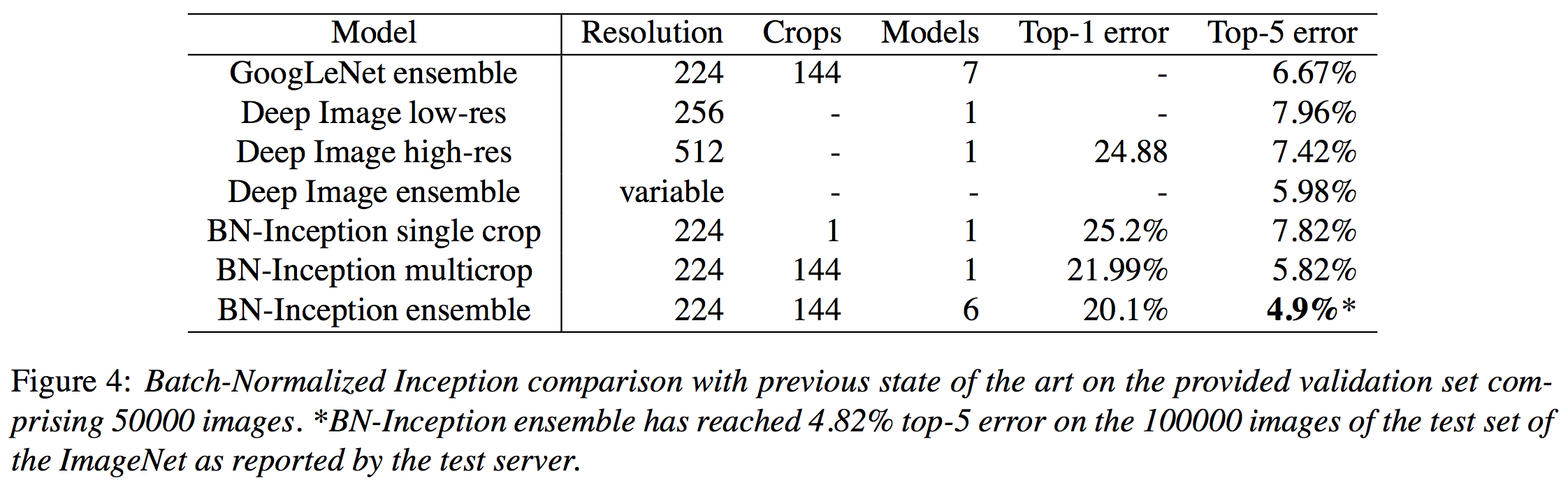
BN 네트워크 성능 accelerating하기

BN을 추가하는 것 만으로 성능 개선이 엄청나게 일어나는 것은 아니며 다음과 같은 parameter tunning이 추가로 필요하다고 한다. 1. learning rate 값을 키운다 (0.0075 -> 0.045, 5) 2. drop out을 제거한다 (BN이 regularization 효과가 있기 때문이라고 한다) 3. l2 weight regularization을 줄인다 (BN이 regularization 효과가 있기 때문이라고 한다) 4. learning rate decay를 accelerate한다 (6배 더 빠르게 가속한다) 5. local response normalization을 제거한다 (BN에는 적합하지 않다고 한다) 6. training example의 per-batch shuffling을 추가한다 (BN이 regularization 효과를 증폭시키기 위함이다) 7. photometric distortion을 줄인다 (BN이 속도가 더 빠르고 더 적은 train example을 보게 되기 때문에 실제 데이터에 더 집중한다고 한다)

이런 parameter tunning이 추가로 이루어지고 나면, 기존 neural network보다 ImageNet에서 훨씬 좋은 성능을 내는 neural network를 구성할 수 있다고 한다.

Summary of BN network

• 아이디어: 각 nonlinearity의 input으로 BN transform을 추가한다
• BN transform은 다음과 같은 두 가지 simplification으로 구성된다
  • 각 feature들의 correlation을 무시하고 각각 따로 normalize 하고 각각에 대한 linear transform을 같이 learning한다
  • Mini-batch의 sample mean/variance로 normalize 한다
• BN network의 train/inference에서는 다음과 같은 특이점이 있다
  • Train/inference의 forward rule이 다르다 (각각이 사용하는 mean/variance가 다르다)
  • Train 과정에서 mini-batch를 (중복없이) shuffling하여 train시킨다
• BN network를 사용함으로써 다음과 같은 효과를 볼 수 있다
  • Learning rate를 큰 값으로 설정할 수 있어 converge가 빠르다
  • Generalized model을 learning하는 효과가 있다

Reference

• Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, Sergey Ioffe, Christian Szegedy, ICML 2015