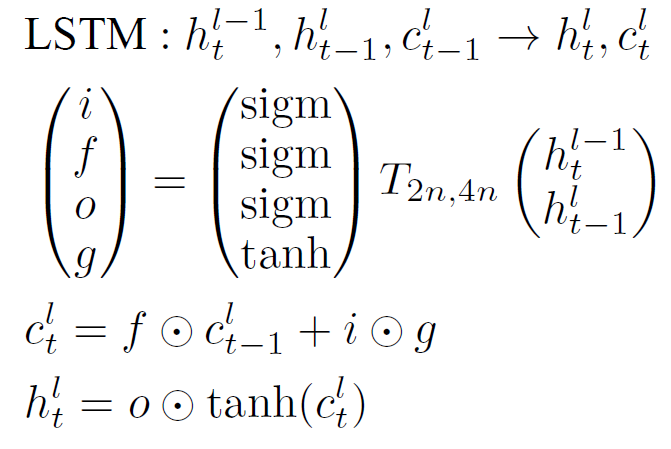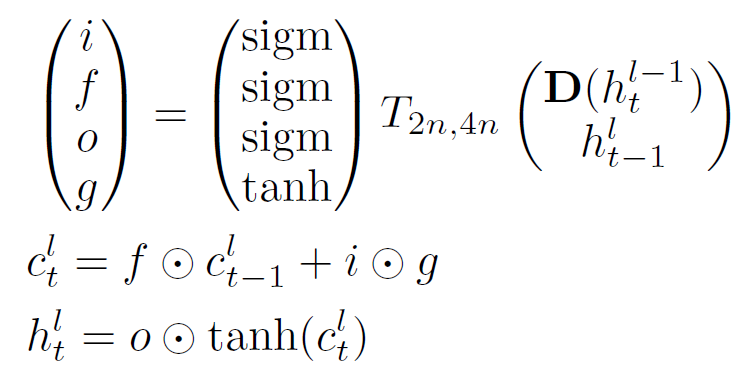이번에 review할 논문은 Recurrent neural network regularization이라는 논문이다. 아직 학회나 저널에 publish된 논문은 아니지만 ICLR 2015 review를 기다리는 모양. 이 논문은 최근 머신러닝 분야에서 가장 주목받고 있는 분야는 Deep learning, 그 중에서도 요즘 가장 활발하게 연구 중인 Recurrent Neural Network, 혹은 RNN에 관한 논문이다. RNN은 sequencial data를 처리하는데에 적합한 형태로 디자인 되어있으며, 현재 language model, speech recognition, machine translation 등에서 우수한 결과를 성취하고 있는 neural network model 중 하나이다. 이 논문은 popular한 RNN 중 하나인 LSTM 모델을 regularization 시켜서 보다 기존 결과들보다 더 잘 동작하는 결과를 제안한다.
Motivation: Regularization of Recurrent Neural Network
RNN이 sequencial data에 대해 꽤 좋은 성능을 보이고 있는 것은 사실이지만, RNN을 regularization하는 방법은 많이 제안되어있지 않은 상황이다. 기존 MLP (Multi-Layer Perceptron, 혹은 feed-forward network) 쪽에서는 Dropout, ReLU 등의 컨셉들이 연구되면서 상당한 발전이 있었지만, 아직 RNN에는 Dropout조차 제대로 적용되지 않고 있다고 한다. Dropout을 붙이면 오히려 성능이 떨어지기 때문에 아직은 LSTM (Long-Short-Term-Memory) 모델에 dropout없이 연구가 진행되고 있는 모양이다. 이 논문에서는 LSTM에 dropout을 RNN의 특성을 잘 살린 형태로 적용하여 dropout이 잘 동작하도록 하는 방법을 제안한다.
RNN Introduction
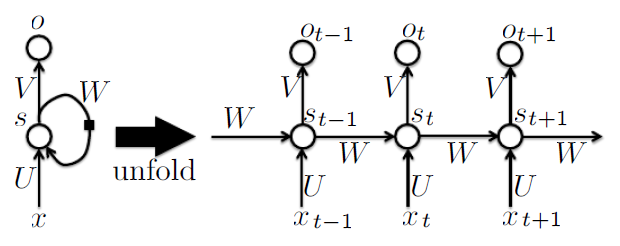
본 논문을 소개하기 전에 먼저 RNN에 대해 간단하게 설명을 하고 넘어가도록 하겠다. 이름에서도 알 수 있듯 일반적인 Feed-forward network와 RNN의 차이는 recurrent한 loop의 존재 유무이다. 이는 자기 자신을 향한 self-loop일 수도 있고, 아니면 cycle 형태이거나 아니면 undirected edge의 형태일 수도 있다. 보통 일반적으로 RNN이라 하면 아래 그림과 같이 hidden unit에 self-loop이 있는 형태를 일컫는 듯하다. (출처: Bengio Deep Learning book)
이 그림에서도 알 수 있듯 self-loop의 존재는 RNN으로 하여금 자연스럽게 historical data를 현재 decision에 반영하도록 만들어준다. 즉, RNN 모델은 마치 HMM 등의 sequencial data를 처리하는 모델들처럼 동작하는 것이다. 실제 learning을 할 때는 시간에 대해 self-loop를 ‘unfold’ 하여 마치 weight를 공유하는 deep layer를 연산하듯 update한다. RNN에 대한 더 자세한 설명은 추후 다른 포스팅을 통해 다룰 수 있도록 하겠다.
Long-Short-Term-Memory (LSTM) Architecture
기존 vanilla RNN은 long-term dependency를 가지도록 learnig을 하게되면 gradient vanishing이나 exploding 문제에 직면하기 쉬워진다. 이유는 dependency를 더 long-term으로 가져갈수록 gradient 값이 시간에 따른 곱하기 형태가 되어 gradient growth가 exponential해지기 때문이다 (역시 위와 마찬가지로 나중에 더 자세하게 다루도록 하겠다). 때문에 이를 해결하기 위한 아이디어 중 하나로 LSTM이라는 것이 존재한다.
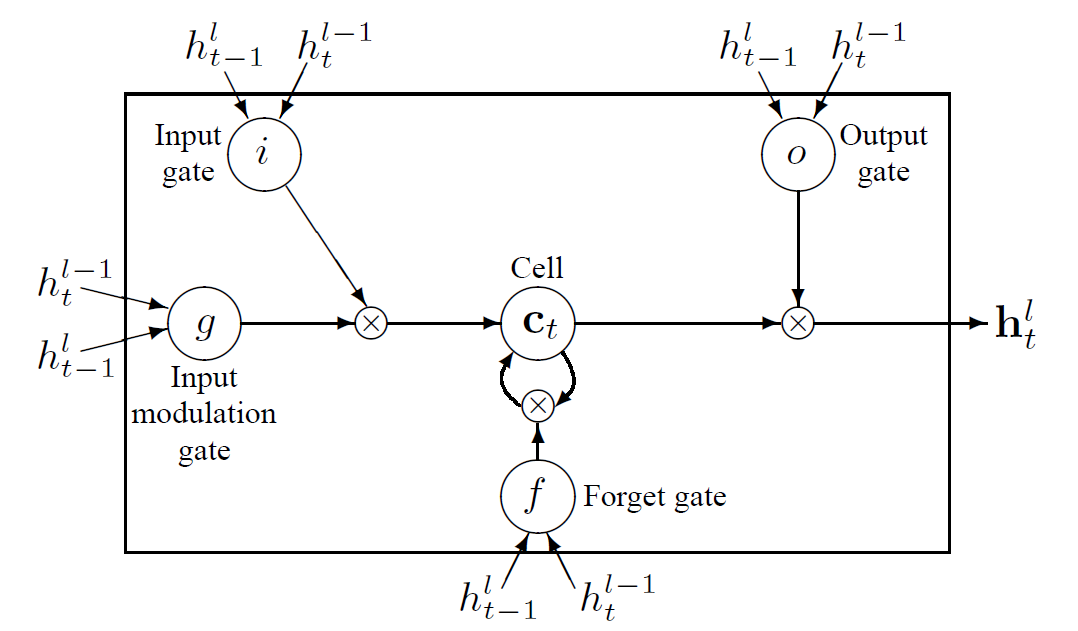
LSTM은 historical information을 저장하기 위한 다소 복잡한 dynamics를 가지고 있다. “long term” memory라는 것은 memory cell ($c_t$)에 저장되며, 시간에 따라, 그리고 주어진 input data에 따라 저장해둔 information을 얼마나 간직하고 있을지 forget gate ($f_t$) 라는 것을 통해 결정하게 된다. LSTM을 그림으로 표현하면 아래 그림과 같다. (출처: 논문)
이를 수식으로 한 번 나타내어보자. 먼저 몇 가지 notation을 정의해보자. 먼저 모든 state는 n-dimension이라고 가정하자. $h_t^l \in \mathbb R^n $은 layer $l$의 timestamp $t$일 때의 hidden state라고 하자. 그리고 $T_{n,m}: \mathbb R^n \to \mathbb R^m$ 을 n차원에서 m차원으로 가는 affine transform이라고 해보자. 예를 들어 parameter $W$와 $b$로 나타내어지는 $Wx + b$도 $T_{n,m}$에 포함된다 (즉, 이 논문에서는 복잡한 weight와 bias에 대한 식을 T라는 notation으로 간단하게 치환했다고 생각하면 된다). 마지막으로 $\odot$을 두 벡터의 element-wise multiplication이라고 정의해보자. 이렇게 notation을 정의하고 나면 일반적인 vanilla RNN을 다음과 같이 과거의 hidden state와 현재 hidden state의 이전 layer의 state로부터 현재 hidden state를 표현하는 function으로 표현할 수 있다.
$$\mbox{RNN: } h_t^{l-1}, h_{t-1}^l \to h_t^l, \mbox{ where } h_t^l = f(T_{n,n} h_t^{l-1} + T_{n,n} h_{t-1}^l). $$
이때, function $f$는 RNN의 경우 sigmoid나 tanh 함수 중 하나로 선택하는 것이 일반적이다. 그럼 이번에는 LSTM을 수식으로 표현해보자.
앞에서 언급했던 LSTM의 graphical representation을 살펴보면서 수식을 읽어보면 어렵지 않게 이해할 수 있을 것이다.
Dropout Regularization for LSTM
저자들은 RNN에 Dropout을 붙였을 때 잘 동작하지 않는 이유가 dropout이 지워버리면 안되는 과거 information까지 전부 지워버리기 때문이라고 주장한다. 때문에 RNN에 Dropout을 적용하기 위해서는 recurrent connection이 아닌 connection 들에 대해서만 Dropout을 적용해야한다고 논문에서는 주장하고 있다. 아래 식에 조금 더 자세하게 적혀있다. 이때 $\mathbf D$ 는 dropout operator라는 것으로, 주어진 argument의 random subset을 0으로 만들어버리는 operator이다. 즉, $\mathbf D (h)$ 라고 한다면 vector $h$ 중 random하게 고른 일부를 (보통 50%) 0으로 설정하라는 뜻이다.
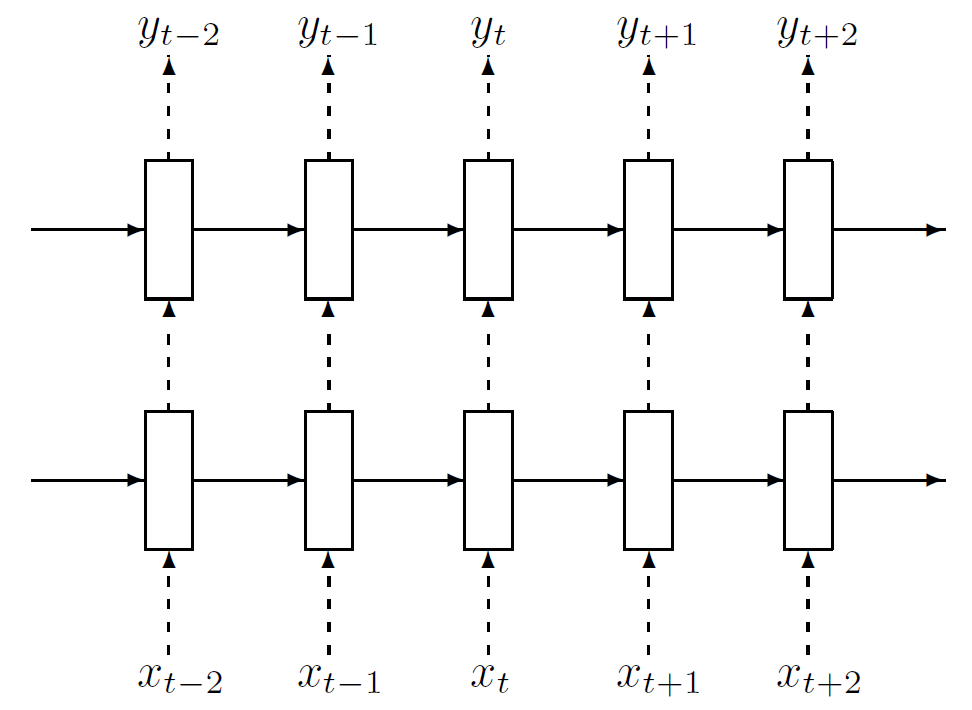
이를 그림으로 표현하면 아래와 같다. 이때 실선은 일반적인 connection이고, 점선이 dropout으로 연결된 connection을 의미한다. (출처: 논문)
위 그림에서도 알 수 있듯, 과거에서부터 propagation되는 information은 언제나 100% 보존되지만, 아래 layer에서 위 layer로 전달되는 information은 특정 확률로 dropout에 의해 corruption되어 진행된다. 이때, 맨 아래 data layer로부터 맨 위 $L$번째 layer까지 information이 전달되는 동안 점선으로 그려진 connection은 정확하게 $L+1$ 번 만큼만 지나게 된다. 만약 recurrent connection까지 dropout을 적용했다면, 이 횟수는 $L+1$ 보다 항상 같거나 클 것이며, 더 long-term dependency를 가질수록 그 효과가 더 강해져서 우리가 원하는 과거 정보는 거의 다 희석되고, 결과적으로 안좋은 결과를 얻게 될 확률이 높아질 것이다.
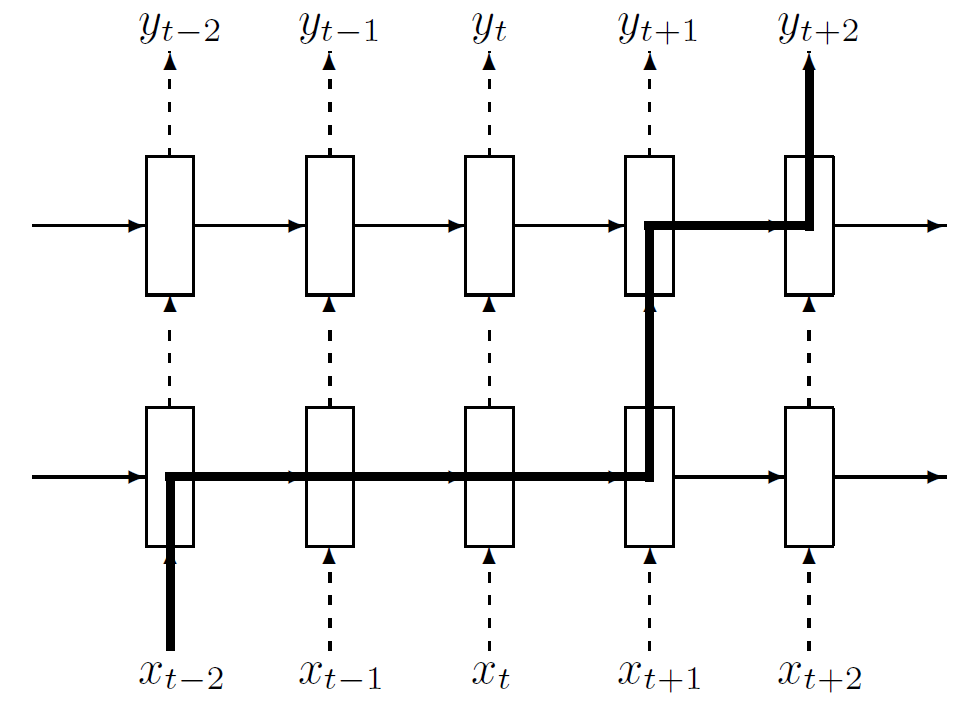
위 그림은 어떻게 information이 time t-2로부터 t+2까지 전달되는지 그 flow를 표현한 것이다. 굵은 선이 information path를 나타내는데, 앞서 설명한 것 처럼 이런 information flow는 data layer로부터 decision layer까지 정확하게 $L+1$ 번만 dropout의 영향을 받게 된다. 반면 standard dropout을 적용했더라면 information이 더 많은 dropout들에 의해 영향을 받아서 LSTM이 정보를 더 긴 시간 동안 저장할 수 없도록 만들게 되는 것이다. 때문에 recurrent connection에 dropout을 적용하지 않는 것 만으로도 LSTM에서 좋은 regularization 효과를 얻을 수 있는 것이다.
Experiments
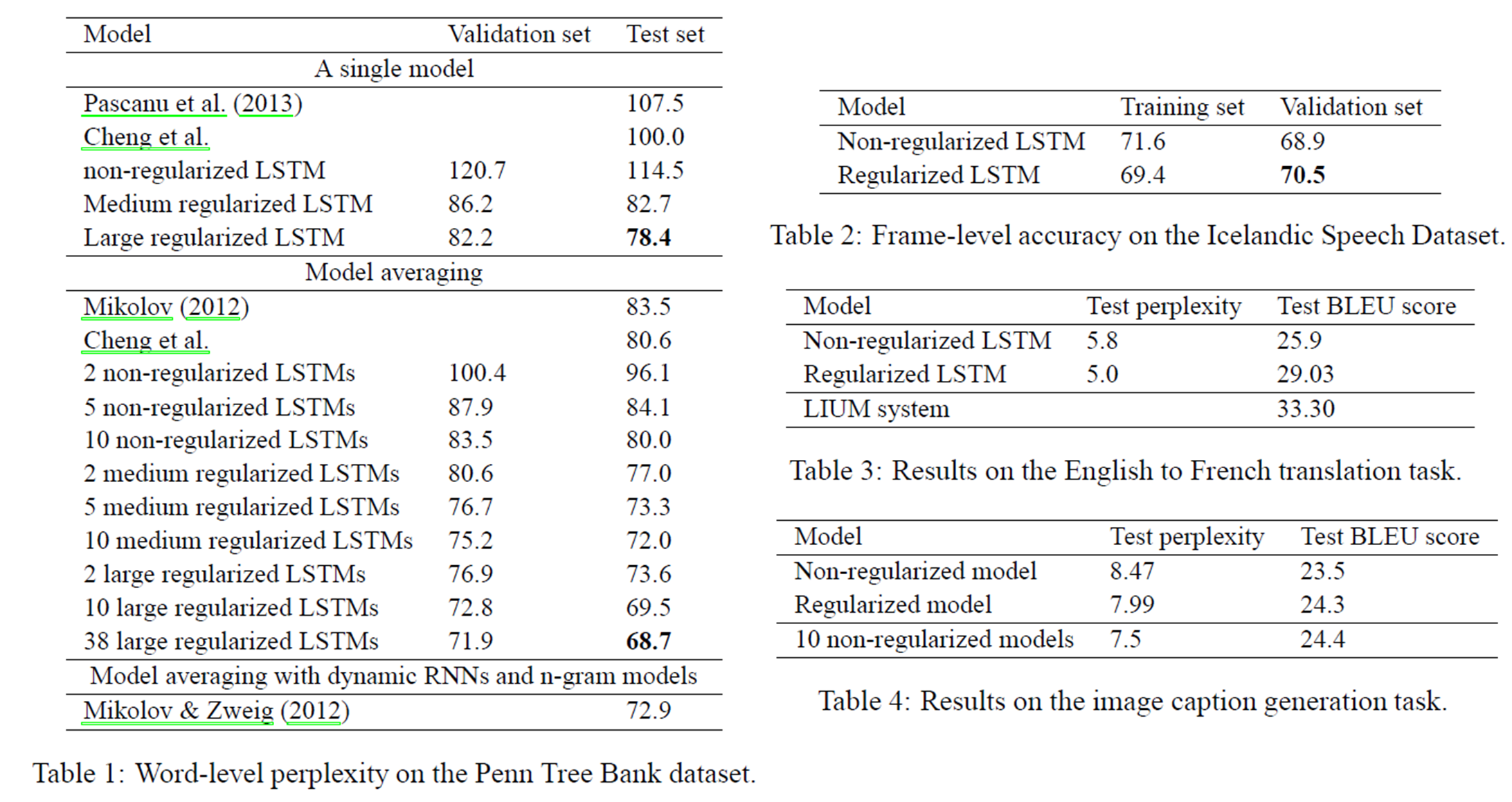
논문에서는 총 4개의 실험을 진행한다. Language Modeling (Penn Tree Bank - PTB dataset), Speech Recognition, Machine Translation 그리고 마지막으로 Image Caption Generation이 그것이다. 결과는 순서대로 아래 Table 1,2,3,4에 나열되어있다.
Summary of Recurrent Neural Network Regularization
- Motivation: Dropout을 RNN에 그냥 적용하면 성능이 좋지 않다
- Idea: Dropout을 모든 connection에 적용하는 대신 non recurrent connection에만 dropout을 적용하자