이번에 리뷰할 논문은 Google DeepMind가 NIPS 2013에 발표한 Deep Learning과 Reinforcement Learning을 결합한 Playing Atari with Deep Reinforcement Learning 이라는 논문이다. 그 전에도 DNN과 RL을 결합하려는 시도는 있었지만, 거의 사람이 플레이하는 수준으로 의미있는 수준까지 도달한 work은 이 work이 처음인듯 하다. 글을 시작하기 전에 먼저 이 논문에서 한 결과부터 살펴보자. Atari라는 게임 콘솔을 가지고 이 논문의 method를 적용한 결과이다. 2분 5초부터 시작되는 터널링 전략이 진짜 걸작이다.
충격적인 사실은 다른 hand-coding feature나 parameter 튜닝 없이 오직! vision data만 사용해서 이런 결과를 냈다는 사실이다. 빨간 공이 object고 빨간 판이 내가 움직이는거라는 기본적인 hand-craft feature 조차 없이 이런 결과를 냈다는 것이다. Deep leanring이 RL에서 뛰어난 성과를 보이지 못한 이유가 주로 데이터에 관련된 것이었음을 생각해보면 대단한 결과라고 할 수 있다. 최근에는 이 work을 기반으로 Image Attention (NIPS 2015) 이라고 부르는 work도 나온 것 같다. Image Attention 논문은 다음에 정리해보도록하겠다.
Background
이 논문은 RL 중에서도 MDP에 초점을 맞추고 있으며 (사실 MDP가 아닌 RL은 거의 없다고 봐도 무방하지만) 그 중에서도 model-free technique 중 하나인 Q-learning algorithm을 neural network를 통해 해결하고 있다. 이 글은 RL에 대해 어느 정도 기초적인 지식이 있다고 가정하고 쓸 것이기 때문에 조금 더 자세한 내용은 추후 작성할 RL 관련 포스트나 이 포스트나 다른 reference들을 참고하면서 읽으면 좋을 것 같다.
Reinforcement Learning을 위해서는 먼저 환경 $\mathcal E$을 정의해야한다. 이 논문에서는 Atari 에뮬레이터가 환경이 될 것이다. Atari 에뮬레이터 환경을 구성하는 요소는 action의 sequence들, observe하는 화면과 최종 reward (점수)가 될 것이다. 그림으로 표현하면 다음과 같은 식이다.
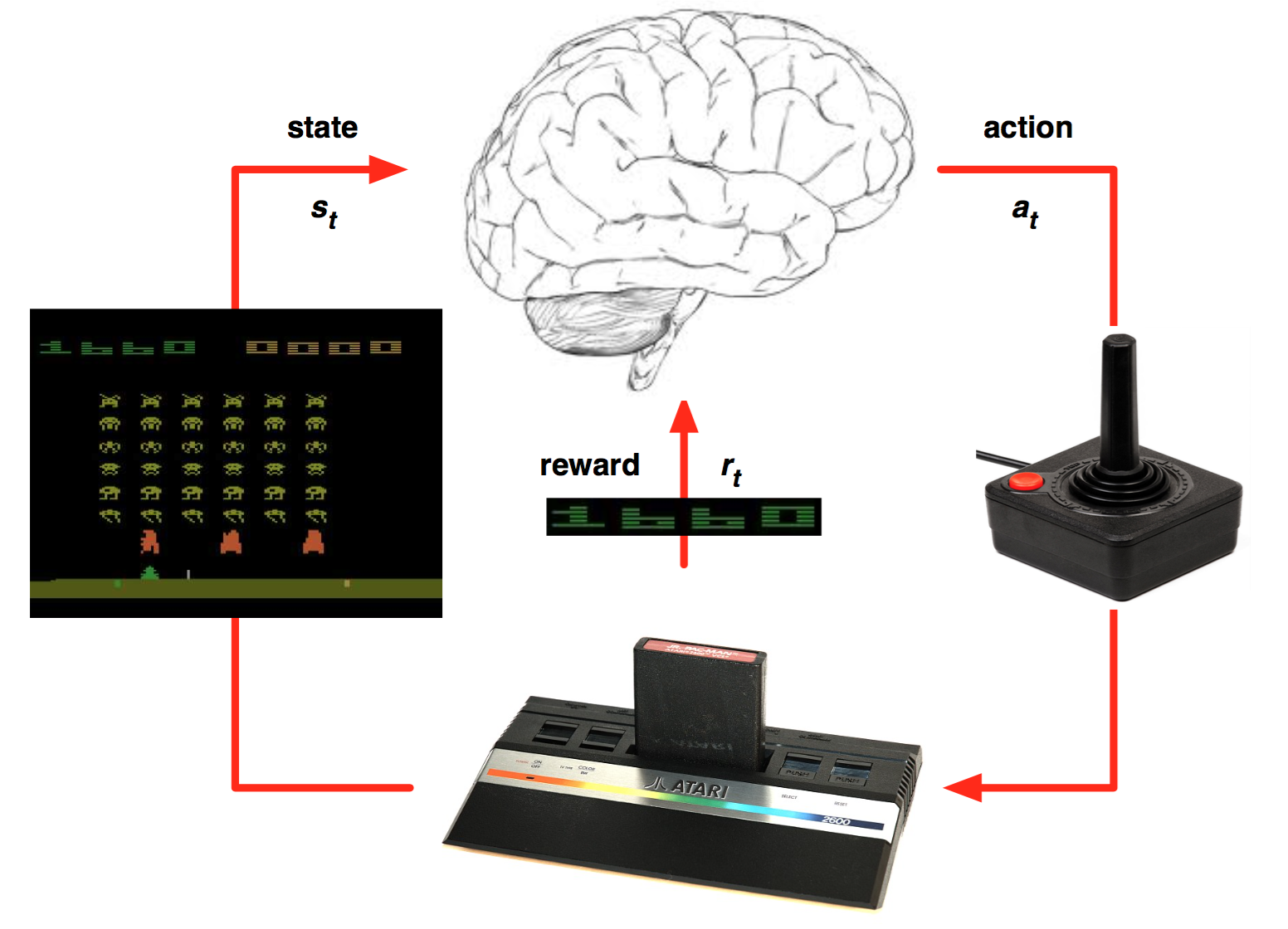
매 시간마다 agent는 legal game action $\mathcal A = \{1, \ldots, K\}$ 중에서 action $a_t$를 하나 선택한다. 예를 들어 아래 그림과 같은 컨트롤러의 버튼 중 어떤 버튼을 누를 거인지를 결정하는 것이다. 옆으로 움직이는 버튼, 기타 다른 버튼들 하나하나가 $\mathcal A$의 element이며, 그 중 하나가 action $a_t$가 되는 것이다.

게임을 하는 동안 컨트롤러의 버튼을 누르는 action들이 모이게 되면 현재 점수에 어떻게든 영향을 주게 되고, 그 결과로 최종 점수가 결정된다. 즉, Atari 게임 환경에서 reward $r_t$는 게임 score이며, 현재 내가 선택한 action은 바로 reward에 반영되는 것이 아니라 엄청나게 나중에 반영될 수도 있는 것이다.
또한 게임 조작을 통해 변화하는 것 중 우리가 관측할 수 있는 것은 실제 게임 화면의 pixel 값들 뿐이다 (이 논문에서는 time stamp $t$에서의 픽셀 값을 $x_t$라고 정의하였다). 때문에 이 논문에서는 vision 데이터를 사용해서 state를 정의하는데, state를 정의하는 방식이 상당히 재미있다. 간단하게 $x_t$를 state로 삼으면 될 것 같지만, 실제로는 화면 하나만 보고 알 수 있는 정보가 제한적이고 현재 상태를 정확하게 판단하기 위해서는 vision정보와 내가 행한 action을 포함한 과거 history들까지 모두 있지 않으면 안되기 때문에 이 논문은 state $s_t$를 action과 image의 sequence로 정의한다. 예를 들어 아래 스크린샷에서 공은 왼쪽으로 움직일까 오른쪽으로 움직일까? 만약 관성을 implement한 게임이라면 (움직이는 버튼에서 손을 떼도 조금 움직이는 게임이라면) 과연 play agent는 위로 올라가고 있을까 아니면 아래로 내려가고 있을까 그것도 아니면 멈춰있을까? 이렇듯 한 time stamp에 대한 vision 데이터로는 파악할 수 있는 데이터가 너무 제한적이기 때문에 모든 history가 반드시 필요하다.

다시 말해서, $s_t = x_1, a_1, \ldots, a_{t-1}, x_t$ 가 된다. 이런 방식으로 modeling을 하게 되면 policy 혹은 strategy를 learning할 때 모든 과거 sequence를 고려해서 strategy가 결정되게 된다. 게임은 언젠가 끝나게 되어있기 때문에 모든 $s_t$는 finite한 길이를 가지고 있으며 (비록 어마어마하게 크지만) $s_t$의 domain 역시 유한하다. 따라서 이 모델은 엄청나게 large하지만 어쨌거나 finite한 Markov dicision process(MDP)가 된다.
우리의 목표는 에뮬레이터에 agent가 어떤 strategy를 통해 게임을 조작하여, 최종적으로 게임이 끝났을 때 게임에서 가장 높은 점수를 획득하는 것이다. 즉, reward에 대한 수학적 정의만 있다면 이 문제는 간단한 optimization 문제가 된다. 게임은 보통 시간 마다 reward를 받는다. 하지만 일반적으로 시간이 오래 지날수록 해당 reward의 가치는 점점 내려가는데 이를 고려하기 위하여 discount factor $\gamma$가 정의된다. 시간 $t$의 reward를 t라고 한다면 time $T$에서의 discount factor를 고려한 future reward는 다음과 같이 정의한다.
$$R_t = \sum_{t^\prime=t}^T \gamma^{t^\prime-t} r_{t^\prime}.$$
Reward function을 정의했으니 Q-function (action-value function) 역시 정의할 수 있다. $\pi$를 $s_t$에서 $a_t$를 mapping하는 policy function이라하면, optimal Q-function $Q^*$는 다음과 같이 정의할 수 있다.
$$Q^*(s,a) = \max_\pi \mathbb E \big[ R_t \big| s_t = s, a_t = a, \pi \big]. $$
MDP에서는 이 optimal action value function 혹은 optimal Q-function 하나만 제대로 알고 있다면 언제나 주어진 state에 대해 가장 $Q^*$의 값을 크게 만드는 action을 고르는 간단한 policy만으로도 반드시 항상 optimal한 action을 고를 수 있다는 이론적 결과가 있기 때문에 Q-function은 매우매우 중요하다. 이 논문에서도 $Q^*$를 찾는 neural network를 만들어서 문제를 해결하고 있으니, Q-function에 대한 이해가 필수적이다.
다시 본문으로 돌아와서, Optimal Q-function은 Bellman equation이라는 중요한 특성을 따르게 된다. 이 equation을 intuition은 대충 이런식이다: seqeunce $s^\prime$의 다음 time stamp에서의 optimal Q-function $Q^* (s^\prime, a^\prime)$ 값이 모든 action $a^\prime$에 대해서 알려져 있다면, optimal strategy는 $r + \gamma Q^* (s^\prime, a^\prime)$의 expected value를 maximize하는 것이라는 것이다. 이를 수식으로 표현하면 다음과 같다.
$$Q^*(s,a) = \mathbb E_{s^\prime \sim \mathcal E} \bigg[ r + \gamma Q^* (s^\prime, a^\prime) ~\big|~ s,a \bigg].$$
많은 RL algorithm 들에서는 Q-function을 estimate하기 위하여 이 Bellman equation을 value iteration algorithm이라는 것을 통해 iterative update하여 구하게 된다. Value iteration algorithm에서는 매 $i$ 번쨰 iteration마다 다음과 같은 procedure를 수행하게 된다.
$$Q_{i+1} (s,a) = \mathbb E \bigg[ r + \gamma Q^* (s^\prime, a^\prime) ~\big|~ s,a \bigg].$$
이런 value iteration algorithm은 MDP에서 $Q_i \to Q^* \mbox{ as } i\to\infty$라는 것이 알려져 있다. 그러나 이런 방식은 이론적으로는 의미가 있을지 몰라도 실제로는 완전히 impractical한데, 이 과정을 모든 seqeunce에 대해 독립적으로 시행해야하기 때문이다. 따라서 보통은 action-value function을 다음과 같은 식으로 적절한 approximator를 사용하여 approximation한다.
$$Q(s,a;\theta) \simeq Q^* (s,a).$$
보통 linear function으로 approximation하지만, 간혹 non-linear function으로 모델링하는 경우도 있다. 예를 들어 deep network를 쓰는 방법이 있는데, 이 논문은 기존 방법들에 비해 RL에 적합한 Deep Network 모델을 제안하여 뛰어난 non-linear function approximator를 제안한다.
일반적으로 RL에 deep learning approach를 바로 적용했을 때 몇 가지 이슈가 생기게 되는데, 먼저 deep learning을 하기 위해서는 엄청나게 많은 hand labelled training data가 필요하지만, RL에서는 모든 state와 action에 대한 labelled data가 없기 때문에 이를 어떻게 handle해야할지를 모델에서 고려해야만한다. 또한 현재까지 연구된 많은 deep learning structure들은 data가 i.i.d.하다고 가정하지만, 실제 RL 환경에서는 state들이 엄청나게 correlated되어있기 때문에 제대로 된 learning이 어렵다. 예를 들어 위 핑퐁 게임 화면에서 한 프레임 더 지난 화면과 지금 화면은 정말 엄청나게 높은 correlation을 가지지만, standard feed-forward deep learning은 그것을 처리할 수 있는 모델이 아니기 때문에 문제가 발생한다. 이 논문은 그 문제를 experience replay라는 것으로 해결하는데, 자세한 내용은 다음 section에서 다루도록 하겠다.
Deep Q-Learning
앞에서 정의한 Q-function을 modeling한 network를 ($Q(s,a;\theta) \simeq Q^* (s,a)$, 이때 $\theta$는 weight나 bias 등 neural network의 model parameter들) 이 논문에서는 Q-network라고 부르고 있다. 만약 parameter가 $\theta$가 정해진다면, 우리는 state $s$와 action $a$를 Q-network에 넣어서 forward pass를 돌리게 되면 해당하는 Q-value를 얻을 수 있을 것이다. 따라서 parameter가 정해진다면 주어진 $s$에 대해 모든 $a$에서의 Q-value를 얻을 수 있고, 이를 통해서 $Q^*$의 값과 그것을 achieve하는 action $a^*$를 구하는 것도 가능해진다. 다시 말해서 이 Q-network를 올바른 방향으로 update하는 알고리즘을 design하기만 한다면 주어진 문제를 해결할 수 있는 것이다. 이 논문에서는 Q-network가 우리가 원하는 목적대로 train되도록 하기 위하여 i 번째 iteration에서 아래와 같은 loss function을 가지도록 design한다. 이 논문은 현재 Q-network가 항상 target Q-value에 가까워지도록 loss를 설정함으로써 마치 value iteration이 converge하듯 Q-network의 update가 converge할 때 까지 iterative algorithm을 돌리도록 하는 것이다. 이때 $y_i$는 iteration i의 target value이고, $\rho(s,a)$는 sequence $s$와 action $a$의 probability distribution이며, 이를 이 논문에서는 behaviour distribution이라고 정의한다.
$$L_i (\theta_i) = \mathbb E_{s,a\sim \rho(\cdot)} \bigg[ \big(y_i - Q(s,a;w_i) \big)^2 \bigg], $$
$$\mbox{where, }y_i = \mathbb E_{s^\prime \sim \mathcal E} \bigg[r + \gamma \max_{a^\prime} Q(s^\prime, a^\prime;w_{i-1}) ~\big|~ s, a \bigg]. $$
주의할 점은, optimization 과정에서 parameter $\theta$가 update되는 동안 loss function $L_i(\theta_i)$ 의 이전 iteration paramter $\theta_{i-1}$은 고정된다는 것이다. 이를 ‘freeze target Q-network’ 라고 부르는데, 이렇게하는 이유는 supervised learning과는 다르게, target의 값이 $\theta$의 값에 (민감하게) 영향을 받기 때문에 stable한 learning을 위하여 $\theta$값을 고정하는 것이다. 이건 아래에서 조금 더 자세하게 설명하도록 하겠다. 이제 loss function을 정의되었으므로 gradient값만 있다면 그 값을 사용해서 backpropagation을 돌리면 쉽게 update할 수 있다. 이 network의 loss의 gradient는 다음과 같이 구할 수 있다.
$$\nabla_{\theta_i} L_i (\theta_i) = \mathbb E_{s,a\sim \rho(\cdot); s^\prime \sim \mathcal E} \bigg[ \big( r + \gamma \max_{a^\prime} Q(s^\prime, a^\prime; \theta_{i-1}) - Q(s,a;\theta_i) \big) \nabla_{\theta_i} Q(s,a;\theta_i)\bigg]$$
하지만 이렇게 build한 Deep RL을 바로 사용할 수는 없고, 아래와 같은 몇 가지 이슈들을 처리해야한다.
- Deep Learning은 데이터가 i.i.d.하다고 가정하지만 실제 RL input의 데이터는 sequential하고 highly correlated 되어있다.
- Policy 변화에 따른 (이 경우는 w의 변화에 따른) Q-value의 변화량이 너무 크기 때문에 policy가 oscillate하기 쉽다.
- 위와 같은 세팅에서는 reward와 Q-value의 값이 엄청나게 커질 수 있기 때문에 stable한 SGD 업데이트가 어려워진다.
첫 번째 이슈는 이미 전 문단에서 간단하게 언급했었으니 생략한다. 두 번째 문제도 크게 어렵지 않게 생각할 수 있는데, 게임을 하는 방식을 아주 조금만 바꾸더라도 게임의 결과가 완전히 크게 바뀌기 때문에 이런 현상이 발생한다. 핑퐁 게임에서 움직이는 속도를 조금 늦춘다거나 했다가는 바로 한 점을 잃게 될 것이다. 또한 앞에서 설명한 것 처럼 supervised learning과는 다르게 target의 값이 parameter에 영향을 아주 민감하게 받기 때문에, 이 값을 고정해주는 과정이 필요하다. 마지막 조건은 좀 practical한 이슈인데, Q-value의 값이 얼마나 커질지 모르기 때문에 stable update가 힘들 수도 있다. 이 논문에서는 다음과 같은 세 가지 방법으로 각각의 issue를 handling한다
- Experience replay
- Freeze target Q-network
- Clip reward or normalize network adaptively to sensible range
이 중에서 두 번째 idea는 이미 설명했고 (update하는 동안 target을 계산하기 위해 사용하는 paramter를 고정), 세 번째 idea는 reward의 값을 [-1,0,1] 중에서 하나만 선택하도록 강제하는 아이디어이다. 즉, 내가 100점을 얻거나 10000점을 얻거나 항상 reward는 +1 이다. ‘highest’ score를 얻는 것은 불가능하지만, 이렇게 설정함으로써 조금 더 stable한 update가 가능해진다. 그리고 그와는 별개로 모든 게임에 적용가능한 DQL을 learning할 수 있다는 장점도 있다. 실제로 실험에서는 모든 게임을 단 하나의 네트워크로만 learning해서 기존의 모든 방법을 beating한다.
그럼 이제 마지막으로 이 논문의 핵심 아이디어라고 할 수 있는 experience replay에 대해 살펴보자. Experience replay는 agent의 experine를 각 time stamp마다 다음과 같은 튜플 형태로 메모리 $\mathcal D = e_1, \ldots, e_N$ 에 저장한 후 이를 다시 사용하는 것이다.
$$e_t = (s_t, a_t, r_t, s_{t+1}).$$
Experience replay는 이렇게 experience $e_t$를 메모리 $\mathcal D$에 저장해두었다가, 일부를 uniformly random하게 sample하여 mini-batch를 구성한 다음 parameter $\theta$를 mini-batch에 대해 backpropagation으로 update하는 과정을 의미한다.
Experience replay를 사용함으로써 data의 correlation을 깰 수 있고, 조금 더 i.i.d.한 세팅으로 network를 train할 수 있게 된다. 또한 방대한 과거 데이터가 한 번만 update되고 버려지는 비효율적 접근이 대신에, 지속적으로 추후 update에도 영향을 줄 수 있도록 접근하기 때문에 데이터 사용도 훨씬 효율적이라는 장점이 있다. 실제로 실험에서는 메모리 용량의 한계 때문에 bucket을 $N$으로 고정하고, FIFO 형태로 저장을 한 모양이다.
Experience replay가 끝난 후 agent는 action을 $\epsilon$-greedy policy라는 것을 사용해 선택하고 실행한다. 이 방법은 action을 $\epsilon$의 확률로 random하게 고르거나 $1-\epsilon$의 확률로 MDP의 optimal action selection criteria인 $a_t = \arg\max_a Q^*(s_t, a;\theta) $로 고르는 policy를 의미한다.
참고로, arbitrary length의 input을 다루는 것이 general feed-forward network에서는 어렵기 때문에, 이 논문에서는 function $\phi$라는 것을 정의해서 모든 $s_t$의 length를 fix한다. 이 알고리즘을 수식적으로 기술하면 다음과 같이 기술할 수 있다.

Equation 3은 위에서 증명한 gradient 값이고, 함수 $\phi$는 다음과 같다: 주어진 history 중에서 가장 마지막 4개의 frame을 stack으로 쌓는 것. 이때 각각의 frame은 원래 128색 210 by 160 픽셀으로 구성되어있지만, gray-scale로 만들고 110 by 84로 down sampling한 후 84 by 84로 크롭한다. 이때 크롭을 하는 이유는 주어진 툴에서 정사각형 사진만 GPU 연산이 되기 때문이라고..
이렇게 experience replay라는 아이디어를 사용한 DQL은 몇 가지 이점이 있다.
- 각각의 experience가 potentially 많은 weight update에 reuse되기 때문에 experience를 weight update 한 번에만 사용하는 기존 방법보다 훨씬 data efficiency하다.
- 두 번째로, mini-batch를 만드는 sampling 과정을 통해 데이터들 간의 high correlation을 효율적으로 관리하고, 이를 통해 보다 효율적인 update를 할 수 있다. 이 방법은 random하게 sample을 뽑아서 mini-batch로 구성하기 때문에 이런 high correlation을 break해서 update의 효율성을 높이기 때문이다.
- 마지막으로 이 방법을 통해 parameter를 update하게 되면 다음 training을 위한 data sample을 어느 정도 determine할 수 있다. 예를 들어서 내가 지금 오른쪽으로 움직이는 쪽으로 action을 고른다면 다음 sample들은 내가 오른쪽에 있는 상태의 sample들이 dominate하게 나올 것이라고 예측할 수 있다. 따라서 이 방법을 통해 training을 위한 다음 데이터를 무작정 뽑는 것이 아니라 현재 action을 고려하여 효율적으로 뽑을 수 있다.
몇 가지 주의점이라면 freeze target Q-network, 혹은 off-policy가 반드시 필요하다는 점 정도가 있겠다. 한계점으로는 메모리의 한계 때문에 앞에서 말한 것처럼 모든 history를 저장하지 못한다는 점과, uniform sampling을 사용하기 때문에 모든 과거 experience가 동일한 weight를 가진다는 점이다. 이 논문에서는 조금 더 wise한 sampling을 하게 되면 성능 향상이 있을 수도 있다고 언급하고 있다.
Model Architecture of DQL and Experiment
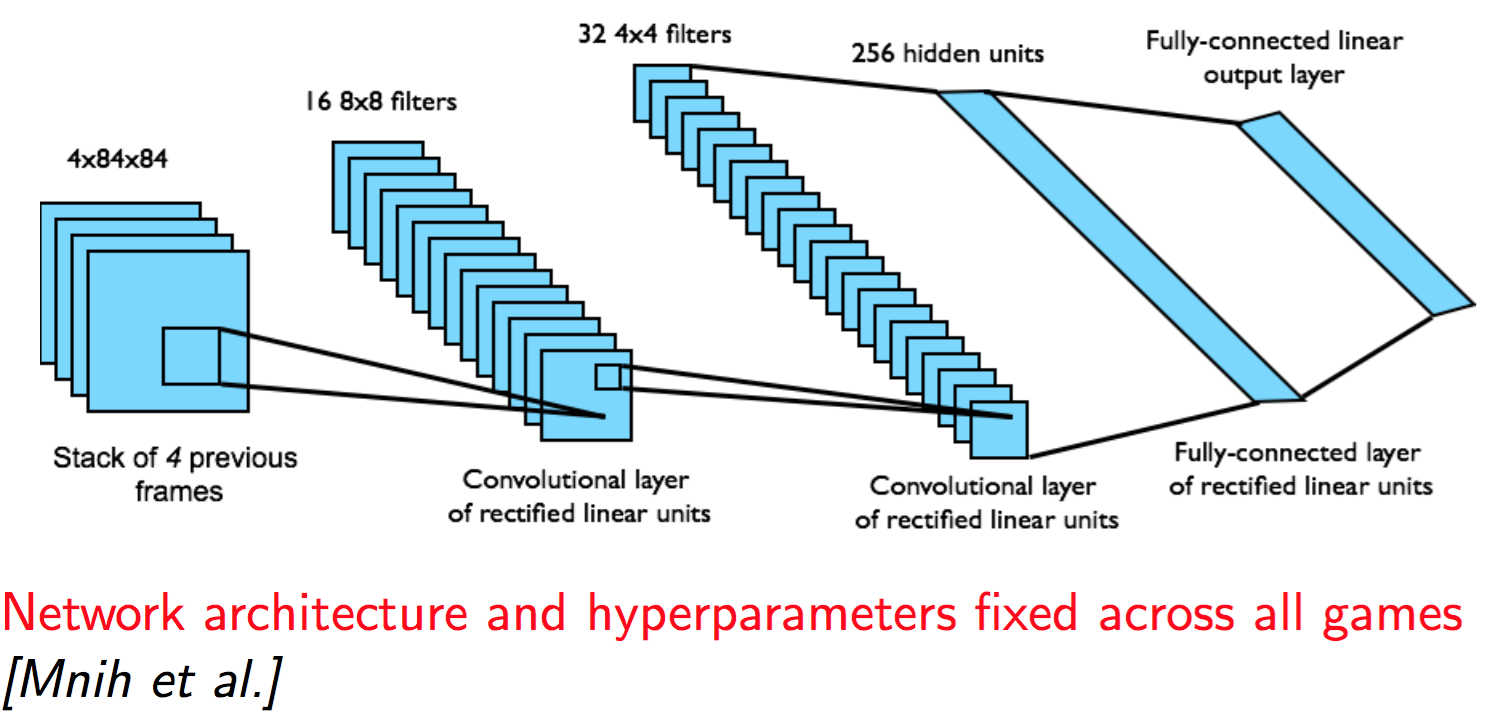
이제 구체적으로 어떤 neural network 모델을 사용해 learning을 하게 될지 알아보자. 항상 관심있게 살펴봐야 할 내용은 (1) input data는 무엇인가 (2) output data는 무엇인가 (3) 구체적인 network 구조는 어떻게 되는가 정도가 있겠다. 이 논문에서는 input으로 $\phi(s_t)$를 받고, output으로 가능한 모든 action에 대한 Q-value를 출력한다. 즉, 버튼이 4개 있다면 output은 4개이고, 12개 있다면 output은 12개이다. 실제 논문에서는 게임 종류에 따라 action을 4개에서 18개 사이에서 고른 것 같다. 이렇게 모델을 고르게 되면 $Q^*$를 단 한번의 forward pass 만으로 구할 수 있다는 장점이 있기 때문에 이 논문에서는 이러한 방법을 선택하였다. 구체적인 네트워크는 CNN을 사용한다. 인풋 데이터는 $\phi(s_t)$를 넣는다고 했으므로 84 by 84로 크롭한 후에 4개의 history를 stack으로 쌓은 데이터가 들어오게 된다. 그러니까 대충 다음과 같은 식이다.
이 네트워크를 사용한 자세한 실험 결과는 다음 표에 나와있다. 각각의 숫자는 모두 reward를 의미하기 때문에 값이 클 수록 좋은 결과이다.
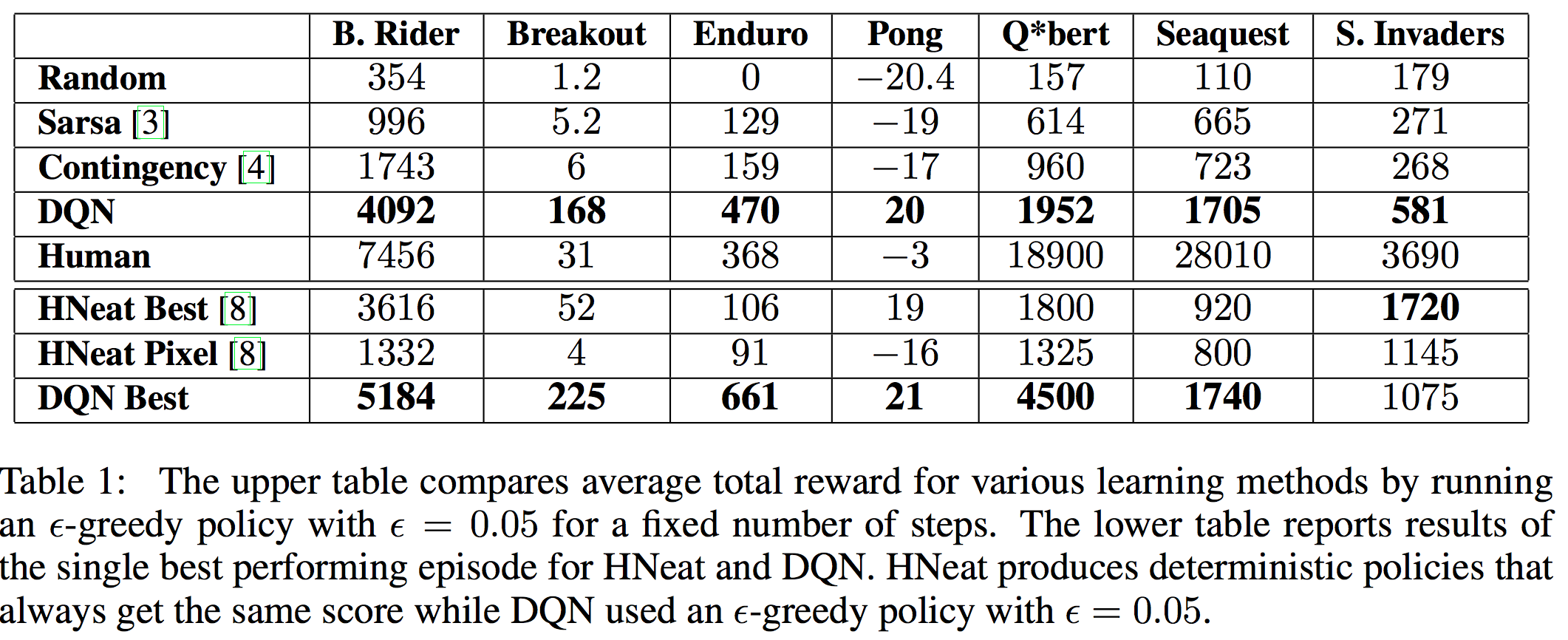
Breakout, Enduro, Pong은 심지어 사람보다도 좋은 것을 알 수 있고, Space Invaders를 제외하면 기존 모델들보다 best 뿐 아니라 avg 까지 뛰어난 것을 볼 수 있다. 논문에서는 Q*bert, Seaquest, Spae Invaders 등의 게임에서 사람의 performance에 한참 미치지 못하는 이유로 이 게임들은 전략이 엄청나게 긴 time scale로 필요하기 때문에 조금 더 challenge한 문제라고 주장하고 있다. 아마 하드웨어의 발달과 모델의 발달로 언젠가는 극복할 수 있을 것으로 보인다.
Summary of DQL
- 문제 정의 자체가 흥미롭다. 특히 state space를 sequence of iamges and action으로 구성했다는 점이 흥미롭다.
- State에 대한 hand-craft feature가 전혀 없다. 오직 이미지 sequence만을 사용해서 CNN으로 feature를 자동으로 만들어내는 방법으로 이를 해결하고 있다는 점이 흥미롭다.
- Q-function을 learning하는 neural network를 구성하였는데 몇 가지 stable update를 위하여 ‘off-policy’를 사용하고, ‘experience replay’ 기법을 사용한다.
- Experience replay는 매 시간마다 experience tuple $e_t$를 메모리에 저장하고, 메모리에서 $e_t$를 uniformly sample하여 뽑아 mini-batch를 구성하고 이를 (off-policy를 적용한 채로 혹은 target network를 freeze하고) 사용해 parameter를 update하는 아이디어이다.
- 서로 다른 Atari 게임 7개에 대한 policy를 learning하기 위해 단 하나의 neural network만을 사용했고, 그 결과가 기존 결과를 outperform한다.