본 포스팅은 단기강좌 인터넷 속의 수학의 강의 들을 요약하는 포스트입니다.

Recall: Machine Learning

이전의 많은 포스트 들에서도 설명했듯이 Machine Learning은 데이터를 통해 새로운 시스템을 만드는 것을 의미한다. 그렇다면 굳이 사람이 아니라 기계가 이런 일을 해야하는 이유가 있을까? 무엇보다 기계는 사람보다 단순 계산을 훨씬 빠르게 할 수 있다. 간단한 예를 하나 들어보자. 페르마 숫자라는 문제가 있다.

$$ {F_n} = 2^{2^n} +1 $$

이 숫자는 위와 같이 표현이 되는데, 페르마는 모든 n에 대해서 이 숫자가 소수라는 주장을 하였다. 그러나 100년 뒤 오일러가 이의 반례를 찾아냈다.

$$ {F_5} = 2^{2^5} + 1 = 2^{32} +1 = 4294967297 = 641 * 6700417 $$

사람이 이를 증명하는 데에 100년이라는 시간이 걸렸지만, 컴퓨터를 사용하면 이 문제는 고작 몇 분안에 끝나는 간단한 문제이다. 이런 문제에서 컴퓨터 혹은 기계를 사용하는 것이 매우 효율적인 것이다. 다시 Machine Learning으로 돌아가보자. Machine Learing algorithm은 주어진 training data에서 특정한 시스템을 만들고 각종 model parameter들을 optimize하여 주어진 training data에 가장 잘 들어맞는 system을 만든다. 이런 과정을 위해서는 이런 optimize problem이 reasonable한 시간 안에 풀 수 있는 문제인지 그렇지 않은 문제인지 반드시 알아야만 한다. 만약 한 문제를 optimize하는데에 엄청 오랜 시간.. 예를 들어서 몇십만년 단위의 시간이 걸린다면 실전에서 사용할 수 없을 것이다.

과연 컴퓨터로 풀 수 있는 문제란 무엇이 있을까? 컴퓨터는 Turing에 의해 1936년에 처음 제시가 되었고 (Turing Machine) 이 덕분에 지금까지 하드웨어 문제에 불과했던 성능에 관련된 문제가 수학적인 문제로 치환될 수 있었다. 또한 1971년 Computational classes (NP complete) 가 Cook에 의해 define되었다. 여기에서 정의된 P와 NP problem을 사용하면 우리가 처음 제시한 질문: 이 문제를 컴퓨터로 풀 수 있는가? 에 대한 질문에 답을 할 수 있는 것이다.

다음에 대한 설명을 하기 전에 먼저 P와 NP problem에 대해 잠시 설명하도록 하겠다. 먼저 P는 금방 문제의 정답을 찾을 수 있는 문제이다. 또한 NP는 해답이 있을 때 이 해답이 맞는지 아닌지 verify할 수 있는 문제를 뜻한다. 예를 들어 어떤 주어진 여러 개의 Path 중에서 특정한 path를 찾는 문제는 P problem이다. 또한 NP problem은 path가 있을 때 그 path를 따라갈 수 있는가에 대한 문제가 되는 것이다. 이 두 개의 문제에 해당하지 않는 문제도 엄청나게 많으며, 재미삼아 말해주자면, P이면 NP인가? 라는 질문은 Seven Millennium Prize Problems 중 하나일 정도로 수학에서 상당히 중요한 영역을 차지하고 있다.

P problem의 대표적인 예는 Convex Optimization이다. Convex Optimization은 mimimum value를 찾는 문제 중에서 매우 특수한 경우를 의미하며, 함수가 convex하고 domain 역시 convex한 경우를 의미한다. 간단하게 생각하면 convex와 ‘볼록하다’ 가 같은 말이며, convex function이란 모든 구간에서 볼록한 함수를 의미한다. (Convex Optimization에 대해서는 나중에 더 자세한 포스팅으로 설명을 할 수 있도록 하겠다.) 간단히 예를 들어보면

위의 그림에서 아래 함수는 일부 구간에서 볼록하지 않기 때문에 convex하지 않고 위 함수는 convex하다. 위의 그림을 보면 알 수 있듯, convex function에서는 local한 minimum value만 찾더라도 global한 mimimum값을 찾을 수 있다. 때문에 Convex optimization은 optimization 중에서도 매우 특수한 경우이며 P, NP problem 중에서 P에 속하는 문제이다. 이를 수식적으로 표현해보면

$${minimize}\quad{f(x)}$$ $${subject}\,{to}\,{x} \in D \subseteq {R^n}$$

으로 표현하는 것이 가능하다. Netflix 알고리듬에서 언급하게 될 3개의 알고리듬 중에서 Baseline predictor와 Matrix factorization 알고리듬에서 이런 Convex Optimization을 활용하게 된다.

Recall: Netflix Recommendation Problem

Netflix problem의 목적은 간단하다. Netflix Matrix라는 user와 movie의 조합으로 이루어진 Matrix에서 아직 알려지지 않은 부분의 값을 유추하는 것이다. 이 문제에 대한 설명은 지난번에 적은 글에 자세히 적혀있으니 생략하도록 하겠다. 그렇다면, 새로운 알고리듬이 더 좋은 알고리듬인지 아닌지 어떻게 판단할 수 있을까? 여러가지 방법이 있을 수 있지만, Netflix에서는 RMSE (Root Mean Squared Error) 를 정의한다. RMSE는 $\sqrt{MSE} = \sqrt{\frac 1 n \sum_{i=1}^n ( \hat{X_i}-X_i )^2}$로 표현이 가능하며, 쉽게 생각하면 예측치가 실제 값과 얼마나 차이가 나는지를 측정하는 역할을 한다고 생각하면 간단하다. 즉, Netflix의 Recommendation problem은 Netflix Matrix에서 알려져 있는 entry를 사용해 training set과 problem set을 만들고 RMSE를 계산해서 그 RMSE를 최대한 낮추는 문제인 것이다. 이 글에서는 이런 RMSE의 값을 10% 줄이기 위한 3가지 알고리듬: Baseline Predictor, Neighborhood method, Matrix Factorization에 대해 다루게 될 것이다.

Algorithm 1: Baseline Predictor

첫 번째 알고리듬은 Baseline Predictor이다. 이 알고리듬은 각각의 영화 혹은 사람마다 기본적으로 정해진 Baseline이 존재한다는 가정에서부터 시작된다. 즉, 각각 영화마다 평점이 높은 영화가 있을 수도 있으며. 또 평점을 잘 주는 사람이 있을 수도 있고 짜게 주는 사람도 있을 수 있다. 또한 비교적 popular 한 영화라면 rating이 높을 것이고, 이 사람이 이전에 준 rating의 값의 평균이 낮다면 앞으로 줄 rating의 값 또한 작을 것이라는 가설을 세울 수 있을 것이다. 그렇다면 이런 baseline을 사람에 대한 혹은 영화에 대해서 각각 만들 수 있을 것이며 이를 모으면 vector로 표현하는 것이 가능할 것이다. $b_i$를 movie에 대한 baseline, $b_u$를 user에 대한 baseline이라고 가정하고, 이 baseline이 높으면 rating을 잘 받는 영화 / 잘 주는 사람 이라고 생각하자. 그렇다면 $$\hat r_{ui} = {\overline r} + b_u + b_i$$ 로 정의한다면, baseline을 찾는 문제는 $${minimize}\,\sum {(r_{ui} - \hat r_{ui})^2} $$ 을 만족하는 $b_u$와 $b_i$를 찾는 문제로 바꿀 수 있다. 그리고 여기에서 가장 중요한 점은 이것이다. 이 문제는 Convex optimization으로 풀 수 있다는 것이다.

Baseline Predictor는 기존의 데이터를 가장 잘 설명할 수 있는 model parameter를 찾는 문제이며 성능이 아주 썩 좋은 편은 아니지만 random guessing보다는 훨씬 좋으며 어느 정도의 가중치를 줄 수 있다는 장점이 존재한다. 특히 temporal model과 결합하여 baseline predictor를 사용하면 꽤 강력한 결과를 얻을 수 있는데, Baseline Predictor with Temporal Models는 User의 rating은 day에 dependent할 수 있다는 가정을 깔고 movie의 trend가 시간에 따라 변한다고 가정한다. 그리고 이에 대한 적절한 변수를 시간마다 주고 $b_u(t),\,b_i(t)$를 가장 잘 설명할 수 있는 baseline의 값을 찾음으로써 시간에 대한 정보까지 고려할 수 있는 알고리듬을 설계하는 것이 가능한 것이다.

그러나, 기본적으로 parameter를 fitting하는 문제이기 때문에 Overfitting problem이 발생할 수 있다. Overfitting problem이란 현재 parameter들이 training data에 너무 optimization되어 오히려 future data에 대해서는 값이 제대로 맞지 않는 경우를 의미한다. 이는 전체 데이터가 아닌 일부의 데이터만 봤기에 생길 수도 있는 문제이며 data에 noise가 끼어 noise까지 fitting이 되었었을 수도 있다. 아무튼 overfitting problem은 현재에 너무 과도하게 집중하면 미래 data를 설명하는 데에 문제가 생길 수 있다는 것을 의미한다. Baseline Predictor에서 Model parameter를 너무 optimize시키면 지금까지의 known data에는 정말 잘 맞지만, test data에서는 error가 엄청 커질 수도 있는 것이다. 이를 막기 위해서 위에서 제시했던 minimzation problem을 $${minimize}\,\sum {(r_{ui} - \hat r_{ui})^2 + \lambda (\sum_u {b_u}^2 + \sum_i {b_i}^2)} $$ 처럼 $\lambda$와 관련된 추가적인 term을 추가한 다음 풀게 된다면, overfitting문제가 어느 정도 해결된다. 여기에서 overfitting을 막기 위해 사용한 $\lambda$가 증가하게 되면 점점 test data error가 떨어지다가 어느 정도 지나면 test data error가 다시 increase 된다. 따라서 적절한 $\lambda$를 선택하는 것도 매우 중요하다는 것을 알 수 있다.

Algorithm 2: Neighborhood Method

지난 포스트에서도 설명했던 것 처럼 이 알고리듬에서는 각각의 movie마다 movie 간의 유사도 정보를 가지고 있다고 가정하고 각각의 movie i와 j마다 $d_{ij}$라는 distance term을 정의하여 그 distance를 통해 얼마나 유사한지를 판별하게 된다. 즉 이 아이디어는 rating을 user가 영화 i를 좋아했으면 j도 좋아하지 않겠느냐.. 라는 idea를 기반으로 measure를 하게 된다. 이 알고리듬에서 distance function은 $$ d_{ij} = \frac{({r_i} * {r_j})}{(|r_i| * |r_j|)} $$ 위와 같이 정의한다. 이 때 $r_i$와 $r_j$는 모든 user의 movie rating을 모아둔 vector이다. 즉, $r_i = [2, 1, 3, 4, …]$ 등으로 표현된다는 것이다. 이때 임의의 두 vector사이 unknown factor가 다를 수 있으므로 두 vector에서 모두 알고 있는 값들을 모아 reduced form을 구해서 이 값을 계산하게 된다고 한다. distance가 두 벡터의 내적을 2-norm으로 나눈 것으로 정의가 되기 때문에 $d_{ij}$는 두 vector 사이 angle에 cosine을 취한 값이 된다. 즉, 두 벡터가 가까우면 가까울 수록 1에 근접해지고 멀어질 수록 값이 작아지게 된다. 즉, 이렇게 거리를 정의함으로써 두 벡터 간의 유사성이 얼마나 되느냐를 측정하는 척도가 될 수 있는 것이다.

NH method는 이 알고리듬 자체만 사용하게 되었을 때 결과가 그닥 좋지는 못하다. 그러나 Baseline Predictor랑 같이 결합해서 사용할 수 있으며 Baseline predictor를 계산하고 알고 있는 값과의 error를 계산하고 이 에러 값을 사용해서 NM을 사용하면 훨씬 결과가 좋게 나오게 된다. 이렇게 사용하기 위해서는 $\hat r_{ui} = \sum \frac {(d_{ij} * r_{ij})} {\sum (d_{ij})}$ 와 같은 형태로 r을 정의하고 predict를 하게 된다. 이 경우 영화의 개수가 많아질수록 연산량이 어마어마하게 늘어나기 때문에 이 알고리듬은 모든 영화에 대해 전부 다 적용하는 것이 아니라 top 50 movie 중에서 i와 similar한 movie를 일부 골라서 적용한다고 한다.

Algorithm 3: Matrix Factorization

만약 알려진 거대한 Matrix가 있을 때 이를 더 작은 Matrix의 multiplication으로 표현할 수 있다면 우리는 더 적은 값을 measure해서 전체 값을 추측할 수 있을 것이다. 이것이 Matrix Factorization의 기본 아이디어이며, 이 알고리듬은 성능이 매우 뛰어나서 다른 알고리즘 없이도 8% 정도까지 개선이 가능하다고 한다.

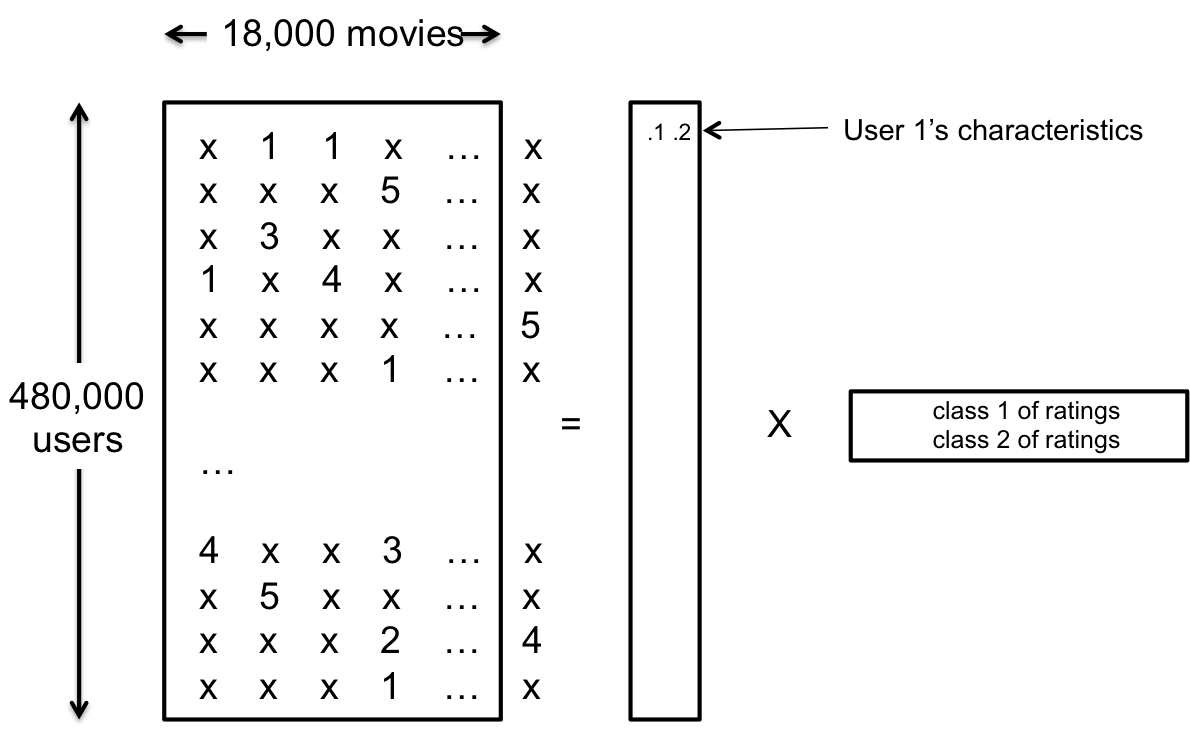
우리의 문제에서 각각의 Matrix를 R, P, Q라고 정의하자. 그리고 P와 Q 각각의 row의 개수와 column의 개수를 k라고 하자. 그렇다면 R은 480000 by 18000, P는 48000 by k, Q는 k by 18000 Matrix일 것이며, R = PQ가 될 것이다. 당연히 k의 값이 클 수록 낮은 에러로 원래의 데이터를 복구하기 쉬워지겠지만, k가 커질수록 overfitting issue가 존재하게 될 것이다. 실제로 Netflix에서는 약 20정도의 k를 사용한다고 한다. 당연한 얘기지만 실제로는 P, Q가 존재하지 않을 수도 있다. 따라서 이 문제는 아래와 같이 치환이 가능하다. $${minimize_{PQ}}\quad{|R-PQ|^2} = {minimize_{PQ}}\quad{(r_{ui} - p_u q_i)^2} $$ 이 문제는 P인가? 불행히도 이 문제는 함수 $f(P,Q)=|R-RQ|^2$ 자체가 convex가 아니기 때문에 Convex optimization problem이 아니며, P역시 아니다. 대신 이 문제를 convex optimization으로 근사하는 방법이 가능하다.

첫 번째 방법은 $minimize |R - PQ|$ 를 $minimize |R - A|^2 \hskip 1em where \hskip 0.3em rank(A) = k… $ 로 바꾸는 것이다. $|R-A|^2$은 convex function이기 때문에 convex optimization으로 푸는 것이 가능해 보인다. 그런데 domain인 rank(A) = k가 convex set이 아니기 때문에 이 문제는 불행히도 convex optimization은 아니다. 따라서 이를 가장 유사한 convex optimization problem으로 바꾸면, rank(A) = k라는 조건 대신에 ‘sum of singular values of A is at most h’ 라는 조건으로 문제를 풀면 된다. 이는 정확히 같은 조건은 아니고 거의 유사한 조건이다. 이렇게 문제를 non convex optimization에서 convex optimization으로 근사해서 원래 문제의 답을 추측하는 것이 가능한 것이다.

또 하나의 방법은 $minimize_{P,Q} |R-PQ|^2$ 을 푸는 것이다. 이 때 $f(P,Q) = |R-PQ|^2$은 convex function은 아니지만, P를 constant로 두면 Q에 대해 convex하고 Q를 constant로 두면 P에 대해 convex해지게 된다. 이를 bi convex라고 하며 둘 모두에 대해 convex하면 joint convex라고 한다. 아무튼 이제 이 방법 두 개를 모두 사용해서 Q를 고정하고 가장 잘 설명하는 P를 찾고, P를 고정하고 가장 잘 설명하는 Q를 찾는 과정을 반복적으로 왔다갔다 하면서 값을 찾는다. 이 방법을 이론적으로 분석하는 것이 엄청 어렵고 힘들어서 논문으로 많이 나오지는 않았지만 실전에서 엄청 많이쓰는 방법이다. 앞서 설명한 방법보다 이 방법이 더 성능도 잘 나온다. 최근 [Sujay et al. 2013] 에서 앞서 언급한 approach보다 이 approach가 좋은지는 모르겠지만 최소한 나쁘지 않다라는 것을 증명하였다고 한다. (구체적으로는 global optima convergence condition for R을 증명하였다고 한다.)

Summary and Questions

마지막으로 NH와 MF에 대해 잠시 비교해보자. NM은 local structure를 찾아서 recommendation problem을 풀겠다는 컨셉이고 MF는 global structure를 찾아서 recommendation problem을 풀겠다는 컨셉이다. 당연히 local한 solution보다 global한 structure를 찾는 컨셉이 더 정확할 것이다. 실제로 다른 알고리듬 하나도 없이 MF만 적용을 해봐도 Cinematch에 비해 8% 정도 improved 된 결과를 취할 수가 있게 된다. 하지만 역시 맨 처음 제시되었던 10%를 달성하려면 BP를 적용한 NH와 MF 둘을 잘 combine해야만 달성이 가능하다.

이런 알고리듬들에 대해서 몇 가지 Further Questions이 있을 수 있을 것이다.

• R = PQ를 풀기 위한 R의 entries 숫자는 얼마나 될 것인가
• MF를 더 빠르게 design할 수 있겠느냐, 더 나은 다른 algorithm도 있을 수 있겠느냐..
• NM과 MF를 같이 조합했을 때 왜 결과가 좋은 이유가 무엇이냐, 이론적인, mathematical answer 를 줄 수 있느냐

등의 question 들이 있을 수 있으며 이와 관련된 많은 연구가 활발하게 진행되고 있다고 한다.