본 포스팅은 단기강좌 인터넷 속의 수학의 강의 들을 요약하는 포스트입니다.

Review of last post

지난 포스트에서는 전반적인 강의의 개요 및 간단한 Network Problem들에 대해 다뤘다. 특히 그 중에서 밀그램의 편지 실험에 대해 다시 한번 살펴보자. 이 실험은 사람과 사람 사이의 사회적 거리를 측정하기 위한 실험이다. 여기에서 사회적 거리 혹은 social distance는 우리가 흔히 ‘distance’라는 컨셉에서 쉽게 생각할 수 있는 유클리언 distance와는 조금 다른 개념인데, 유클리언 distance가 지리적, 공간적인 거리의 개념이라면 social ditance는 내가 이 사람과 얼마나 가까우냐에 대한 얘기이다. 즉, 내가 미국에 유학가있는 친구와 유클리언 거리는 무지막지 멀지만 사회적거리는 엄청 가깝고, 옆 연구실의 학생분들은 유클리언 거리는 매우 가깝지만 안타깝게도 사회적 거리는 엄청 먼 셈이다. 구체적으로 social distance를 정의해보자. 이 값은 social network 위에서 내 node에서 다른 목표 node로 이동할 때 이동해야하는 총 거리를 의미한다. 즉, 밀그럼의 실험에서 실험 참가자들의 평균적인 사회적 거리는 약 5 정도가 되는 것이다. (이전에도 언급했듯, Facebook에서 같은 실험을 해보면 4.74가 나온다.)

자, 다시 한번 이전에 설명했던 실제 네트워크, 허브라는 개념 등에 대해서 생각해보자. 이렇게 전혀 상관없어 보이는 사람들 사이의 사회적 거리가 짧게나오는 이유는 사회적 네트워크의 토폴로지가 (그래프의 모양이) 독특하기 때문이다. 아래 그림을 봤을 때 구조적으로 멀어 보이는 지점을 이어주는 엄청나게 긴 장거리 연결 링크 (long-range link)가 존재한다는 것을 알 수 있다.

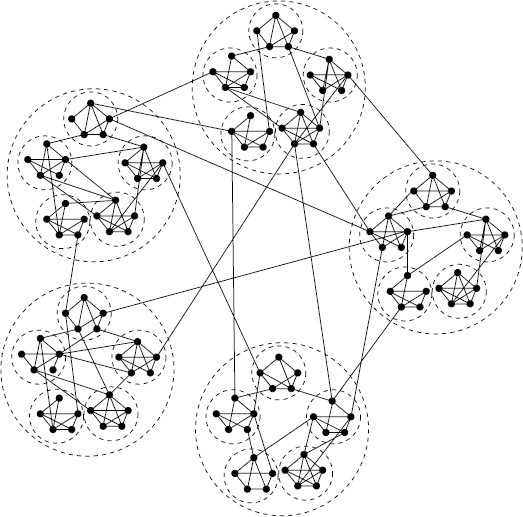
그리고 실제 네트워크는 뭉침현상(clustering)이 존재한다. 무슨 얘기이냐 하면, 특정 노트들끼리 뭉쳐있을 수 가 있다는 (cluster를 형성한다는) 의미이다. 따라서 밀그럼의 편지 실험에서 아무에게나 마구잡이로 편지를 전달하게 된다면 성공할 확률이 극히 낮아질 수 있다. (내부 cluster안에서만 편지가 빙빙 돌다가 실험이 끝날 수 있다.) 따라서 목표 지점과 현재 위치라는 굉장히 제한된 정보를 가지고 편지를 전달하기 위한 전략이 필요하고, 이를 다시 문제로 바꾸어서 생각해보면, 국지적인 정보만을 가지고 네트워크의 특정 지점에서 다른 특정 지점을 연결하는 가장 짧은 경로를 찾는 social search algorithm을 구현하기 위해서는 단순히 random하게 정보를 전달하는 것이 아니라, 어떤 특정한 rule이 필요하다는 것이다. 몇 가지 아이디어가 있는데, 대표적인 아이디어 중 하나는 사람들끼리의 연결은 그 정도가 같지 않다는 것이다. 즉, 내가 최종적으로 편지를 전달해야하는 사람이 은행가이므로 내 친구 중에서 간호사와 주식거래인이 있을 때 간호사보다는 주식거래인이 은행가와 확률적으로 사회적 거리가 더 짧을 것이라고 예측할 수 있을 것이다. 이런 식으로 특정 rule을 가지고 search를 하는 것이 매우 중요하다.

Small world & Network Modeling

자, 이제 중요한 개념 몇 개를 다시 정리해보자.

• Social Distance: Social Network에서 특정 node에서 다른 특정 node로 가기 위해 이동해야하는 가장 짧은 경로의 총 거리
• Clustering coefficient: Social Netwrok에서 특정 node들끼리 얼마나 cluster를 형성할 것인지를 결정하는 계수. 이 값이 클 수록 cluster를 더 많이 형성한다. 수학적으로 다시 정의하자면 Network에서 node들의 connection이 connected triple을 일고 있을 확률을 의미한다. 아래 그림을 참고하면 더 이해가 쉬울 것이다.
• 
• Diameter: Social Network에서 가장 긴 Social Distance의 길이
• Length of Network(L): 모든 social distance의 중간값. 일반적으로 그래프의 크기가 커지면 같이 커진다
• Small World: Network의 크기가 증가하는 속도보다 L이 증가하는 속도가 더 느린 형태의 네트워크 (보통 증가비율이 Logarithm scale이면 small network라고 한다.)

위의 용어들을 다시 명시한 채로 (몇 개는 새로 정의하였다) Real network를 생각해보자. 이전 실험들을 통해서 우리는 real network의 diameter는 매우 작은 편이라는 것을 알고 있고, 또한 clustering coefficient는 크다는 것을 알 수 있다. 그리고 중요한 컨셉 중 하나가 모든 social distance의 중간값인 L인데, 실제 네트워크에서는 그 네트워크의 크기가 커지는 속도보다 L이 더 천천히 증가한다. 이를 위에서도 언급했듯 Small World라고 한다.

근데 문제는 이런 Small world를 (한국어로는 좁은 세상이라고 한다) 수학적으로 모델링하는 것이 쉽지 않다. Power-Law 분포를 가진 네트워크를 앞에서 설명헀었는데, 이 모델을 (푸아송 모델이라고 한다) 적용해서 문제를 바라보게 되면 거리 혹은 지름이 짧다는 점에서 사실적지만, 모든 node가 independent possibility로 연결되어 있어서 뭉침계수가 작다는 점에서는 사실적이지 않다. 다시 뭉침계수를 설명하자면, 이어진 세 마디가 삼각형을 이루고 있을 확률이 뭉침계수이다. 그렇다면 Regular Network는 어떨까? 이 경우는 Clustering coefficient는 크지만 Diameter 역시 크다는 점에서 unrealistic하다. (이를 보완하기 위해서 그 둘을 적절하게 섞은 The Watts-Strogatz-Newman Model이라는 것이 있다. 이에 대해서는 아래에서 자세히 설명하도록 하겠다.)

Poisson Network vs Regular Network

푸아송 네트워크는 각 마디가 power-law distribution을 가지는 p라는 independent possibility로 연결이 되어있는 형태이다. random한 연결이 많기 때문에 diameter가 많다는 것은 충분히 이해할 수 있을 것이다. 그러나 이 경우에는 모든 마디가 p의 확률로 연결이 되기 떄문에, 엄청나게 약한 연결도 ‘연결’이 되기 때문에 cluster coefficient가 $C=p$로 작아서 사실적인 네트워크 모델이 될 수 없다. 반면 정규 네트워크는 네트워크 자체가 원형으로 구성되며 자기 자신과 가까운 c명에게 연결하고 있는 형태이다. 이 경우 cluster coefficient는 $C=\frac {3(c-2)} {4(c-1)}$로 크지만 (c의 값이 2명 값이 0이고 4면 0.5, 무한대로 가면 0.75가 된다. 이 정도면 엄청나게 높은거다.) diameter가 크기 때문에 사실적인 모형이 아니다. 때문에 이 둘을 적절히 결합한 The Watts-Strogatz-Newman Model이라는 것이 등장하게 되는데, 제일 가까운 c명과 연결이 되어있으면서 (regular network의 성질, 이로 인해 높은 clustering coefficient를 가지는 것이 가능하다.) 또한 특정한 independent possibility p로 random한 node와 link를 가지고 있다. (poisson network의 성질, 이로 인해 낮은 diameter를 가지는 것이 가능하다.) 이 모델은 얼마나 random하게 link를 형성하느냐에 따라 그 네트워크의 topology나, 성질 등이 달라지게 될 것이다. (아래 그림을 보면 이해가 될 것이다.)

아래 그림은 scholarpedia에서 가져온 그림이다. p가 0이면 정규 네트워크처럼 diameter와 clustering coefficient가 모두 높지만, p를 증가시키면 점점 Poisson network와 비슷해지는 것을 알 수 있다. 따라서 적절한 p를 고르는 것이 small world를 모델링하기 위해 매우 중요하다고 할 수 있다.

<h3 id=”34-4-socialsearch”>Fining paths - social search</h3>

그러면 이제 다시 local information만을 가지고 global shortest path를 찾는 문제로 돌아가서 생각해보자. 사실 이 문제는 optimization 문제로 치환해서 생각이 가능하지만, 안타깝게도 convex model이 아니기 떄문에 마냥 쉽게 적용하기는 쉽지 않다. 아무튼 다시 본론으로 돌아서, 가장 쉽게 생각할 수 있는 알고리듬은 greedy search algorithm이다. 내 neighbor 중에서 목표 node와 가장 가까울 것으로 생각되는 node로 넘어가고, 그 node에서도 마찬가지 과정을 반복하는 것이다. 하지만 당연한 얘기지만 이 알고리듬은 완벽하지 않다. 쉽게 생각해서, 내가 은행가와 가장 가까울 것이라고 예측한 주식거래인은 그 은행가를 직접적으로 모르지만, 간호사가 알고보니 그 은행가와 고등학교 동문이라 바로 연결이 되는 상황이라면? 이런 경우는 greedy algorithm이 global optima를 보장할 수 없게되는 것이다.

search algorithm을 위해 도임되는 모델 중에서 클라인버그(Kleinberg) 검색 모델이라는 것도 있다. 이 모형은 국지적으로 connection을 가지고 있고 거리 r에 따라 멀리 있는 사람과 $C * r^{-a}$의 확률로 connection을 가지고 있다고 가정한다. 이 모델에 따르면 $a = 2$ 일 때만 빠른 전달이 가능한데 그 모델링을 통해 예측한 결과는 아래 그래프와 같다.

그 이외에도 사람 사이의 관계를 tree로 정의하고 social ditance를 tree에서 거쳐야 하는 단계 수로 정의하는 Watts-Dodds-Newman Model이라는 것도 존재한다. 이 모델의 Social distance를 정의하는 두 사람이 서로를 알 확률 $p_m$은 $p_m = K 2^{\alpha m}$ 로 정의가 된다. 이 모델에서 level의 길이는 $log_2 \frac n g$로 정의가 되고, 평균적인 최단 거리도 계산이 가능하지만, 식이 꽤 복잡하기도 하고 이 모델의 reference도 찾지 못해 이 포스트에서는 생략을 하도록 하겠다 (직관적인 값이 아니라 이해를 위해 래퍼를 찾아봤는데 나오지 않는다) 아무튼 이 모델의 평균적인 최단거리에 node의 개수가 g이고 전체 사람이 n, a = 1이라는 특수한 경우로 문제를 바꾸어 생각해보면 평균 최단거리는 $log^2 ( \frac n g )$ 에 비례한다. 특이점이라면, 이 모델은 tree 구조로 생각을 했기 때문에 Hub의 존재는 고려가 되지 않는다는 점이다.

Conclusion

degree와 clustering을 동시에 만족하는 Network model은 현재까지는 없기 때문에 높은 clustering을 가지는 random distribution을 만드는 것도 활발한 연구 주제 중 하나라고 한다. 아무튼 network search의 핵심은 단순히 국지적인 정보만을 가지고 있어도 모든 Network에 정보 전파가 가능하다는 것이다. 아직도 연구가 활발히 진행되고 있는 분야이고, 정답도 없는 분야인 만큼 더 공부가 필요한 부분이라고 생각이 들었다. 이 포스트가 잘 이해가 되지 않거나 네트워크라는 것에 대해 흥미가 생긴다면 Linked: The New Science of Networks (Albert-laszlo Barabasi, Jennifer Frangos) 를 참고하면 될 것 같다.

+ 추가로 정송 교수님의 comment를 추가하고 글을 마무리 짓도록 하겠다.

Network search algoritm을 주변 resource를 검색하는 것으로 해석할 수 있을 것 같다. (ex 동물들의 먹이 탐색활동) genetic algorithm.. 현재 search space 내에서 solution에 대한 initial guess를 가지고 solution을 가지고 찾다가 간헐적으로 mutation이 일어나 다른 candidate space에서 solution을 찾는 모델이 있음. 지금 network search에 대한 설명을 들어보니 그와 비슷한 것 같다. 클라인버그 검색 모형에서도 a에 따라 a 세팅을 잘못하면 국지적으로 값을 찾을 수 없거나 혹은 너무 mutation이 자주 일어나서 잦은 swing현상으로 인해 최적화가 안된다.

Modern network에 P2P같은 형태가 존재한다. 움직임에 의한 연결. 둘이 움직이다가 연결이 일어난다고 생각해보자. 만약 네브라스카가 움직이지 않는 static한 network라면 그 contact이 없지만, 만약 그 사람 중 하나가 mobility를 가지고 예를 들어 여행을 많이 다니는 사람이 하나 있어서 그 connection이 많이 일어나는 사람이 있다면 그 사람이 Network의 key가 되며 이것에 대한 수학적 모델링을 통한 연구가 이뤄지고 있다.