README   SanghyukChun's Blog

Machine Learning 스터디 (5) Decision Theory

| Comments

들어가며

그 어떤 좋은 알고리즘을 선택하더라도, 최종적으로 특정 문제에 대해 inference를 하기 위해서는 decision making을 해야만 한다. 그렇다면 decision은 어떻게 내릴 수 있을까? 라는 질문이 자연스럽게 들 수 있는데, decision theory는 어떻게 decision을 내릴지에 대해 다룬다. 내가 지금 결정한 parameter는 적당한 parameter인가? 예를 들어서 내가 임의의 데이터를 가장 잘 설명할 수 있는 1차함수를 그려야하는 상황이라고 했을 때, 나는 그 ‘가장 잘 설명할 수 있는’ parameter를 어떻게 decide할 수 있을까, 어떻게 decision making을 할 수 있을까. 혹은 Classification problem에서 해당 data가 어떤 class에 속하는지 어떤 방식으로 decision을 내려야할까?

Decision rule with prior only

다시 Bayes Rule로 돌아가보자.

$$ p(C|X) = {p(X|C) p(C) \over p(X)} $$

이전 글에서 prior라는 것에 대해 언급했었다. 예를 들어 우리가 어떤 classification을 하는 상황이라 해보자. 만약 주어진 데이터가 class A인지 B인지 구분해야하는 상황이라고 가정을 해보자. 우리가 아는건 prior P(C) 밖에 모르는 상황이라고 해보자. 그렇다면 우리가 내릴 수 있는 가장 합리적인 판단은 무엇일까? 이 상황에서의 가정은 우리가 아는 정보는 오직 prior밖에 없으며, incorrect classification에 대한 cost는 모두 동일하다고 가정한다. 그렇다면 당연히 reasonable한 decision rule은 가장 높은 확률을 가지는 class를 선택하는 것일 것이다. 이유는 가장 확률이 높은 클래스를 C1이라 하면, 언제나 $P(C1) > P(C2)$ 라는 사실을 알 수 있기 때문이다. 즉, 언제나 C1을 고르는 것이 가장 best하다. 그렇다면 여기에서 문제가 발생하는데, 만약 우리가 모든 decision을 동일하게 내리게 된다면 당연히 좋은 결과가 나올리가 없다는 점이다. 예를 들어 C1이 60%, C2가 40% 존재하는 상황이면, 언제나 error는 0.4가 될 것이며, 언제나 classification result는 C1이 될 것이기 때문이다. 그러나 일단 우리가 prior만 가지고 있다고 가정하고 있기 때문에 이런 상황에서는 언제나 이것이 best가 될 것이다. 그렇다면 이 이외의 다른 정보를 가지고 있다면 어떨까?

Decision rule with Likelihood

Observation, 혹은 Likelihood에 대한 정보를 가지고 있다면 분명 상황은 더 나아질 수 있다. 확률로 표시하자면 이 값은 $P(X|C)$, 즉 주어진 클래스에 대해 관측되는 데이터가 된다. 그리고 당연하게도, 우리가 이 값을 가지고 있다면, Bayes rule에서부터 P(C|X), 혹은 posterior를 계산할 수 있게 된다. 즉, prior와 likelihood를 알고 있으므로, $C = argmax P(C|X) = argmax {P(X|C) P(C) \over \sum_i P(X|C_i) P(C_i) } $ 를 통해 decision을 내릴 수 있게 된다. 그렇다면 이렇게 선택하는 경우 error는 어떻게 나타나게 될까? 여기에서 error는 classification이 틀린 경우를 의미한다 (number of misclassification). 일단 class가 2개 밖에 없다고 해보자. 그럼 error가 발생하는 경우는 단 두가지인데,

$$P(error|x) = \begin{cases} P(C1|X) \text{ if we decide C2} \\ P(C2|X) \text{ if we decide C1} \end{cases} $$

이렇게 두 가지가 될 것이다. 즉, 우리가 P(C|X)를 maximize하는 C를 선택하는 decision rule을 가지고 있다면, P(error)는 간단하게 다음과 같이 계산된다

$$P(error) = \int P(error|X) P(X) dX $$

가 될 것이며, 이 결과를 최소화하는 decision making rule이 우리가 원하는 decision rule이 될 것이다. (당연히 우리는 결과의 error가 최소화되는 것을 원할테니까.) 결론만 놓고 얘기하자면 prior와 likelihood를 모두 알고 있다면 위와 같이 posterior를 maximize하는 것이 가장 이 값을 $P(error|X) = min[P(C_1|X), …, P(C_k|X)]$ 로 최소화 시킬 수 있다. (이유는 조금 생각해보면 간단하게 알 수 있다.) 즉, 모든 class의 posterior를 계산하여 주어진 데이터에 대해 얻어질 확률이 가장 큰 class를 선택하는 것과 정확히 같다는 의미이다. (참고로 만약 prior에 대한 정보가 없어서 uniform한 prior를 가정하게 된다면 결국 likelihood만을 놓고 계산한 값과 정확히 일치하게 된다.)

Loss function

앞서 설명한 예제는 “misclassification number”를 minimize하는 예제였다. 그러나 실제 많은 application들에서 이런 방식 이외의 다른 approach를 요구하게 된다. 예를 들어서 값이 틀렸을 때 0과 1로 error를 정의하는 것이 아니라, 원래 target data와 우리가 계산한 estimated data의 차이의 제곱의 합들로 표현을 할 수도 있고, 제곱이 아니라 절대값의 합으로 표현할 수도 있다. 즉, 보다 더 generalized된 접근법이 필요한데, 가장 formal하게 많이 쓰이는 decision criteria 중 하나로 loss function 혹은 cost function이 있다. Cost function은 여러가지로 정의할 수 있겠지만, 나는 Cost function을 이렇게 정의한다. 우리가 목표로 하는 가장 좋은 결과와 지금 내가 선택한 결과와의 차이. 즉, 내 결과가 optimal한 결과보다 좋지 않으면 않을수록 cost function은 커지고, 당연히 optimal한 결과를 가지게 됐을 때 Cost function의 값이 가장 작아질 것이다. 다만, 그 차이는 여러가지 방법으로 정의할 수 있는데, 앞서 misclassification number와 같은 binary한 차이가 될 수도 있고, 또 앞서 내가 예로 들었던 원래 값과 예상 값의 차이의 제곱의 합.. 등 굉장히 다양하게 cost function을 정의하는 것이 가능하다. 그리고 이런 함수는 true value가 변하지 않고, parameter에 따라 estimated value가 변하게 되므로, loss function은 parameter에 대한 함수로 나타나게 된다. 이때, Loss function은 $L(\theta, \hat \theta(X))$로 표기되며, 우리가 찾고자하는 true parameter를 $\theta$, 주어진 data X에 대해 estimate한 parameter를 $\hat \theta(X)$라 하자. 우리의 목표는 가장 적절한 parameter $\hat \theta(X)$를 찾는 것이다.

Minimize Bayes Risk

자 다시 Decision rule로 돌아가보자. 우리가 minimize하고 싶은 것은 Loss function을 minimize하는 것이지만, 그 값 자체가 true value에 dependent하기 때문에 정확한 값을 구하는 것이 불가능하다. 따라서 주어진 데이터 X에 대해 expectation을 계산하여 이를 해결하게 된다. 주어진 데이터들에 대한 loss function의 expectation은 $R = \int \int L (\theta, \hat \theta(x)) p(\theta, x) dx d \theta $ 로 표현이 되는데, 이 값은 사실 posterior의 risk, 혹은 conditional risk라고 알려진 $R = \int L (\theta, \hat \theta(x)) p(\theta | x) d \theta $ 값을 minimize하는 것과 일치한다. Expected Loss, 혹은 Bayes risk를 전개해보면

$$R = \int \int L (\theta, \hat \theta(x)) p(\theta, x) dx d \theta \\ = \int \int L (\theta, \hat \theta(x)) p(\theta | x) p(x) dx d \theta \\ = \int \left( \int L (\theta, \hat \theta(x)) p(\theta | x) d \theta \right) p(x)dx $$

이때, $\theta$에 대한 적분 구간이 정확하게 conditional risk와 같으며, x에 대해 summation하는 것은 parameter에 영향을 주지 않으므로 둘이 동일함을 알 수 있다. 이렇게 구해진 expectation loss, Bayes risk (혹은 이와 같은 posterior risk, conditional risk) 를 minimization시키는 방법으로 $\hat \theta$를 estimate하는 estimator를 Bayes estimator라고 한다.

그러면 다양한 loss function들에 대해 이 Bayes risk와 Bayes estimator로 얻어지는 parameter를 계산해보자.

간단한 예로 zero-one loss의 expected loss를 구해보자. Zero-one loss는 아래와 같이 주어진다. 이 경우는 class를 구하는 것이므로 $\theta$가 아니라 $C_k$로 작성하였다.

$$L(C_k, \hat C_k(x)) = \begin{cases} 1 \text{ if } C_k = \hat C_k(x) \\ 0 \text{ otherwise } \end{cases} $$

따라서 expectation loss 혹은 그와 동일한 conditional risk $R = \sum_j L (C_j, \hat C_j(x) p(C_j | x) $ 는 (이 경우는 discrete하므로 integral이 아니라 summation이다.)

$$R = \sum_j L (C_j, \hat C_j(x) p(C_j | x) = \sum_{j \neq i} P(C_j | X) = 1-P(C_i|X) $$

와 같이 얻어지게 된다. 따라서 zero-one loss를 decision rule로 삼게 되면 아래와 같은 결과를 얻게 된다.

$$C_i = argmin R = argmin_{C_k} 1 - P(C_k|X) = argmax_{C_k} P(C_k|X) $$

즉, 0-1 loss를 사용하게 되면 Bayes estimator가 MAP (maximum a posterior)와 같아진다는 사실을 알 수 있다.

이번에는 다른 Loss function을 사용해서 bayes risk를 계산해보자. 만약 우리가 $L (\theta, \hat \theta(x)) = (\theta - \hat \theta)^2 $ 이라 한다면 어떻게 될까. 먼저 conditional risk는 아래와 같다.

$$R = \int (\theta - \hat \theta)^2 p(\theta | x) d \theta p(x) $$

위의 식을 $\hat \theta$에 대해 미분해보면,

$$ \frac{\partial}{\partial \hat \theta} \left[ \int (\theta - \hat \theta)^2 ) p(\theta | x) d\theta \right] \\ = \int \frac{\partial}{\partial \hat \theta} \left[ (\theta - \hat \theta)^2 ) p(\theta | x) d\theta \right] \\ = -2 \int (\theta - \hat \theta) ) p(\theta | x) d\theta$$

이 derivation을 0으로 만드는 $\hat \theta$는 간단하게 $\hat \theta = \int \theta p(\theta | x) d \theta = E[\theta|x]$라는 결과를 얻게 된다. 즉, Bayes risk를 가장 minimize하는 $\hat \theta$는 주어진 데이터에 대한 parameter의 expectation인 $E[\theta|x]$라는 사실을 알 수 있다. 그리고 이를 다시 conditional risk에 대입을 해보면

$$R = \int (\theta - E[\theta|x]^2 p(\theta|x) d\theta = \sigma^2_{\theta|x}$$

즉, risk가 random variable의 variance와 정확히 같다는 것을 알 수 있다. 또한 따라서 Bayes risk가 절대로 0으로 수렴하지 않음도 알 수 있는데, 우리가 구한 결과에 따르면 이 값은 항상 $\theta|x$라는 random variable의 variance와 같기 때문에 이 값이 0이라는 얘기는 더 이상 $\theta|x$가 random variable이 아니라 deterministic하다는 의미가 되기 때문이다. 따라서 이 값은 항상 0이 아님을 알 수 있다.

Inference and decision

다시 Classification problem으로 돌아가보자. 이 classification은 크게 두 가지 step으로 나눌 수 가 있는데 하나가 inference stage이고, 또 하나가 decision stage이다. Inference stage에서는 training data를 사용하여 $p(C_k|x)$를 계산하기 위한 model을 learning한다. 그리고 그에 따르는 다음 step인 decision stage에서는 앞서 inference stage에서 계산한 posterior probability를 사용하여 실제 class assignment decision을 내리게 된다. 이런 과정 없이 단순하게 input x에 directly decision을 mapping하는 function을 생각할 수도 있는데, 이런 function은 discriminant function이라 한다.

이런 inference와 decision stage로 classification을 구분하는 approach를 취하게 되면 크게 두 가지 방법으로 decision problem을 접근하는 것이 가능해진다. Generative model과 Discriminative model이 바로 그것이다.

Generative model은 input에서부터 distribution을 직접적으로 혹은 간접적으로 얻어내고 output 역시 마찬가지 방법으로 얻어내게 된다. 조금 더 구체적으로 들어가보자. Generative model은 가장 먼저 inference problem, 정확히는 각각의 class 별로 가지게 되는 class conditional density $p(x|C_k)$를 결정하는 inference prblem을 풀게 된다. 또한 class prior probability $p(C_k)$도 infer를 하게 된다. 이 두 가지 정보를 사용하여 Bayes rule을 적용하여 posterior probability $p(C_k|x)$를 계산하게 된다.

$$ p(C_k|x) = {p(x|C_k) p(C_k) \over p(x)} $$

이때, $p(x)$는 단순히 normalize를 해주는 것으로 무시할 수 있다. (자세한건 이전 글에서 설명했으므로 생략.) 따라서 우리가 assume해야하는 값은 $p(x|C_k)$, 그리고 $p(C_k)$인데, 결국 이 둘을 assume하는 것은 $p(C_k, x)$를 assume하는 것, 혹은 modeling하는 것과 같다. 즉, generative model은 joint probability를 modeling 하여 sample들을 해당 distribution으로 ‘generate’ 한 결과를 사용하여 decision을 내리는 것이다.

이런 Generative model의 예로는 Gaussian Mixture Model (GMM), Hidden Markov Model (HMM), Naïve Bayes, Restricted Boltzmann Machine (RBM) 등이 존재한다.

이에 반해 Discriminative model 은 inference problem에서 posterior class probability $p(C_k|x)$를 직접 계산한다. 그리고 decision stage에서 이 posterior probability를 직접 사용하여 decision을 내리게 된다. 즉, 새로 들어온 input x에 대해 모든 class들의 posterior를 계산하여 가장 probability가 높은 class를 assign하는 방식으로 classification을 하게 된다. 위애서 길게 설명했던 Generative model과의 가장 큰 차이는 Generative model은 joint distribution $p(x, C_k)$를 계산하여 inference와 decision을 하는데에 반해 Discriminative model은 그것을 직접 계산하여 inference를 한다는 점이 다르다.

Discriminative model의 예는 Logistic regression, Linear discriminant analysis (LDA), Support Vector Machines (SVM), Boosting, Conditional Random Fields (CRF), Linear Regression, Neural Networks 등이 존재한다.

Generative model 과 Discriminative model의 차이점은 아래 그림에서 간단하게 정리되어있다. (출처)

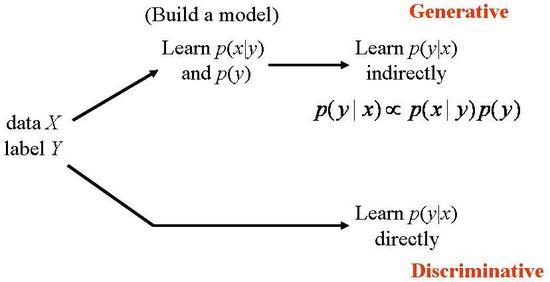
즉 데이터 x와 그 데이터들의 class y가 주어졌을 때, Classification을 위해서 필요한 값은 결국 $p(y|x)$로 같지만, generative model은 먼저 $p(x|y), p(y)$를 modeling하고 이 값들을 learning한 이후에 $p(y|x) \propto p(x|y) p(y)$를 통해 데이터 x의 class y의 확률을 계산하게 된다. 반면 discriminative model은 model 자체가 $p(y|x)$를 바로 learning하기 때문에 이 값을 바로 사용하면 된다. 따라서 discriminative model은 어떤 식으로 class가 분포해 있는지 사전 정보를 알 필요가 전혀 없지만, generative model을 사용하기 위해서는 이 값을 내가 미리 assume해야만 한다. 간단하게 생각하면 SVM은 대표적인 discriminative model 중 하나인데, SVM의 그 어떤 과정도 주어진 class들이 특정 형태로 분포해야한다는 가정이 전혀 들어있지 않다. 반면 generative model 중 하나인 GMM은 모든 cluster들이, 혹은 class들이 Gaussian의 mixture 형태로 주어진다고 가정하게 된다. 즉, 이 경우는 데이터와 class의 joint probability를 계산하게 되는 것이다.

정리해보면 Generative model은 joint distribution에서부터 sample을 ‘generative’하는 반면, Discriminative model은 주어진 데이터 x에 대해서만 model을 구하게 된다. 따라서 일반적으로 generative model이 훨씬 더 flexible한 결과를 보인다. 그러나 joint distribution을 직접 계산하는 것은 매우 computation cost가 높은, 즉 complexity가 높은 작업인 경우가 대다수인 반면, posterior probability를 계산하는 것은 상대적으로 더 저렴한 경우가 많다. 그 뿐 아니라, joint distribution을 modeling 하는 것도 대부분 쉽지 않다. 주어진 데이터들이 어떤 joint distribution으로 분포했는지는 modeling을 하지 않고서는 알 수 없기 때문이다. 반면 $p(y|x)$는 우리가 관측하는 likelihood 등을 사용하여 바로 계산하는 것이 가능하기 때문에 대부분의 discriminant model은 아무래도 조금 더 데이터가 sparse하게 존재하는 경우라거나, 전체 우리가 그 joint distribution에 대해 감조차 잡을 수 없는 경우에 해야하는 classification에 적합한 결과를 내놓는 경우가 많다고 한다.

Decision process

정리하자면, 최종적으로 decision을 내리기 위해서는 (1) Find parameter by minimizing risk (2) Decision by Model 이라는 과정을 거치게 된다. 먼저 minimize risk는 위에서 서술한 bayes risk를 minimization하는 부분으로, 이 부분에서 우리는 parameter들을 learning하게 된다. 이때 Loss function을 어떻게 정의하냐에 따라 parameter의 값이 결정되게 되며, 나중에 다루겠지만, 단순히 loss function을 정의하는 것으로 끝나는 것이 아니라, 이 optimization 문제를 polynomial algorithm을 통해 계산해내어야한다. 실제로 많은 algorithm들이 global optimum으로 수렴하지 않고 local optimum만을 찾아주는 경우가 많다. 이렇게 parameter를 learning한 이후에는 parameter를 사용해 posterior를 계산하게 된다. 이때 Model에 따라 inference를 하는 방법이 달라지게 되는데 discriminative model은 parameter를 사용해 directly하게 posterior를 계산하게 되고, generative model은 joint distribution을 learning하여 posterior를 indirectly하게 유추하게 된다.

변경 이력

  • 2014년 8월 19일: 글 등록
  • 2015년 2월 28일: 변경 이력 추가

Machine Learning 스터디의 다른 글들