README   SanghyukChun's Blog

Machine Learning 스터디 (10) PAC Learning & Statistical Learning Theory

| Comments

들어가며

어떤 머신러닝 모델이 있을 때 이 모델이 다른 모델에 비해 뛰어나다고 주장하려면 어떤 것들이 필요할까? 알고리즘은 수렴성이나 complexity 등으로 성능을 논하지만, 모델의 성능을 표현하기 위해서는 다른 무언가가 필요하다. 이번 글에서는 PAC (Probably Approximately Correct) 라는 개념을 설명할 것이다. PAC는 이론적으로 모델의 성능을 측정하는 방법 중 하나로, 비록 practical하게 모델의 성능 측정에 쓰기는 힘들지만 개념적으로 왜 특정 모델이 더 좋은지, 언제 모델의 성능이 좋고 언제 나쁜지에 대해 설명하는 것은 가능하다. 이 글에서는 Computational learning theory 라는 분야를 언급하고, 그 다음 PAC의 기본 개념과 그 intuition을 설명할 것이다. 그리고 VC dimension을 소개하여 일반적인 infinite hypothesis space에서 PAC bound를 어떻게 다시 bound 시킬 수 있는지 등에 대해 설명할 것이다.

Motivation

다시 원래 질문으로 되돌아가서 모델이 ‘뛰어나다’ 라고 말하기 위해서는 어떤 요소들이 필요할지 생각해보자. 먼저 다른 모델에 비해 learning하는 데에 필요한 데이터의 수가 적어야할 것이고, learning한 이후에 inference를 했을 때 그 결과가 좋아야할 것이고, 마지막으로 learning이 가능한 상황이 많이 있어야한다. 예를 들어서 어떤 모델을 만들었는데, 이 모델이 너무 복잡해서 100번 learning시켰을 때 (overfitting등의 이슈로 인해) 오직 3번 정도만 제대로 learning이 된다고 하면 이 모델은 쓸모없는 모델일 것이다. 따라서 ‘좋은 모델’ 인지 여부를 판단하기 위해서는 다음과 같은 질문들에 대답을 해야한다.

  • “Seccessful” learning을 할 확률
  • Learning에 필요한 training example의 개수
  • ML algorithm에 의해 구해진 approximated target function의 정확도

이런 질문들에 답을 하기 위해 등장하게 된 분야가 바로 Computational learning theory으로, machine learning algorithm의 분석을 위한 수학적이고 이론적인 분야라고 생각하면 될 것 같다. 오늘 다루게 될 PAC는 이 computational learning theory의 한 부분으로, 가장 간단한 이론 중 하나이지만, 그 만큼 이론적으로 시사하는 바가 많은 이론이기 때문에 많은 machine learning course에서 한 번은 언급하고 넘어가는 경우가 많다.

Revisit: Machine Learning in function approximation view

맨 처음 글에서 설명했던 Machine learning의 구성요소에 대해 다시 살펴보도록 하자. 이 글에서는 machine learning의 역할이 특정 데이터의 결과를 예측하는 function을 찾는 것이라고 가정할 것이며, 따라서 error는 함수 값이 정확하게 찾아진 데이터의 수와, 그렇지 않은 수에 의해 0에서 1사이의 값으로 정확하게 정의된다. 이때 Machine learning은 다음 요소들로 구성된다.

  • Instance $X$: 모든 데이터의 공간이라 할 수 있다. 즉, 모든 픽셀이 0 또는 1인 28 by 28 흑백 이미지라고 한다면 $2^{784}$ 크기의 set이 될 것이다.
  • Target concept $c$: 혹은 우리에게 조금 더 익숙한 용어로 표현하면 ‘target function’이다. Instance space의 subset으로 정의가 되며, 주어진 데이터가 어떤 값을 가지는지 판단하는 함수라고 생각하면 된다. 예를 들어 MNIST classification 문제에서는 주어진 데이터 x가 [0-9] 사이의 데이터 중에서 어디에 속하는지 판단하는 함수가 될 것이다.
  • Hypothesis space $H$: 주어진 $c$와 최대한 비슷한 approximated function (hypothesis) $h$가 속하는 function space이다. 예를 들어 함수가 linear라 가정한다면 Hypothesis space는 모든 linear function의 function space가 된다.
  • Training Data $D$: 모든 instance space를 다 볼수는 없으니 그 중 일부의 데이터만이 training data로 주어진다.

위의 4가지 요소가 주어졌을 때, Machine learning 모델은 전체 데이터셋 $x \in X$ 에 대해 가장 target concept $c(x)$와 비슷한 hypothesis $h(x)$를 찾아야한다. 하지만 실제로는 training sample $x \in D$ 만 관측할 수 있으므로, training error 관점에서 hypothesis를 찾아야한다. 여기에서 중요한 점은 전체 instance $X$의 subset인 training instance $D$에서 error가 minimize가 된 모델이, 전체 instance에 대해서도 역시 작은 error를 보일 것인지, 만약 그렇지 않다면 training error와 true error가 얼마나 차이날 것인가 하는 점이다. 이 둘의 관계는 아래와 같은 그림으로 이해할 수 있다.

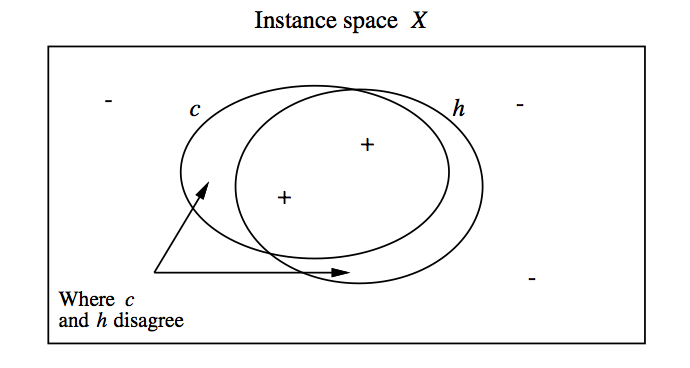
위의 그림에서 $h$와 $c$가 정확히 겹쳐지지 않는 것을 볼 수 있다. 여기에서 ‘There is no free lunch’ 라는 머신러닝의 큰 교훈이 나온다. 만약 우리가 어떤 모델을 training data에서 관측하지 못한 데이터에 대해서도 더 generalize하고 싶다면 모델에 대한 더 많은 assumption이 필요하다는 의미이다. 이 assumption은 흔히 regularization으로 표현되기도 한다. Multi-layered perceptron 모델에서 dropout이나 batch normalization, l2-regularization 등과 같은 더 많은 assumption이 있어야 더 generalized된 모델을 얻을 수 있다는 것이다.

여기에서 한 가지 또 중요한 점이 있는데, 심지어 데이터에 noise가 전혀 없어서 우리가 항상 정확한 target value를 알 수 있다고 하더라도, true error와 train error의 차이는 언제나 발생할 수 있다는 것이다. 이해를 돕기 위하여 예를 들어보자. 만약 아래와 같은 데이터가 있어서, 박스 R의 안 쪽은 +, 바깥쪽은 -인 target value를 가진다고 가정해보자. 전체 도메인에서 우리는 uniformly sample된 데이터들의 target value만을 알고 있다고 가정하자. 이 상황에서, 우리가 이 경계 R이 box라는 것을 알고 있을뿐아니라, error가 전혀 없는 데이터를 가지고 있다고 하더라도, R과 “정확하게 같은” 경계를 얻는 것은 거의 불가능하다는 사실을 알 수 있다.

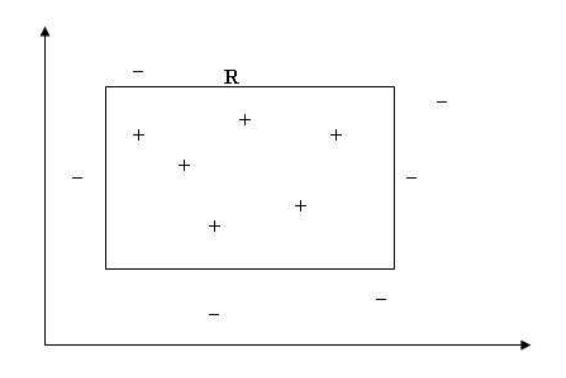
물론 엄청나게 많은 데이터가 있으면 “거의 같은” 경계를 얻을 수는 있겠지만, “정확하게 같은” 경계를 얻는 것은 역시 거의 불가능하다. 따라서 우리는 “정확한” 모델을 얻기위해 얼마나 많은 데이터가 필요한가? 라는 질문이 아니라 “이 정도의 아주 작은 error를 높은 확률로 달성하기 위해 어느 정도의 데이터가 필요할까?” 정도로 질문을 바꿔야한다.

Overfitting: revisited

이제 true error와 train error를 정의해보자. 이 둘은 각각 전체 데이터셋 $X$와 traning data set $D$에서의 learning된 hypothesis $h$의 error로 정의된다. 수식으로 표현하면 다음과 같다.

당연한 얘기지만, 우리가 모든 데이터를 관측할 수 없기 때문에 정확한 true error를 측정하는 것은 불가능하다. 그러나 만약 우리가 test data를 모든 데이터셋에서 uniformly random하게 (i.i.d하게) 뽑는다면 test error는 true error의 unbiased estimator가 된다. 이 글에서는 반드시 test data가 i.i.d하게 뽑혔다고 가정하고 test error를 true error의 unbiased estimation으로 취급할 것이다. 즉, 앞으로 test error라고 언급하는 것들은 전부 true error와 같다고 생각해도 된다.

그러나 test error와는 달리, training error는 true error의 unbiased estimator가 아니다. 왜냐하면 error가 hypothesis $h$에 의해 결정이 되는데, $h$는 다음과 같이 training data $D$에 dependent하기 때문이다.

위와 같이 train error를 minimize하는 것을 empirical risk minimization이라고 부르며, $h$는 항상 true error보다 training error가 더 좋을 것이라는 추측 역시 할 수 있다. 여기에서 우리는 overfitting이라는 것을 다음과 같이 정의할 수 있다.

Hypothesis $h \in H$는 다음과 같은 조건을 만족하는 $h^\prime \in H$가 존재할 때 train data에 overfitting 되었다고 정의한다.

여기에서 우리는 머신러닝의 또 한가지 큰 교훈인 “Occam’s razor”를 배울 수 있다. 먼저 아래 그림을 살펴보자. 이 그림은 decision tree의 size가 커지면 커질수록 (모델이 더 복잡해지면 복잡해질수록) training error는 감소하지만 true error는 오히려 증가한다는 것을 보여준다.

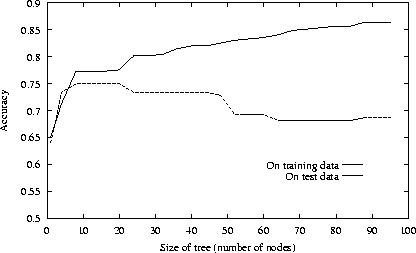
여기에서 우리는 model의 complexity가 커질수록 overfitting의 효과가 더 강력해진다는 것을 알 수 있으며, 이를 Occam’s razor라고 한다. 즉, 할 수 있으면 최대한 간단한 모델이 좋다는 것이다. 또 하나 흥미로운 점은, 만약 training data가 infinite하여 모든 data space를 포함할 경우 더 이상 overfitting 문제는 없을 것이라는 것이다. 그러나 실제로는 무한한 데이터를 전부 학습하는 것이 불가능하고 제한된 숫자의 데이터만을 사용해야하기 때문에 그런 일은 발생하지 않는다. 그 대신, 우리는 ‘얼마나 많은 데이터가 있어야 overfitting 이슈가 줄어들까?’ 라는 유의미한 질문을 할 수 있다.

PAC Learning: Introduction

PAC (Probably Approximately Correct) learning이란 수학적으로 머신러닝 모델을 분석하는 framework으로, “높은 확률로 (Probably)” 주어진 모델이 “작은 error를 가진다 (Approximatly Correct)”와 같은 식의 분석을 할 수 있다. 앞으로 진행하는 모든 설명과 증명에서 data에 noise가 없다고 가정하도록 하겠다. 앞에서도 보았듯, 데이터가 전혀 노이즈가 없다고 하더라도 정확하게 true error가 0이 되는 모델을 얻는 것은 거의 불가능하기 때문에 확률적으로, 그리고 error라는 관점에서 모델을 분석하게 되는 것이다.

PAC bound는 다음과 같은 4가지 요소들로 구성된다.

  • Training data의 샘플 수 $m$
  • Train error와 true error의 gap $\varepsilon$, $\mbox{error}_{true}(h) \leq \mbox{error}_{train}(h) + \varepsilon$
  • Hypothesis space의 complexity $| H |$, 만약 model parameter가 infinite하다면 다른 표현이 필요하다
  • Confidence of the relation: at least $(1-\delta)$

그리고 finite hypothesis space에 대해, PAC bound는 다음과 같이 주어진다.

수식에서 볼 수 있듯 PAC bound는 true error와 train error의 gap의 upper bound를 training data의 개수 $m$, model complexity $|H|$, 그리고 error와 그 confidence $\varepsilon$과 $\delta$에 대해 표현하는 bound이다. 이 bound에서부터 우리는 모델의 성능, 정확히 말하면 generalization과 overfitting에 대한 앞에서 살펴본 intuition을 다시 한 번 확인할 수 있다. 왜냐하면 true error와 train error의 gap $\varepsilon$이 generalization, 그리고 overfitting과 관련된 term이기 때문이다. Generalization은 그 정의 자체가 $\varepsilon$과 큰 차이가 없으니 넘어가고, 왜 overfitting과 관련된 term인지만 살펴보자. 앞에서 overfitting을 정의할 때, train error는 더 나쁘지만, true error는 더 좋은 대체 모델 $h^\prime$ 이 존재할 때 $h$가 train data에 overfit되었다 정의했는데, $\varepsilon$이 커지면 커질수록 그런 모델 $h^\prime$이 존재할 확률이 커지므로, $\varepsilon$은 overfitting과 관련된 term이 되는 것이다. 따라서 이로부터 우리는 다음과 같은 intuition들을 얻을 수 있다.

  • Training data의 개수가 많으면 많을수록 ($m$이 클수록) 모델은 더 generalize되고, overfitting의 위험성도 작아진다.
  • Model complexity가 높을수록 ($|H|$가 클수록) 모델 generalization은 더 어려워지고, overfitting의 위험성 역시 커진다.
  • Model의 성능을 끌어올리려면 (true error를 줄이려면) train error를 줄이거나, training sample을 늘리거나, 모델 complexity를 줄여야한다.

PAC Learning with Finite Hypothesis Space: Proof

이제 앞에서 살펴본 hypothesis space가 finite할 때 PAC bound를 증명해보자. 먼저 문제를 단순화하기 위해 $\mbox{error}_{train}(h) = 0$ 라고 가정하자. 이때 우리는 training error는 0이면서, true error는 $\varepsilon$ 보다 큰 hypothesis $h^\prime$가 존재할 확률이 다음과 같음을 보일 수 있다.

이 수식을 (A)라 하고 증명은 잠시 뒤로 넘기자. 이제 $|H| \exp(\varepsilon m) \leq \delta$를 만족하는 $\delta$를 하나 잡아보자. 이 간단한 수식에서부터 우리는 training sample의 개수와 true error의 upper bound를 $\varepsilon$, $|H|$, $\delta$, $m$에 대한 term으로 표현할 수 있다.

즉, 이 bound들을 통해서 모델이 복잡할수록, 그리고 error에 대한 upper bound가 작아질수록 더 많은 데이터가 필요하다는 사실을 알 수 있다. 만약 우리가 어떤 모델의 성능을 더 개선시키고 싶다고 했을 때 (true error를 더 줄이고 싶을 때), 위의 수식에서부터 training error를 줄이거나, training sample의 개수를 늘리거나, 더 간단한 모델을 고르는 등의 (Occam’s razer) action을 취해야한다는 것 역시 알 수 있다.

그러나 위의 intuition들은 전부 traininig error가 0일 때 얻은 값이기 때문에 training error가 0이 아닐 때에 대해서도 bound를 증명해야한다. 다행히 위에서 얻은 결과를 사용하면 traininig error가 0이 아닐 때도 Hoeffding bound를 통해 다음과 같은 bound를 얻는 것이 가능하다. (증명은 생략한다.)

그리고 위에서 얻은 두 개의 bound 역시 아래와 같이 새롭게 증명할 수 있다.

식의 모양은 살짝 바뀌었지만 근본적인 intuition은 그대로 유지된다.

PAC Learning with Finite Hypothesis Space: Proof of (A)

사실 앞 section에서 증명한 수식은 전부 다음 수식에서부터 시작한다. 이 section에서는 아래 수식을 증명해보겠다.

수식을 좀 더 간단하게 적기 위해 $\mbox{error}_{true}(h)$를 $err(h)$로 표현하도록 하자. 이제 Hypothesis $h^\prime$이 $err(h^\prime) > \varepsilon$라는 조건을 만족할 때, $h^\prime$이 ‘bad’하다고하고, bad hypothesis들의 set을 $B$라고 부르자. 모든 training sample에 대해 error가 0이고 ($h^\prime(x_i) = c(x_i) ~\forall x_i \in D$, $h^\prime$ is consistent with training samples), 모든 true sample들에 대해서는 $err(h^\prime) > \varepsilon$를 만족하는 hypothesis $h^\prime$이 존재한다고 가정해보자. 이때 $h^\prime$은 $B$에 속하는 element이고, 이런 hypothesis는 하나보다 더 많을 수 있기 때문에, 아래와 같은 수식을 유도할 수 있다.

이제 $B$는 $H$의 subset이므로 다음과 같은 수식을 유도할 수 있고, 증명이 끝이 난다.

PAC Leanring with Infinite Hypothesis Space

위에서 열심히 증명하기는 했으나, 이 bound는 사실 practical하게는 아무런 쓸모가 없는 bound이다. 왜냐하면 $|H|$가 finite한 어떤 값을 가진다고 가정했기 때문인데, 만약 $f(x | a, b) = ax + b$ 라는 함수만 주어지더라고 a와 b이 real number라면 $H$가 infinite set이 되기 때문에 bound가 의미가 없어진다. 이 때문에 새롭게 도입되는 개념이 VC (Vapnik–Chervonenkis) dimension이라는 개념이다.

VC dimension $VC(H)$는 hypothesis space $H$에 대해 정의되며, classification algorithm의 capacity를 측정하기 위해 사용되는 방법이며, Instance space $X$에 대해 Hypothesis space H의 VC(H)는 $H$로 shatter할 수 있는 가장 큰 $X$의 finite subset 크기와 같다. 이때 shatter란 labeling에 상관없이 정확하게 classify하는 것을 의미한다. 이 개념은 실제 예시를 통해 이해하는 것이 제일 빠르므로 몇 가지 예시들을 들어보도록 하자.

먼저 linear model은 $d$-dimensional space에서 VC dimension이 d + 1 이다. 자고로 이런건 말보다 그림인 법이다.

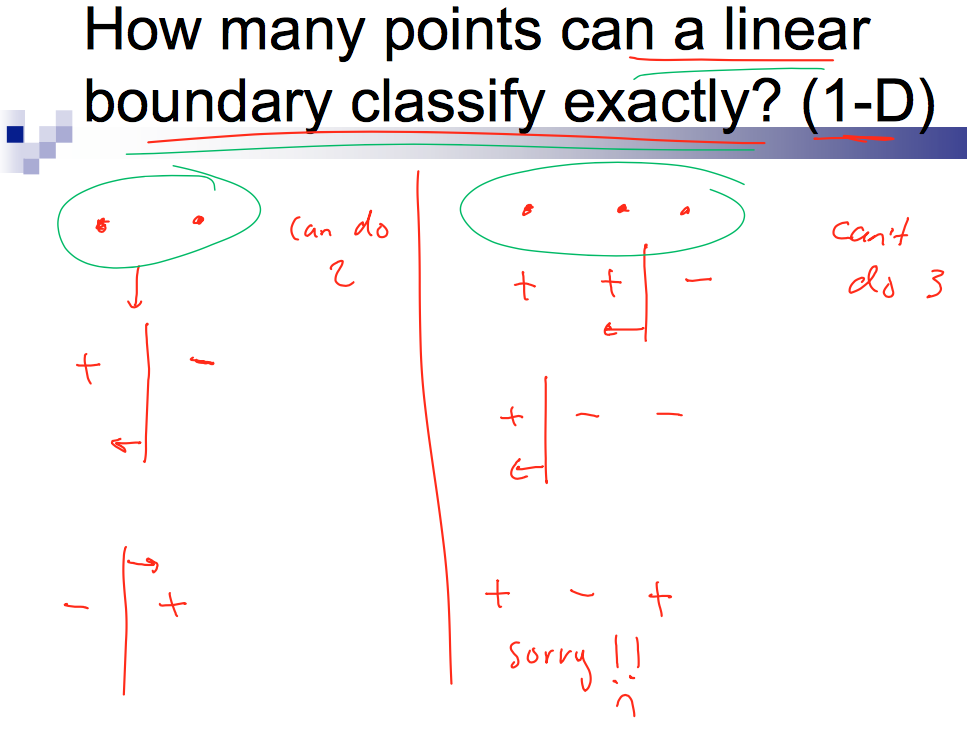
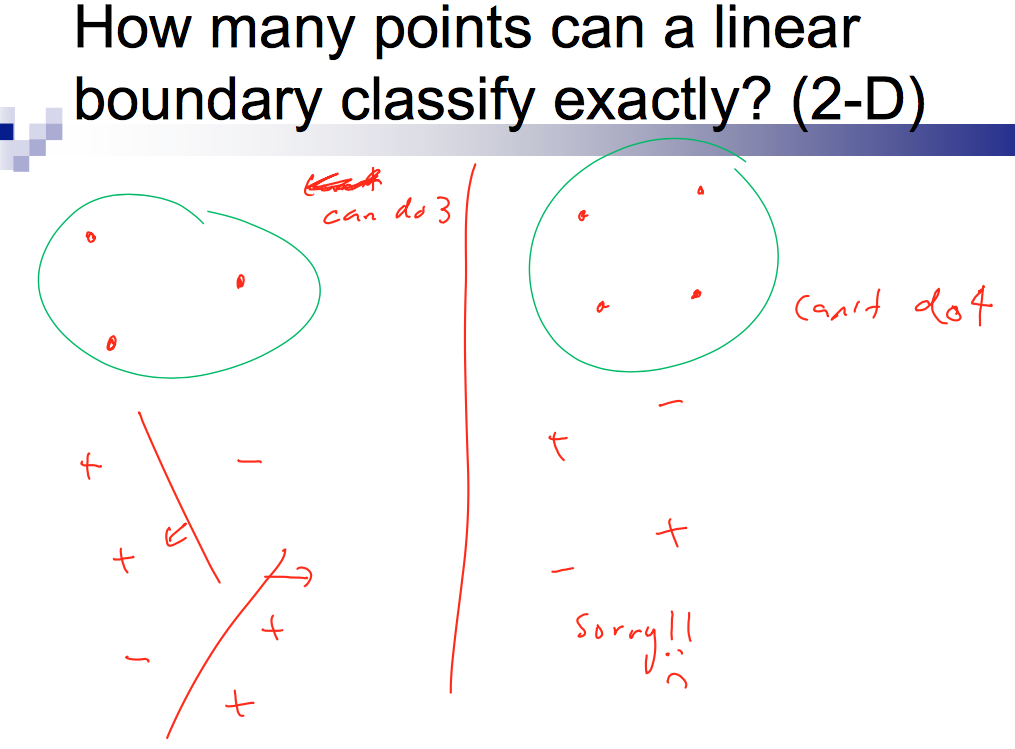
(출처: http://www.cs.cmu.edu/~guestrin/Class/15781/slides/learningtheory-bns-annotated.pdf)

또한 KNN에서 K가 1인, 즉 1-NN의 VC dimension은 무한대이다. 역시 그림으로 확인해보자. (같은 출처)

마지막으로 $k$개의 boolean variable을 가지는 decision tree는 총 $2^k$개의 leaf node를 사용해 모든 sample을 분류할 수 있으므로 VC dimension은 $2^k$이다.

이제 $|H|$를 VC(H)로 bound시켜보자. VC(H)의 값이 finite value $k$라고 가정해보자. 이는 곧 hypothesis H를 사용하여 k개의 example을 shatter할 수 있다는 의미이며, 이 경우 (binary class라고 했을 때) 총 $2^k$ 개의 labeling case가 존재한다. 여기에서 hypothesis space가 서로 다른 모든 $2^k$개의 case를 shatter할 수 있으므로 $|H| \geq 2^k$ 라는 것을 알 수 있다. 따라서 이 값에서부터 다음과 같은 매우 loose한 bound를 얻을 수 있다.

실제로 이 bound는 매우 loose하기 때문에 이 값을 그대로 사용하지는 않지만, VC(H)와 $|H|$가 어떤 관계를 가진다는 사실에 주목하자. 자세한 증명은 생략하도록 하겠지만, VC dimension을 도입하면 기존에 얻었던 finite hypothesis space에 대해 구한 PAC bound를 다음과 같이 변형할 수 있다.

위 bound에서 얻을 수 있는 intuition은 여전히 유효하다. 아래 bound가 조금 바뀌었는데, 만약 $VC(H) < 2m$ 정도로 충분히 많은 traininig dataset 하에서는 VC dimension이 작을수록, 즉 모델이 더 단순할수록 overfitting의 degree가 작아지는 Occam’s razor가 여전히 유효하다는 사실을 알 수 있다. 여기에서 bound의 우항에 존재하는 다음 term을 structure error 혹은 risk라고 부르며, empirical error 대신 이 값을 바로 optimize하는 방식으로 이론적으로 더 나은 모델을 얻는 것이 가능하다. (Structural risk minimization이라고 부른다.)

문제는 앞에서 살펴본 것처럼 VC dimension을 실제로 구하는 것이 엄청나게 어렵다는 것이다. 그러나 이 minimization을 실제로 할 수만 있다면 매우 강력한 model을 학습할 수 있는데, 실제로 SVM이 이런 방식으로 학습이 되기 때문에 매우 매력적인 model이라고 할 수 있다. 좀 더 자세한건 링크를 들어가서 확인해보면 좋을 것 같다.

정리

이 글에서는 ‘좋은 모델’이란 무엇인지 논하고, 실제로 그것들에 대한 이론적 bound를 제공하는 PAC bound에 대해 설명하였다. PAC bound는 training error, true error (test error), training data의 개수, 모델의 complexity, confidence level로 표현되는 bound로, 우리가 막연하게 ‘그럴 것이다’ 라고 생각하는 intuition들을 수식적으로 해석할 수 있게 해준다. Finite hypothesis space에 대한 증명에서부터 시작하여 최종적으로는 VC dimension까지 포함된 infinite hypothesis space에서의 PAC bound도 설명하였다. 이것 자체로는 큰 쓸모가 없어보일지는 몰라도, 모델이 얼마나 강력한지 측정하기 위해서도, 그리고 더 강력한 모델을 만들기 위해서라도 PAC라는 개념은 한 번쯤은 살펴봐야할 개념이 아닌가싶다. 참고로 이 글에서는 PAC learnable이 무엇인지 다루지는 않았다. 중요한 개념이기는 하지만, intuition 위주로 설명한 글이라서 제외하였는데, 자세한건 위키를 참고하면 좋을 것 같다.

References

  1. Kearns, Michael J., and Umesh Virkumar Vazirani. An introduction to computational learning theory. MIT press, 1994.
  2. https://en.wikipedia.org/wiki/Probably_approximately_correct_learning

변경 이력

  • 2016년 12월 18일: 글 등록

Machine Learning 스터디의 다른 글들