주어진 이미지에 대한 설명을 하는 문장, 혹은 캡션을 생성하는 문제를 image caption 문제라고 한다. 이 문제는 여러 가지 문제들이 복합적으로 얽혀있는 문제라고 할 수 있는데, 먼저 이미지가 어떤 것에 대한 이미지인지 판별하기 위하여 object recognition을 정확하게 할 수 있어야한다. 그 다음에는 detect한 object들 사이의 관계를 추론하여 이미지가 나타내는 event가 무엇인지 알아내어야 하고, 마지막으로 event를 caption으로, 즉 natural language로 재생성해야한다. 얼핏 생각하면 간단한 문제같지만 자그마치 비전과 NLP 분야의 핵심 문제들이 복합적으로 얽혀있는 복잡한 문제인 것이다. 방금 너희들이 본 건 간단해 보이지만 자그마치 3개의 퀑 기술이 합쳐진 컴비네이션! 예를 들어보자.

이 사진을 보고 우리는 ‘오바마가 청소부와 인사를 하고 있다’ 라고 바로 문장으로 풀어낼 수 있지만, 이런 문제를 푸는 알고리즘을 디자인하기 위해서는 먼저 이 사진에서 오바마와 청소부라는 핵심 object를 detect 해야한다. 그러나 아직까지는 어떤 object가 중요한지 알 수 없으므로, 먼저 복도에 있는 보좌관들, 기둥, 바닥, 뒤에 보이는 계단 난간, 전등, 복도 등등을 모두 detect 해야한다. 그러므로, caption을 만들기 위해서 가장 먼저 우리는 높은 수준의 object detection과 segmentation을 필요로 하다. 다음으로는 segmentation된 정보를 사용해서 여러 event를 알아내야 한다. ‘오바마와 청소부가 인사를 하고 있다’ ‘보좌관이 복도를 걷고 있다’ ‘한 남자가 책을 읽고 있다’ ‘사람이 기둥 뒤에 서있다’ ‘기둥 뒤에 공간이 있다’ 등의 여러 event를 추정해야하고, 그 중에서 가장 가능성이 높은 event를 판별해야한다. 마지막으로 해당 event를 설명하는 문장을 generate해야한다.
현재 caption generation 문제를 해결하는 방법들 중에서 가장 널리 쓰이고 있고, 가장 잘 동작하는 (state-of-art) 방법들은 neural network를 사용한 접근 방식들이다. Neural network를 사용하지 않은 기존 접근 방법은 크게 두 가지가 있었다. 하나는 object detection과 attribute discovery를 먼저 진행한 후에, 그것들을 사용해 미리 만들어놓은 caption template을 채우는 것이고, 또 하나는 비슷한 이미지 들의 caption 데이터를 사용해 지금 image에 적합한 caption으로 수정하는 방식이었다고 한다. Reference들을 보면 약 2010년부터 2013년 정도까지 연구가 활발하게 진행되었던 모양이지만, 지금은 전부 neural network 기반의 work에게 밀려서 사용되지 않는다고 한다.
현재 state-of-art를 찍고 있는 Neural network 기반 image description generator 모델들은 주로 2014년쯤부터 활발하게 연구가 진행되고 있다. Image caption 문제를 해결하기 위해 기존 deep learning 연구 그룹들은 마치 image를 하나의 language처럼 취급하고 실제 언어로 ‘translate’ 하는 concept을 도입해서 문제를 machine traslation의 연장선으로 바라보는 접근 방법을 취한다고 한다. 그래서 대부분의 neural network 기반의 work들은 machine translation에서 사용하는 encoder-decoder 아이디어를 활용하여 caption generation을 한다고 한다. 보통 encoder-decoder 과정에서 이미지 하나를 그대로 사용하는 대신, CNN을 사용하여 이미지 하나를 single feature vector로 표현하고, 그 feature vector를 model에서 사용하는 방식을 취하고 있다.
올해 초, 기존 state-of-art를 뛰어넘는 RNN visual attention 기반 caption generation model이 Xu, Kelvin, et al. “Show, attend and tell: Neural image caption generation with visual attention.” ICML 2015이라는 work을 통해 제안되었다. 이 논문은 기본적으로 기존의 방법들처럼 encoder-decoder 개념을 사용하지만, 추가로 visual attention이라는 개념을 caption generator에 도입하여 image caption 문제를 해결한다. Attention이란 사람이 시각 정보를 처리할 때 일부 데이터에 ‘focus’하면서 계속 focus되는 대상이 움직이는 현상을 일컫는다. 최근 RNN을 사용하여 visual attention을 반영한 새로운 모델 들이 여기저기에서 등장하고 있는데, 이는 기존 CNN 기반 접근 방법들이 모든 이미지 픽셀을 그대로 사용하는 것과 대조적이라 할 수 있다. 참고로, 이미 앞선 다른 work에서도 visual attention이라는 개념을 사용해 classification 문제를 해결했었다.
이 논문의 가장 큰 contribution은 visual attention을 “hard” attention과 “soft” attention, 두 가지 attention machanism을 제안하고 새로운 방식의 two attention-based image caption generator 모델을 제안했다는 것이다.
- “Soft” attention은 deterministic machanism으로, standard back-propagation 방법으로 train할 수 있기 때문에 전체 모델이 end-to-end로 learning된다. Soft attention model은 hard attention model의 approximation model이라고 생각하면 된다.
- “Hard” attention은 stochastic mechanism이며, reinforcement learning으로 train할 수 있다. Hard attention model은 매 iteration마다 데이터를 sampling을 해야하고, reinforcement learning과 neural network 부분이 분리되어있어 end-to-end learning이 아니라는 단점이 있다.
(+ 이 논문을 처음 읽을 때는 두 가지 모델을 ‘섞어서’ 한 모델에서 soft와 hard attention이 복합적으로 작용하는 모델을 만드는 것이라고 생각했었지만, 논문을 자세히 읽어보니, 먼저 hard attention을 제안한 후에, 이 모델의 approximation version으로 soft attention이라는 모델을 추가로 제안한 것이었다.)
그럼 이제 모델이 구체적으로 어떻게 구성이 되어있는지 자세하게 알아보도록 하자.
Image Caption Generation with Attention Mechanism: Model details
먼저 이 논문에서 제안하는 caption generation task를 정의하자. 이 논문은 caption의 길이를 $C$로, 사용할 수 있는 단어의 개수를 $K$로 고정시킨채 문제를 해결한다. 이 정의에 따라 caption을 vector $y$로 표현할 수 있다.
$$ y = \{y_1, \ldots, y_c \}, y_i \in \mathbb R^K. $$
이 식에서 각 $y_i$는 단어 하나를 의미한다. 즉, 이 논문의 목적은 ‘적절한’ caption vector $y$를 생성하는 것이다. 이 논문은 ‘적절한’ caption vector를 hard loss와 soft loss 두 가지 loss function을 사용해 정의하고 있으며, 여기에서 attention 개념이 사용된다. 자세한 설명은 아래에서 마저 설명하도록 하겠다.
이제 자세한 모델 설명을 해보자. 앞에서도 잠깐 언급했듯, 이 논문 역시 다른 기존 deep learning caption generator model들처럼 image에서 caption을 생성하는 과정을 image라는 언어에서 caption이라는 언어로 ‘translatation’ 하는 개념을 사용한다. 따라서 이 논문은 machine translation의 encoder-decoder 개념을 사용하게 되는데, encoder는 우리가 잘 알고 있는 CNN을 사용하고, decoder로 RNN, 정확히는 LSTM을 사용하게 된다. 이 논문의 핵심이라고 할 수 있는 attention 개념은 LSTM에서 사용된다.
이 논문에서 제안하는 모델을 그림으로 표현하면 다음과 같다.
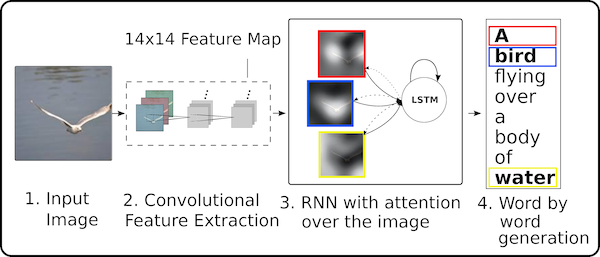
Encoder: CNN
Encoder CNN은 주어진 이미지를 input으로 받아, output으로 feature vector $a$를 내보낸다. 이 CNN의 마지막 layer는 총 $L$ 개의 filter로 이루어져있으며, 각각의 filter마다 $D$ 개의 neuron을 가지도록 설계하였다. 즉, 다음과 같이 쓸 수 있다
$$ a = \{ a_1, \ldots, a_L \}, a_i \in \mathbb R^D. $$
이 논문에서는 encoder를 위한 CNN으로 VGG network를 선택하였는데, 이 네트워크는 바로 전 글에서 다뤘으니 자세한 설명은 생략하도록 하겠다. 19 layer짜리를 사용한 것 같고, VGG11 layer로 pre-training만 시키고 fine-tunning은 하지 않은 상태로 사용했다고 한다. 당연한 얘기지만, VGG 네트워크말고도 다른 네트워크도 사용가능하다.
Decoder: LSTM
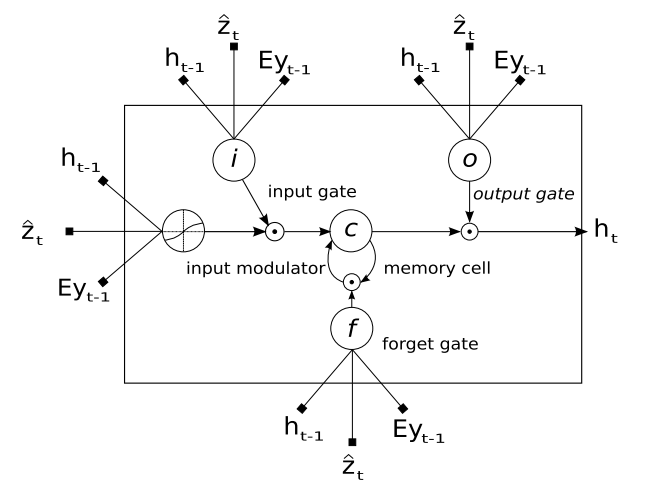
이 논문은 decoder로 LSTM을 사용한다. 이 LSTM은 매 time stamp $t$ 마다 caption vector $y$의 한 element $y_t$를 생성한다. 즉, 전체 ‘unfold’ 하게되는 시간은 caption의 길이 $C$와 같다. 즉 이 LSTM은 한 time stamp $t$ 마다 바로 전 hidden state $h_{t-1}$과 바로 전에 generate된 단어 $y_{t-1}$을 input으로 받아서 지금 time stamp에 해당하는 단어 $y_t$를 생성하는 것이다. 이 논문에서 사용하는 LSTM 모델은 다음과 같다.
LSTM에 대한 자세한 설명은 생략하도록 하겠다. 추후 다른 포스트를 통해 LSTM 자체에 대해 자세히 다뤄보도록하겠다. $T_{s,t}: \mathbb R^s \to \mathbb R^t$를 간단한 affine transformation이라고 정의해보자 ($T_{n,m} (x) = W x + b$라는 의미이다). 그러면 LSTM은 다음과 같이 간단하게 표현할 수 있다.
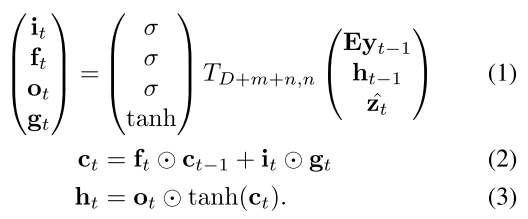
이때 1번 식의 $i_t,f_t ,c_t ,o_t ,h_t $는 각각 input, forget, memory, output, hidden state를 의미한다. 이 논문은 LSTM의 initial memory state와 hidden state를 $a$의 평균 $\bar a = \frac{1}{L}\sum_i^L a_i$을 input으로 하는 두 개의 MLP ($f_{init,c}$ $f_{init,h}$)로 estimate한다고 한다.
그럼 이제 LSTM cell 하나에 input으로 들어오는 $Ey_{t-1}, h_{t-1}, \hat z_t$에 대해 알아보자. $h_{t-1}$은 바로 전 hidden state이니 제외하고, $Ey_{t-1} $는 $t-1$ 시점에서 생성된 caption $y_{t-1}$을 embedding matrix $E \in \mathbb R^{m \times K}$로 embedding한 $m$ dimensional vector이다. $E$는 맨 처음에 randomly initialize를 한 이후 train 과정에서 update되는 parameter이다. 마지막으로 $\hat z \in \mathbb R^D$는 context vector라고 하는데, 이 context vector는 attention model들에 의해서 결정된다.
Context vector $\hat z_t$는 CNN encoder output $a$와 바로 전 hidden state $h_{t-1}$에 의해 다음과 같이 결정된다.
$$ \hat z_t = \phi (a, \alpha_t), \mbox{ where } \alpha_{ti} = \frac{\exp(f_{att}(a_i, h_{t-1}))}{\sum_{k=1}^L \exp(f_{att}(a_k, h_{t-1}) )}. $$
먼저 $\alpha_t$는 time $t$에서의 $a$의 weight vector를 의미하며, $\alpha_{ti}$는 time $t$에서의 $a$의 $i$번째 element $a_i$에 해당하는 weight value값이다. 이때 weight란, 우리가 주어진 annotation (CNN의 output) 중에서 어느 location에 focus를 맞출 것인지, 혹은 어떤 것이 중요하지 않은지를 결정하는 값으로, 모델에서 ‘attention’ 개념이 적용된 부분이다. 위의 식에서 알 수 있듯, softmax로 정의가 되기 때문에, weight $\alpha_t$의 element-wise summation은 1이다. $f_{att}$는 attention model이라는 것으로, weight vector $\alpha$를 계산하기 위한 모델이며, 이 논문은 이 모델을 hard와 soft 두 가지로 정의하였다. $\phi$ function은 주어진 $a$와 그것의 weight vector $\alpha_t$를 사용해 $\hat z_t$를 계산하기 위한 function이다. 정리해보면 다음과 같다.
$\alpha_t$: $a$의 weight vector로, 어디에 ‘attend’ 할지 결정하는 값. 모두 더하면 1.
$f_{att}$: $a$와 $h_{t-1}$을 사용해 weight vector $\alpha$를 계산하기 위한 attention model.
$\phi$: $a$와 $\alpha_t$를 받아 $\hat z$를 계산하는 mechanism (예: $\phi(a,\alpha_t) = \sum_i\alpha_{ti} a$).
마지막으로, 모델이 주어졌을 때, time $t$에서의 단어 $y_t$는 다음과 같이 바로 전 context vector $\hat z_{t-1}$와 그 동안의 LSTM의 state를 저장하고 있는 hidden state $h_t$, 그리고 바로 직전 단어 $y_{t-1}$에 관련된 확률에 의해 결정된다.
$$p (y_t | a, y^{t-1}_1) \propto \exp(L_o(E y_{t-1} + L_h h_t + L_z \hat z_t)). $$
여기에서 $L_o \in \mathbb R^{K \times m}, L_h \in \mathbb R^{m \times n} L_z \in \mathbb R^{m \times D}, E \in \mathbb R^{m \times K} $는 train과정에서 learning하는 parameter들이다.
이제 이 논문의 핵심인 attention model $f_{att}$들을 살펴보도록하자.
Stochastic “Hard” Attention
캡션 모델이 i번째 단어를 생성하기 위해 focus attention해야 하는 위치를 $s_t$라고 하는 location variable을 사용해 표현해보자. 우리가 원하는 벡터는 정확하게 focus해야하는 부분 한 부분만 값이 1이고 나머지는 전부 0인 벡터이다.
첫 번째 attention model인 stochastic “hard” attention은 attention location $s_t$를 latent variable로 취급한 다음, 이 값을 $\alpha_t$로 multinoulli distiribution parameterize시킨다. 다시 말하면, 주어진 시간 $t$에서, $s_t$의 $i$번째 element s_{ti}의 값이 1이 될 확률이 $\alpha_{ti}$이 되는 것이며, 주어진 시간 $t$에서 모든 $i$에 대해 $\alpha_{ti}$를 더하면 그 값은 1이 된다. 즉, $\sum_i \alpha_{ti} = 1$ 이다. $s_t$와 $\alpha_t$를 정의하게 되면 $\hat z_t$라는 새로운 random variable을 다음과 같이 정의할 수 있다.
$$p(s_{ti} = 1 | s_{j < t, a}) = \alpha_{ti} \mbox{ and } \hat z_t = \sum_i s_{ti} a_i. $$
우리의 목표는 주어진 feature vector $a$에 대해 가장 확률이 높은 caption $y$를 고르는 것이다. 이 작업은 간단하게 maximum log likelihood $\max_y \log p(y|a)$를 계산하는 것으로 구할 수 있는데, 이 값을 직접 계산하는 대신, 앞에서 정의한 attention location $s_t$를 사용하게 된다면 log likelihood의 lower bound를 다음과 같이 계산할 수 있으며, 이 값을 새로운 objective function $L_s$로 정의한다.
$$ L_s = \sum_s p(s|a) \log p(y|s,a) \leq \log \sum_s p(s|a) p(y|s,a) = \log p(y|a).$$
$L_s$가 log likelihood의 lower bound이므로, 이 값을 증가시키게 되면 likelihood 역시 함께 증가할 것이다. 따라서 log-likelihood의 maximum값을 구하는 대신, $L_s$의 maximum 값을 구하는 것으로 문제를 대략적으로 풀 수 있다 (하지만 엄밀하게 증명해본 것은 아니지만, 아마도 $L_s$가 local optimum으로 converge한다고 해서 원래 log likelihood가 converge할 것 같지는 않기 때문에 정확한 문제의 solution을 찾게 되는 것은 아닌 것 같다. 그러나 이미 neural network 쪽 algorithm들이 그러하듯, 정확한 답보다는 그 답을 향해 진행하는 것이 훨씬 중요하기 때문에 이 work에서는 큰 문제가 될 것 같지는 않다). Parameter $W$에 대한 $L_s$의 미분값은 다음과 같이 주어지며, 이 값을 사용하면 gradient descent를 통해 $\max L_s$ 문제를 해결할 수 있다.
$$ \frac{\partial L}{\partial W} = \sum_s p(s|a) \left[ \frac{\partial p(y| s,a)}{\partial W} + \log p(y|s,a)\frac{\partial p(s|a)}{\partial W} \right]. $$
이 미분 값을 직접 구하기 위해서는 모든 attention location $s$에 대해 summation 기호 안에 있는 연산을 계산해야하기 때문에 computation이 간단하지 않다. 이미 많은 기존 deep learning approach들에서 ‘정확한’ 값을 구하는 데에 시간이 오래걸린다면, 그냥 ‘적당히’ 빠르게 근사하는 것이 더 낫다는 것이 알려져 있는 만큼, 이 논문에서는 정확한 값을 계산하는 대신 Monte Carlo based sampling을 사용해 이 값을 다음과 같이 근사하고 있다. 이때, $\tilde s_t \sim \mbox{Multinouli}_L (\alpha)$로 주어진 값이다.
$$ \frac{\partial L}{\partial W} \approx \frac{1}{N} \sum_n^N \left[ \frac{\partial \log p(y| \tilde s^n,a)}{\partial W} + \log p(y| \tilde s^n,a)\frac{\partial p(\tilde s^n |a)}{\partial W} \right]. $$
Monte Carlo based sampling을 사용해 gradient를 근사하게 되면, 굉장히 효율적이고 빠르게 gradient를 근사할 수 있지만, 그렇게 계산된 gradient는 variance가 크기 때문에 이를 handle하기 위한 추가적인 아이디어들이 도입되게 된다. 먼저 moving average를 사용한다. 이 논문에서는 moving average baseline을 다음과 같이 이전 log likelihood들의 exponential decay를 사용한 합으로 표현하였다.
$$ b_k = 0.9 \times b_{k-1} + 0.1 \times \log p (y | \tilde s_k, a). $$
여기에 또 varinace를 줄이기 위하여 entroy term $H[s]$를 더한다. 그뿐 아니라 주어진 이미지에 0.5의 확률로 sampled attention location $\tilde s$의 값을 $\tilde s$의 기대값인 $\alpha$로 설정한다. 이 방법들을 사용하게 되면 stochastic attention learning algorithm의 robustness를 증대시킬 수 있다고 한다. 이 방법들을 모두 섞으면, 기존의 gradient는 다음과 같이 바뀐다.
$$ \frac{\partial L}{\partial W} \approx \frac{1}{N} \sum_n^N \left[ \frac{\partial \log p(y| \tilde s^n,a)}{\partial W} + \lambda_r (\log( p(y|\tilde s^n, a) - b)\frac{\partial p(\tilde s^n |a)}{\partial W} + \lambda_e \frac{H[\partial \tilde s^n]}{\partial W} \right]. $$
이렇게 구해진 식은, reinforcement learning의 update rule과 같다. 그렇기 때문에 hard visual attention을 reinforcement learning을 사용해 learning할 수 있다고 이야기하는 것이다. Action은 attention의 위치를 고르는 것이 될 것이고, reward는 log-likelihood의 lower bound인 $L_s$가 된다.
Hard attention model은 매 순간마다 $\hat z$를 ‘hard choice’를 통해 계산하게 된다. 여기에서 hard choice란, 주어진 시간 $t$에서 $\alpha$로 parameterize된 multinouilli distribution에서 $a_i$를 sampling하여 얻게되는 choice를 의미한다.
Deterministic “Soft” Attention
Hard attention은 train phase의 매 timestamp마다 attention location $s_t$를 매 번 sampling해줘야하기 때문에, 이 논문에서는 hard attention 대신 soft attention이라는 개념을 추가로 도입한다. Soft attention은 stochastic하게 매 번 sampling을 하는 대신 deterministic하게 context vecot $\hat z_t$을 계산한다. Soft attention $\phi$는 다음과 같이 표현된다.
$$\phi (\{ a_i \}, \{ \alpha_i \}) = \sum_i^L \alpha_i a_i. $$
이렇게 표현되는 이유는 $\hat z_t$의 expectation이 $\alpha, a$로 다음과 같이 직접 계산할 수 있기 때문이라고 한다.
$$ \mathbb E_{p(s_t|a)}p[\hat z_t] = \sum_{i=1}^L \alpha_{ti} a_i. $$
따라서 이 방법을 취하게 되면 전체 모델이 좀 더 smooth해지고, differentiable해지기 때문에 back-propagation을 사용해서 end-to-end로 learning이 가능하다는 장점이 있다. Deterministic attention, 혹은 soft attention 역시 앞에서 구한 likelihood $p(y|a)$를 $s_t$를 사용하여 구한 approximation을 optimizing하는 것으로 구할 수 있다. 이 논문에 따르면 $h_t$가 stochatic context vector $\hat z_t$를 tanh를 사용한 linear projection이기 때문에, $\mathbb E_{p(s_t|a)[h_t]}$를 1st order Taylor approximation하게 되면 이 값은 $\hat z_t$의 expectation인 $\mathbb E_{p(s_t|a)}p[\hat z_t]$를 사용하여 forward propagation을 한 번 진행하여 $h_t$를 구한 값과 같아진다고 한다. $n_t = L_o(E y_{t-1} + L_h h_t + L_z \hat z_t)$로 정의하고 ($p (y_t | a, y^{t-1}_1)$를 approximation했을 때 쓰인 값과 같다), $n_{ti}$를 $a_i$를 사용하여 계산한 random variable $\hat z_t$를 대입하여 구한 $n_{t}$값이라고 해보자. 이 값들을 사용하여 이 논문은 k번째 word prediction을 위한 NWGM (Normalized Weighted Geometric Mean)이라는 것을 다음과 같이 정의한다.
$$NWGM[p(y_t = k | a)] = \frac{\prod_i \exp(n_{tki})^{p(s_{ti}=1|a)}}{\sum_j \prod_i \exp(n_tji)^{p(s_{ti}=1|a)}} = \frac{\exp(\mathbb E_{p(s_t|a)}[n_{tk}])}{\sum_j\exp(\mathbb E_{p(s_t|a)}[n_{tj}])}.$$
정의에 따라 $\mathbb E [n_t] = L_o(E y_{t-1} + L_h h_t + L_z \hat z_t)$이 되므로, 이 식을 통해 우리는 caption prediction을 위한 NWGM이 expected context vector를 사용하여 approximate된다는 것을 알 수 있다. 이전의 다른 work에 의하면, NWGM은 (softmax acivation일 때만) $\mathbb E [ p(y_t = k | a)]$로 근사가 된다고 한다. 이 말은 바꿔 말하면, 모든 가능한 attention location $s_t$에 대해 구한 output의 expectation이 expected context vector $\mathbb E [\hat z_t]$를 사용하여 간단한 feedforward propagation으로 계산된다는 의미가 된다.
또한 이 논문에서는 doubly stochastic attention이라는 개념도 같이 제안한다. $\alpha$의 정의에 따라 우리는 $\sum_i \alpha_{ti} = 1$ 이라는 관계식을 가진다. 이 논문이 주장하는 것은, $\sum_t \alpha_{ti} \approx 1$ 이라는 조건을 하나 더 추가하는 것이 실제 실험결과 더 좋은 성능을 낸다는 것이다. 그 이유는 모델이 모든 이미지의 모든 부분을 전체 기간 동안 보는 것을 방해하기 때문에 더 focus된 attention이 가능하기 때문이라고 한다. 그리고 추가로, soft attention model에
결론적으로, 이 모델은 아래와 같은 negative log-likelihood를 minimize하는 방식으로 end-to-end learning을 할 수 있다.
$$ L_d = -\log (p(y|x)) + \lambda \sum_i^L \left(1 - \sum_t^C \alpha_{ti} \right)^2. $$
Experiment
다음 그림은 실제 hard attention과 soft attention이 어떻게 동작하는지 잘 보여주는 그림이다. 가장 왼쪽의 주어진 이미지에 대해 soft attnetion과 hard attention 모두 ‘a bird flying over a body of water.’ 이라는 caption을 생성했는데, soft와 hard attention 각각 경우에 대해 caption generation 모델이 어느 곳을 attend하도록 동작했는지 표현되어있다.

위의 그림이 deterministic하게 attention을 계산하는 soft attention이다. 정확한 ‘attention location’이 존재하는 것이 아니라, 하얗게 mapping된 부분을 전반적으로 attend한다고 생각하면 된다. 반면 아래에 있는 hard attention을 보면, 매 번 정확한 attention location을 고르는 것을 알 수 있다. 이 과정을 매 번 확률적으로, sampling based approximaiton을 취하기 때문에 hard attention model은 stochastic machanism이다.
다음 그림을 통해, 실제 각 word 별로 어느 곳을 attend하는지 대략적으로 확인할 수 있다.

Attend하는 위치가 비교적 굉장히 정확한 곳을 고르는 것을 알 수 있다. 좀 더 많은 예시가 gif로 이 링크에 업로드되어있으니 참고하면 좋을 것 같다. 이 논문은 성공했을 때 뿐 아니라 실패했을 경우의 attention도 아래 그림과 같이 기재하여두었다.

이 사진들을 통해 저자들은, 이 모델이 attend하는 위치는 잘 골랐으나, 각 object를 조금 잘못 classification했기 때문에 실패하는 경우가 나온다고 주장하고 있다. 예를 들어 위 실패 경우를 보면 바이올린을 스케이트 보드라고 했거나, 돛을 서핑보드라고 분류하여 잘못된 caption 결과가 나왔음을 알 수 있다.
좀 더 많은 이미지 데이터셋에 대해 hard attention과 soft attention을 사용한 caption generator의 성능은 다음 표에 잘 나타나있다. 점수는 높을수록 좋다.
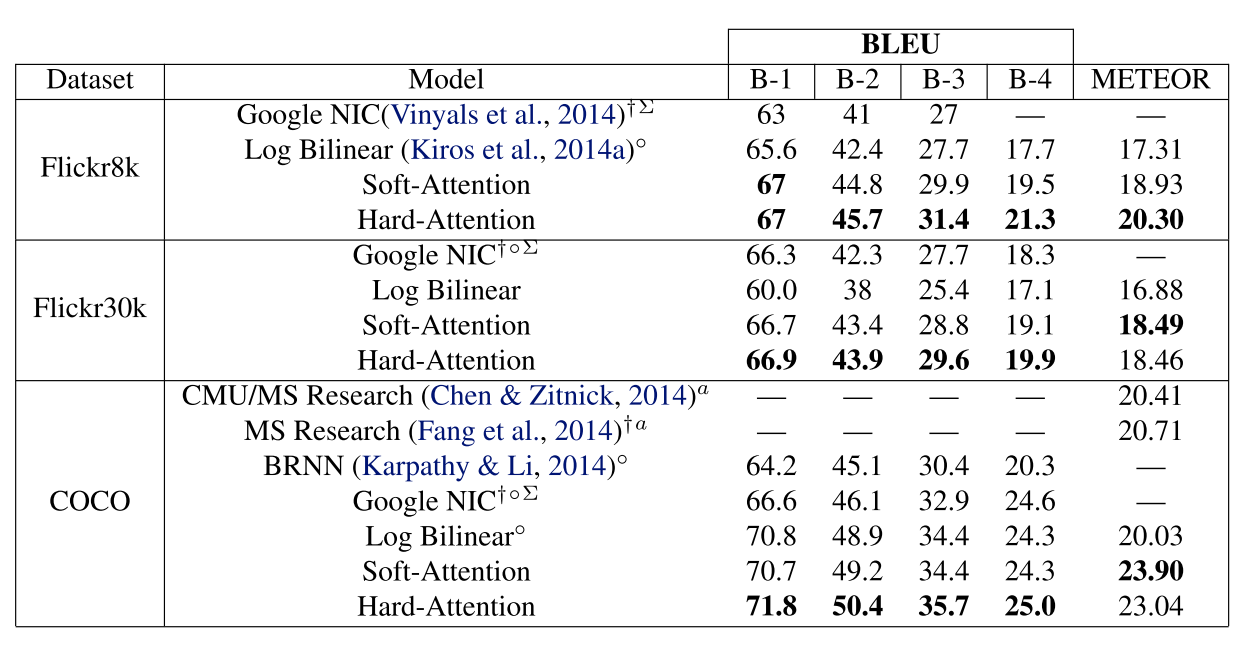
기존에 알려진 모델들에 비해 attention based model들의 성능이 훨씬 좋은 것을 알 수 있다.
Summary of Show, Attend and Tell
- Image caption 문제는 상당히 어려운 문제이며, 기존 deep learning 기법들은 machine translation에서 사용하는 encoder-decoder concept를 사용해 문제를 해결한다.
- 이 논문 역시 encoder-decoder 개념을 사용하지만, decoder에서 attention이라는 개념을 추가로 사용하여 새로운 모델을 제안하고 있다.
- Encoder는 CNN을 사용한다. 실제 실험에서는 CNN 모델로 VGG 네트워크를 선택하여 사용하고 있다.
- Decoder는 RNN, 정확히 말하면 LSTM을 사용하는데, 바로 전 state h, 바로 전 caption word y, 그리고 attention model을 통해 생성되는 context vector z가 LSTM cell의 input이 된다.
- Context vector z는 hard attention과 soft attention 두 가지 방법 중에 한 가지 방법을 선택하여 생성하게 된다. Hard attention은 stochastic machanism이고, soft attention은 deterministic machanism이다.
- Hard attention은 먼저 location variable s를 정의하고, 이것을 사용해 log-likelhood의 lower bound Ls를 계산한다. Ls를 optimization하기 위해 gradient를 구해야하는데, 이 값을 정확하게 구하는 것이 까다롭기 때문에 Monte Carlo based sampling approximation을 사용해 문제를 해결하게 된다. 이 update rule은 reinforcement learning의 update rule과 일치한다.
- Soft attention은 매 iteration마다 sampling을 하는 대신, s의 확률 alpha를 직접 사용하여 z를 계산한다.
- Attention based caption generation model은 기존 image caption generation 모델들에 비해 훨씬 좋은 성능을 보인다.