LMNN(Large Margin Nearest Neighbors) (NIPS 2006) LMCA(Large Margin Component Anaylsis) (NIPS 2007)

KNN은 machine learning에서 general하게 많이 쓰이는 알고리듬이다. 이 알고리듬은 아이디어도 매우 간단하고 구현하기도 간단하고 성능도 어느 정도 이상 나오는 꽤나 훌륭한 알고리듬이기 때문이다. 이전 글에서 distance metric learning의 대략적인 컨셉을 설명했었고, 그 중에서도 optimization을 통해 metric을 learning하는 category에 대해 간략하게 언급했었다. 이 글에서는 그런 알고리듬 중에서 LMNN (Large Margin Nearest Neighbors) 그리고 이 방법의 단점을 보완한 LMCA (Large Margin Component Analysis) 라는 알고리듬을 소개할 것이다.

LMNN - Introduction

먼저 LMNN이라는 아이디어는 2006년 NIPS에 발표된 Distance metric learning for large margin nearest neighbor classification이라는 논문에 소개된 기법이다. 이 알고리듬은 distance metric learning에 대해 설명했던 이전 글에 잠깐 언급했던 Mahalanobis Metric을 직접 학습하는 알고리듬이다. 이 Metric은 지난 번에 설명했기 때문에 자세한 설명은 생략하도록 하겠다.

이 논문에서는 거리가 제곱근 형태가 아니라 제곱 들의 합으로 표현을 했다. 즉, Mahalanobis Metric을 $D(\vec x_i , \vec x_j )=(\vec x_i - \vec x_j )^\top \mathbf M (\vec x_i - \vec x_j )$ 꼴로 표현하게 된다. 혹은 $D(\vec x_i , \vec x_j )= ||L(\vec x_i - \vec x_j)||^2 $으로 표현된다.

LMNN - Cost function

이 방법의 핵심 아이디어는, 위에서 표현한 Metric을 평가하는 Cost function을 design하고 이 function을 minimize시키는 Metric을 찾아내는 것이다. 매우 간단한 컨셉이고, 만약 운이 좋아서 optimization 문제가 반드시 하나의 global solution으로 수렴한다는 것이 보장만 된다면 가장 최고의 성능을 낼 수 있을 것이라는 것은 자명한 일이다. (이전에 작성한 글에서 이러한 좋은 문제 중 하나인 convex optimization에 대해 간략하게 언급했었다.) 자, 그러면 이 논문에서 Cost function을 어떻게 정의했는지 한 번 알아보자.

$$ \varepsilon (\mathbf L ) = \sum_{ij} \eta_{ij} ||L(\vec x_i - \vec x_j)||^2 + c \sum_{ijl} \eta_{ij} (1-y_{il}) h[ 1 + ||L(\vec x_i - \vec x_j)||^2 - ||L(\vec x_i - \vec x_l)||^2 ] $$

이때, 각 notation이 의미하는 바는 아래와 같다

${(\vec x_i , y_i )}_{i=1}^n$: training set을 의미한다. 벡터 x는 input data를, scalar y는 label을 의미한다. (binary class가 아니어도 상관없다.)
$\eta_{ij}$: $\vec x_j$가 $\vec x_i$의 target neighbor인가 아닌가를 나타내는 binary variable. 맨 처음 learning할 때 고정되는 값이며 알고리듬이 돌아가는 동안 변하지 않는 값이다.
$y_{ij}$: label $y_i$와 $y_j$가 서로 일치하는가 하지 않는가를 나타내는 binary variable이다. 역시 변하지 않는다.
h(x): hinge function으로, 간단하게 표현하면 $h(x) = max(0,x) $이다. 즉, 0보다 작으면 0, 아니면 원래 값을 취하는 함수이다.
c: 0보다 큰 임의의 상수로, 끌어당기는 term과 밀어내는 term사이의 trade-off를 조정한다. 보통 cross validation으로 결정한다.
Target neighbor: 임의의 $x_i$와 같은 label을 가진 데이터들 중에서 가장 가까운 k개의 데이터들을 의미하며 k는 사용자가 세팅할 수 있다

뭔가 복잡해보이지만, 일단 간단하게 설명하자면 앞의 항은 같은 label끼리 서로 끌어오는 term이고, 뒷 항은 서로 다른 label끼리 밀어내는 term이다. 이유는 간단한데, 먼저 앞과 뒷항 모두 포함되어있는 $\eta_{ij}$는 i와 j가 서로 target data일 때만 해당 항을 남기고, 아니면 0으로 만들어버리기 때문에 이 모든 연산은 target neighbor들에 대해서만 진행이 되게 된다. 따라서 앞의 항은 target neighbor들끼리의 거리를 의미하므로, 이 값을 minimization한다는 것은 서로 같은 label들끼리 최대한 가깝게 모아준다는 의미와 같게 되는 것이다. 그럼 오른쪽 항은? 이 항은 잘 보면 summation factor가 i,j,l인데, 일단 먼저 target neighbor i와 j에 대해서 이와는 다른 label을 가진 ($(1-y_{il})$가 0이 되지 않는) l들에 대해서 최대한 그 거리를 멀어지게 하도록 하는 항이다. 이 값은 사실 그냥 나온 값이 아니라 아래 식을 통해서 나오게 된 값이다.

$$ d(\vec x_i , \vec x_j) + 1 \le d(\vec x_i , \vec x_l) $$

LMNN - Optimization

위의 식에 대해서 간단히 언급을 하자면, 모든 i와 j들에 대해서, label이 다른 l과의 거리보다 label이 같은 데이터들끼리의 거리가 무조건 1만큼은 작아야한다는 식이다. 이 식을 살짝 전개하면 원래 cost function의 오른쪽 항과 같은 모양을 얻을 수 있을 것이다.

자! 이제 cost function을 정의했으니 optimize를 해보자. 근데 문제가 하나 있는데, 이 cost function은 convex가 아니다. 때문에 L에 대해 문제를 해결했을 때 정확한 global minimum을 찾을 수가 없게 된다. 하지만 이 논문은 아주 간단하게 이 문제를 convex 문제로 바꾸게 된다. convex 문제 중에서 semidefinite programming이라는 문제가 있는데 (간단하게 SDP라고 한다) 이 문제는 ‘어떤 조건’을 가장 잘 만족하는 positive semidefinite matrix를 찾는 문제이다. 이 문제에 대해 언급하면 포스트가 너무 길어지니 위키 링크로 대체하도록 하겠다.

그러면 이 문제를 어떻게 SDP로 바꿀 수 있을까? 해결법은 Metric을 L로 표현하는 대신에 M으로 표현하고, 이 M에 대해 문제를 푸는 것이다. 이렇게 표현하게 되면 문제가 아래와 같이 변하게 되며 이는 SDP로 간단하게 해결할 수 있는 문제가 된다.

$$ \mathbf {Minimize} \sum_{ij} \eta_{ij} (\vec x_i - \vec x_j )^\top \mathbf M (\vec x_i - \vec x_j ) + c \sum_{ij} \eta_{ij} (1-y_{il}) \xi_{ijl} \ \mathbf {subject} \ \mathbf {to:} $$

(1) $ (\vec x_i - \vec x_j )^\top \mathbf M (\vec x_i - \vec x_j ) - (\vec x_i - \vec x_j )^\top \mathbf M (\vec x_i - \vec x_j ) \geq 1- \xi_{ijl} $

(2) $ \xi_{ijl} \geq 0 $

(3) $ \mathbf M \succeq 0 $

여기에서 $\xi_{ij}$는 slack variable로, 이전 식의 hinge function과 완전히 같은 동작을 하도록 “mimick”을 하는 변수이다. 이 문제는 앞에서 언급한 SDP로 해결할 수 있는 format이기 때문에 이제 이 문제를 해결해서 적절한 $\mathbf M$을 찾아내면 우리가 찾고자하는 적절한 Metric을 찾을 수 있게 되는 것이다.

LMNN - Result

자 이제 LMNN의 실제 performance를 measure해보자. 참고로 이 알고리듬은 저자가 직접 버전관리하는 소스코드가 존재한다. 링크에서 간단하게 다운로드 받을 수 있다. 이 Metric learning이 well-working하는지 판단하기 위해서 이 논문에서는 총 4개의 알고리듬을 비교한다. (1) Euclidean distance를 사용하는 기존의 KNN (2) Optimization을 통해 얻은 Metric을 사용해 Mahaloanobis distance를 사용한 KNN (3) 앞에서 얻은 Metric을 계산할 때 사용한 Cost function을 가장 최소화시키는 label을 고르는 Energy-based classification (4) Multiclass SVM 이렇게 총 네가지 알고리듬을 사용한다. 그런데, 만약 dimension이 높은 경우에는 위의 Optimization식이 Overfitting이 될 위험성이 존재한다. 따라서 이를 방지하기 위하여 feature가 많은 문제는 PCA를 사용하여 dimension을 낮추는 작업을 하게 되는데, 이 문제가 결국 다음에 설명할 LMCA의 Motive가 된다. 아무튼 이런 방법을 사용하여 얻은 결과는 아래 표와 같다.

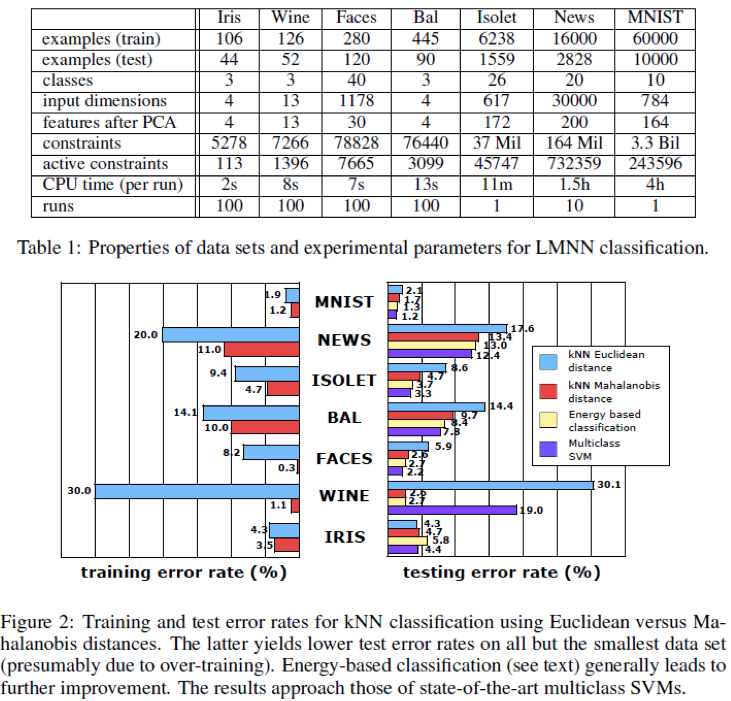
대체로 Energy-based classification이 가장 좋은 결과를 보이는 것을 알 수 있으며, 이 논문의 방법을 통해 계산한 Metric이 분명 기존의 다른 방법들보다 더 나은 방법을 제시한다고 할 수 있을 것이다. 그러나 이 방법의 근본적인 문제점이라면 Optimization으로 Metric을 구하기 때문에 Overfitting문제에 매우 취약하다는 것이며, 특히 dimension이 높고 sample개수가 적으면 이 문제가 매우매우 심각해진다. 다만, face, hand-write letter, spoken letter 등등 매우 다양한 데이터셋에 전부 개선된 performance를 보이는 것은 충분히 고무적인 결과라고 할 수 있을 것이다.

LMCA - Motivation

하지만, Feature가 1000단위가 넘어가는 high dimension 상황에서는 문제가 발생할 수 있다. 기본적으로 Optimization 문제라는 것은 언제나 Overfitting issue에서 벗어날 수 없다. 특히 LMNN이 정의한 Optimization문제는 정사각행렬 M을 학습해야하므로, dimension이 높아질수록 Optimization을 통해 찾아내야하는 항이 제곱 스케일로 늘어난다. 즉, 당장 차원이 100단위만 넘어도 찾아내야하는 항의 수가 10000개가 넘어가게 된다는 의미이다. 따라서 우리가 실제 이 문제를 적용하는 경우에, 어쩔 수 없이 dimension reduction technology를 사용할 수 밖에 없어진다. LMNN 논문에서는 PCA를 사용하여 dimension을 낮춘 이후에 Optimization문제를 풀게 되는데, 이 PCA라는 것이 물론 좋고 많은 사람들이 사용하는 dimesion reduction 방법이지만, 이 방법으로 인해 발생하는 오차가 매우 크고 실제로 더 좋은 performance를 낼 수 있음에도 불구하고 그 성능이 크게 저하되는 요인이 된다는 것이 LMCA의 Motivation이다. 실제로 PCA를 사용하게되면 Dominant한 term을 뽑아내기는 하지만 그 dimension이 낮아지거나 혹은 기존에 가지고 있는 input vector들이 bais가 된 경우에는 좋은 결과를 얻지 못할수도 있기 때문에 이 문제는 꽤나 큰 문제가 될 수 있다.

LMCA - Idea

그렇다면 어떻게 PCA등의 별다른 dimension reduction technology없이 Overfitting 문제를 해결할 수 있을까? 사실 이 논문에서 주장하는 내용은 매우 간단하다. 이전 논문인 LMNN에서 찾고자하는 Metric인 L이 dimension을 변화시키기 않는 transformation이었던 것에 반해, LMCA에서는 L을 원래 차원 D에서 더 낮은 차원 d로 보내는 L을 찾겠다는 것이다. 하지만 여기에서 문제가 생긴다. Full rank가 아닌 $ \mathbf M = \mathbf L^top \mathbf L$ 은 이제 더 이상 Semidefinite programming문제가 아니게 된다. 이유는 원래 SDP 문제에서 rank = d라는 조건이 추가되기 때문인데, 이렇게 되면 M이 convex domain이 아니게 되기 때문에 더 이상 이 문제가 convex problem이 아니게 되고, 따라서 이 문제는 더 이상 global optimum으로 수렴하지 않는다!

그렇다면 해결책은 없는 것일까? 이 논문에서는 그냥 원래 non convex인 L에 대한 cost function을 그냥 gradient descent method를 사용하여 optimize시킨다. 물론 이렇게 계산된 값은 local optimum이다. 때문에 LMNN이 무조건 global solution을 찾았던 것과 비해서 매우 performance가 떨어질 것 같지만, 저자들은 다음과 같은 2가지 장점이 있기 때문에 오히려 이 방법이 더 performance가 높다고 주장한다. 첫째, 원래 Full rank M을 찾을 때는 unknown component들이 D by D만큼 존재했었지만, 지금은 차원을 더 낮추었기 때문에 찾아야하는 값이 더 적어진다. 마치 Matrix completion의 장점과 비슷한 것이다. 둘째, 원래 LMNN은 Optimization을 할 때 parameter들이 굉장히 많은데 이런 여러 요소 없이 바로 Optimization이 가능해진다는 것이다. 물론 당연히 이 논리의 기본 가정은 high dimension data에 PCA를 사용해 low dimension으로 만들었을 때 이미 information loss가 많이 발생하거나 이미 tranining data에 overfitting되기 때문에 성능에 무조건적인 저하를 불러일으키게 되기 때문에 Optimization을 PCA를 사용하지 않은 Full dimension에 대해서 실행했다는 가정 하에 성립할 것이다.

LMCA - Results

그렇다면 결과를 한 번 확인해보자.

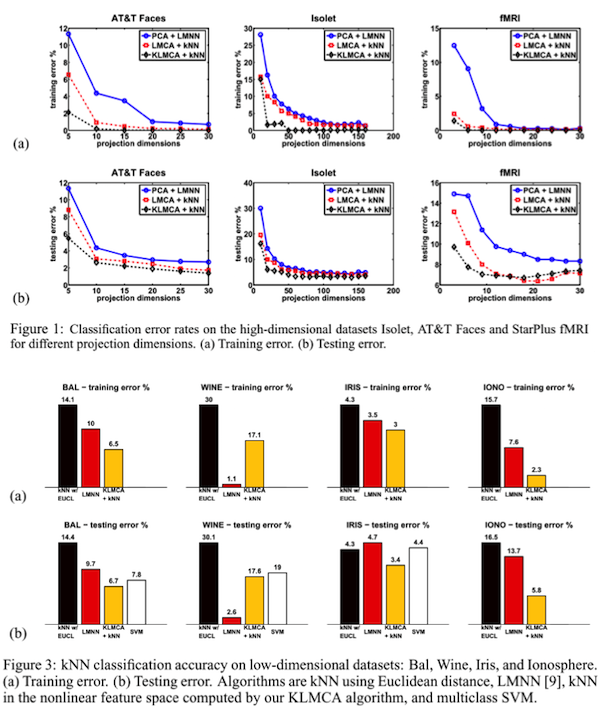
위의 그림은 high dimension dataset에 대한 것이고 아래 결과는 low dimension dataset에 대한 결과이다. 아무래도 high dimension에서는 저자들이 주장한 대로 LMNN에 비해 결과가 많이 개선된 것을 확인할 수 있다. (이 그림에서는 kernelized된… 즉 non-linear method 역시 함께 evaluation된 결과이기 때문에 LMNN과 비교해야할 대상은 linear method이다) 하지만 low dimension에 대해서는 항상 더 높은 것 만은 아니며, 일부 경우에 대해서는 LMNN이 더 좋은 결과를 보임을 알 수 있다. 즉, 이 방법은 overfitting issue가 발생했을 때 global optimum은 아니지만 그와 유사한 (그러나 절대 같다고 하거나 그와 유사하다고 할 수도 없는) local optimum을 찾는 방법이기 때문에, overfitting issue가 적은 low dimension에서는 LMNN보다 성능이 떨어질 수도 있는 것이다.

Non-linear LMNN, LMCA

지금까지 언급한 방법들은 모두 ‘linear’한 transformation을 찾는 문제였다. 하지만 세상에는 엄청나게 많은 non-linear metric이 존재하며, 분명 linear보다 성능이 더 좋은 non-linear metric을 찾을 수 있을 것이라고 생각할 수 있다. 그렇다면 이 논문들에서 과연 그런 방법을 다루지 않을까? 일단 LMNN은 NIPS에 제출된 원래 논문에는 non-linear problem이 언급이 되어있지않지만, 나중에 GB-LMNN (Gradient Boost LMNN)이라는 방법을 소개하며, 이 방법의 powerful함은 LMNN code에서 직접 확인할 수 있을 것이다. 이 방법은 Gradient Boost라는 방법을 사용하여 non-linear metric을 찾아내는데, 문제는 이 방법이 non-convex하다. 따라서 초기값에 따라서 그 결과가 상이하게 달라지게 되는데, 해당 논문에서는 LMNN을 통해 학습한 L을 초기값으로 사용하여 Optimum값을 찾는 아이디어를 제시해 L의 성능을 개선시킨다고 명시되어있다. 분명 Optimize를 시키기 때문에 본래 값보다는 더 좋은 값으로 수렴할 것이며 성능도 어느정도 올라갈 것이라고 예측이 가능할 것이다. Gradient boost는 regression tree라는 것을 학습하여 non-linear transformation을 찾아내는데, 이 tree의 node개수나 level등등을 어떻게 학습시킬 것이냐에 따라 그 running time과 overfitting issue가 결정되는 듯 하다. 더 자세한 점은 해당 논문을 읽어보기를 권한다.

또한 LMCA는 원 논문에 non-linear method까지 언급이 되어있다. 본래 아이디어 자체가 그냥 gradient descent를 사용해서 local optimum L을 찾는 문제이기 때문에 kernel에 대해서도 이 문제를 동일하게 풀 수 있는 듯하다. 다만 그 update rule을 어떻게 결정하느냐의 문제가 있는지 논문에서 cost function의 gradient방향으로 내려가는 것이 올바른 update rule이라는 것을 Lemma를 증명해놓았다. 아무튼 당연한 얘기지만 이 방법이 linear method보다 그 결과가 좋다. 자세한 점은 마찬가지로 해당 논문을 참고하길 바란다.

Conclusion

KNN은 엄청 직관적인 method이지만 분명 powerful하고 easy to implement한 방법이다. 또한 이론적으로 그 bound가 가장 optimal한 case에 bayes risk와 같다는 것이 증명이 되어있기 때문에 사실 굉장히 좋은 방법이라고 할 수 있다. 그러나 실제 우리가 이 방법을 적용하는 대부분의 상황에서는 metric learning이 performance에 크게 영향을 끼칠 수 밖에 없다. LMNN과 LMCA는 Optimization problem을 solve함으로써 상당히 좋은 결과를 얻어낼 수 있는 좋은 Metric learning알고리듬이라고 할 수 있다. 물론 이 방법들에는 overfitting issue가 존재하고, 이 때문에 적절한 상황이 아닌 경우에 특히 high dimension, low sample problem에서 well working하지 않는다는 단점이 존재하기는 한다. 하지만 저자가 구현한 implement하기 좋은 matlab code도 존재하고, 여러모로 괜찮은 방법이 아닌가 하는 생각이 든다.

References

K.Q.Weinberger,J.Blitzer,andL.K.Saul(2006) .InY.Weiss,B.Schoelkopf, and J. Platt (eds.), Distance Metric Learning for Large Margin Nearest Neighbor Classification, Advances in Neural Information Processing Systems 18 (NIPS-18). MIT Press: Cambridge, MA.
Torresani, L., & Lee, K. (2007). Large margin component analysis. Advances in Neural Information Processing
Kedem, D., Xu, Z., & Weinberger, K. (n.d.). Gradient Boosted Large Margin Nearest Neighbors