Coursera Neural Networks for Machine Learning Week2 - Perceptron

들어가기 전에

이 글은 Geoffrey Hinton 교수가 2012년 Coursera에서 강의 한 Neural Networks for Machine Learning 2주차 강의를 요약한 글이다. 첫 주 강의에서 Neural Network란 무엇이며 어떤 종류의 Neural Network들이 있는지 등에 대해 간략하게 다뤘다면, 이 강의에서는 가장 오래된 Neural Network 중 하나인 Perceptron을 설명하는 내용이 주가 된다.

An overview of the main types of neural network architecture

이전 글에서 Neuron들에는 어떤 종류가 있을 수 있는가 다뤘었다. 대충 linear neuron, linear threshold neuron, binary neuron, binary threshold neuron, sigmod neuron 등이 있었다. 그렇다면 neuron들로 구성된 neural network에는 어떤 type들로 구분되는가도 간략하게 알아보도록 해보자.

일단 가장 간단한 형태의 network로 Feed-forward neural network가 존재한다. 가장 일반적으로 쓰이고 실제 어플리케이션에 적용되는 neural network들도 대부분이 feed-forward라고 한다. 이 네트워크는 상당히 간단한 구조인데, 첫 번째 layer는 input이며 가장 마지막 layer는 output이다. 그리고 중간의 input과 output으로 관찰되지 않는 영역을 “hidden” layer라고 하는데, 당연히 visuable하지 않으므로 (우리가 직접 관측하는 영역이 아니므로) hidden이라고 불리는 것이다. 만약 hidden layer가 하나보다 많이 존재한다면 이 network는 “deep” neural network라고 불린다.

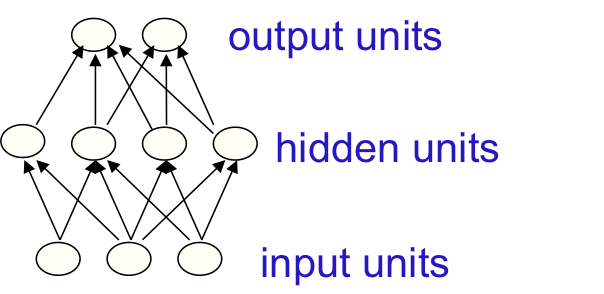
위의 그림이 Feed-forward neural network의 간단한 예시이다. (이 그림은 Hinton 교수의 slide에서 가져왔다.)

이보다 조금 더 복잡한 network로는 Recurrent network라는 것이 존재한다. “Recurrent”라는 이름이 붙은 이유는 graph에 cycle이 존재하기 때문인데, 이 말인 즉슨, 이 network에서는 arrow를 계속 따라가다보면 어느 순간 같은 장소를 계속 돌고 있을 수도 있다는 의미이다. 당연히 일반적인 방법으로 이것을 학습하는 것은 매우 복잡한 일이고 어려운 일이다. 그럼에도 일단 이 네트워크는 가장 “biologically” 현실적인 네트워크라고 한다.

위와 같이 directed cycle이 존재하는 경우 recurrent network라고 하는데, 이 방법을 사용해서 sequential data를 modeling할 수 있다고 한다. 그런 행위가 가능한 근본적인 이유는 이 방법 자체가 일종의 시간 축으로 very deep한 network로 치환이 가능하기 때문이다. 그림으로 보면 아래와 같은 형태가 된다.

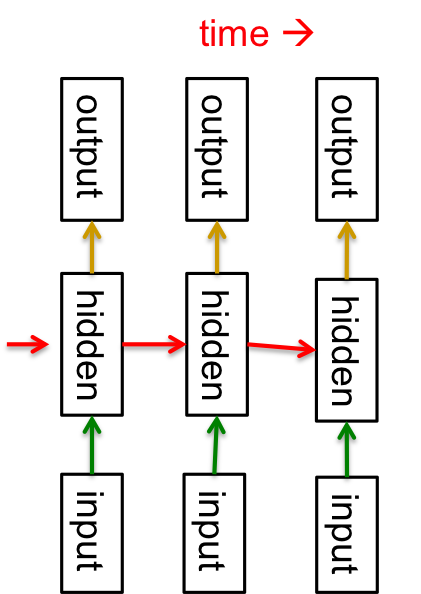
자 다시 위의 그림을 보면서 차근차근 설명하자면, 위의 그림은 매 시간마다 하나의 hidden layer를 가지는 네트워크이며, 각 hidden layer는 그 다음 hidden layer에 무언가 information을 주는 형태이다. 즉, 자기 자신이 자기 자신에게 정보를 주는 cycle이 존재하는 형태이며, 매 시간마다 input과 output이 존재한다고 생각할 수 있다. 이런 이유로 recurrent network를 이런 형태의 network로 치환하여 생각할 수 있는 것이다. 당연히 실제로 학습하기는 무지하게 어렵지만, 실제 이런 network가 계속 연구가 되고 있으며 2011년 Ilya Sutskever의 연구에서 이런 형태의 network를 사용해 wikipedia의 단어들을 학습해 자동으로 sentence를 generate하는 모듈을 만들어서 실행시킨 결과, 다음과 같은 문장을 얻었다고 한다.

In 1974 Northern Denver had been overshadowed by CNL, and several Irish intelligence agencies in the Mediterranean region. However, on the Victoria, Kings Hebrew stated that Charles decided to escape during an alliance. The mansion house was completed in 1882, the second in its bridge are omitted, while closing is the proton reticulum composed below it aims, such that it is the blurring of appearing on any well-paid type of box printer.

물론, 완전한 형태의 영어는 아니지만, 매 순간 단 하나의 단어만을 generate한 결과임에도 불구하고 엄청나게 뛰어난 성능을 보이고 있음을 알 수 있다. 일반적으로 이런 sentance generate을 위한 모델은 무지무지 복잡하고 여러 단어를 동시에 학습하거나 생성하거나 하는 등의 과정을 거치는데 이 논문에서는 오직 단어를 하나씩만 생성했음에도 꽤 그럴듯한 영어가 나왔다는 점이 고무적이라는 것이다.

마지막으로 Symmetrically connected network가 있다. 이 network는 recurrent network의 special한 case라고 보아도 무방한데, 간단히 말하자면 이전의 neural network들은 모두 directed graph였지만, 이 symmetrically connected network는 undirected graph이다. 즉, 각 layer간에 symmetric한 edge, 다시 말하자면 양 방향으로 서로 같은 weight를 가지게 된다는 의미이다. 이런 network는 energy function이라는 것을 도입하면 recurrent network보다 훨씬 분석하기가 용이하며, performance도 powerful하다. 만약 hidden unit이 없다면 Hopfield network라고 부르며, hidden layer가 존재하면 Boltzmann machine 이라 부르는데, 이 녀석은 나중에 언젠가 다루게 될 Deep network에서 이 Boltzmann machine을 restrict시킨 형태인 Restricted Boltzmann Machine (RBM)을 설명할 때 다시 한 번 자세하게 다룰 예정이다. (Coursera lecture로 따지면 거의 맨 끝 즈음이다.)

Perceptrons: The first generation of neural networks

자, 어쨌거나 2주차 강의의 핵심은 바로 perceptron이다. 이 녀석은 가장 오래된 neural network 중 하나이며, 특정 상황에서는 정말 outperform한 결과를 보여주지만 그 한계가 분명한 알고리듬이다. 1690년대 Frank Rosenblatt에 의해 제안된 알고리듬으로 Artificial neural network을 태동하게 한 알고리듬이지만, 그 한계가 너무나 명백하여 한 동안 neural network 연구 자체가 이뤄지지 않게 한 원인이 되기도 한다. 1969년 Minsky가 perceptron이 linear가 아니면 아무것도 할 수 없다는 것을 증명했는데 (단적인 예로, xor조차 학습하지 못한다) 당시 multi layer perceptron에도 이 방식이 적용될 것이라 다소 과도한 추측을 하는 바람에 neural network 연구 자체가 한 동안 메일 스트림이 아니었다. 아무튼, perceptron은 엄청 간단한 feed-forward network의 일종이다. 무지무지 간단하게 그림 하나로 표현하면 아래와 같다 (그림은 google image에서 찾은 그림..)

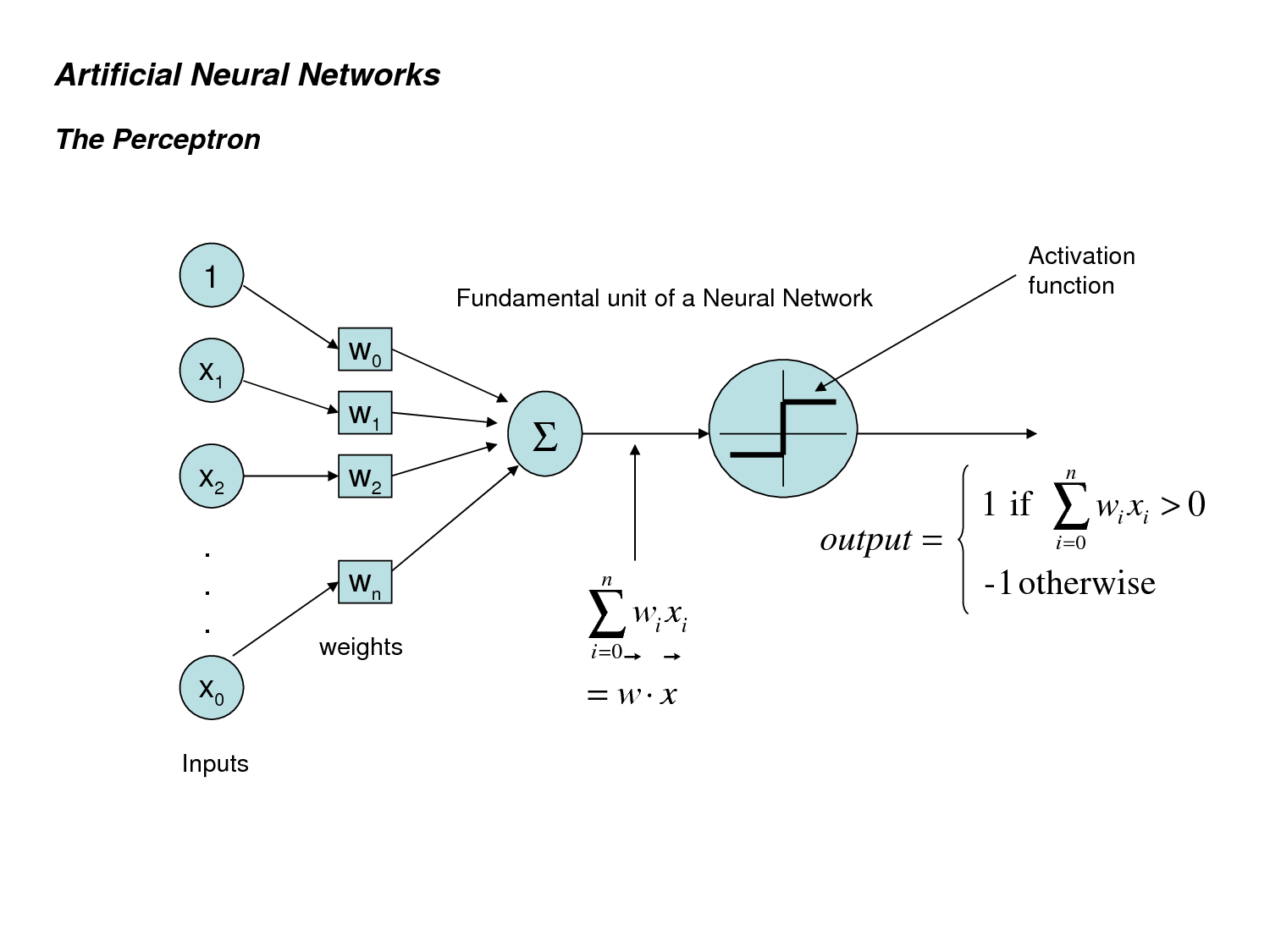
하나하나 간단하게 설명해보자. 일단 input layer가 있다. 맨 아래 $x_o$는 $x_n$의 오타로 추정된다. 맨 위의 1은 bias를 위한 term이다. 이전 글에서 bias에 대해 설명한 것을 기억하는지? input과 weight를 linear combination 형태로 정리하고 나서 거기에 상수 항으로 더해지는 값이 bias이다. 즉, input과 상관없이 늘 더해지는 값으로, $b = 1 \times w_o$ 라고 봐도 무방한 것이다. 아무튼, 지금은 간단하게 input layer에서 원래 input vector x와 bias term 1을 weight vector와 곱한 형태인 $z = \sum_i w_i x_i$를 계산했다고 간단하게 생각해보자. perceptron의 decision rule은 간단한데, 방금 계산한 값이 어떤 threshold를 넘으면 값을 activate, 넘지 못하면 값을 deactive 시키는 것이다. 간단하게 얘기하면 perceptron에서는 binary threshold neuron을 사용하는 것이다. 이 threshold를 결정하는 것은? 바로 bias가 그 역할을 하게 된다. 그러므로 이 알고리듬에서 “learning”하는 것은 weight와 bias가 될 것이다. 음.. 뭔가 간단하게 bias는 무시하고 weight만 학습하는 방법은 없을까? 앞에서 bias를 weight로 간단하게 치환한 방법을 사용하면 이렇게 문제를 간단하게 만드는 것이 가능해진다. 원래 input vector에 value 1을 추가하여 마치 input vector가 하나 더 있고, 그 component에 대한 weight가 존재하는 것처럼 trick을 쓰는 것이 가능해진다. 따라서 bias도 weight와 같은 방법으로 자연스럽게 learning할 수 있게 되고, 더 이상 threshold에 대해 고민할 필요가 없어진다!

perceptron이 weight를 학습하는 방법도 매우 간단하다. input vector가 들어왔을 때, 현재 weight로 맞는 값이 나온다면 weight는 update되지 않는다. ($w_{t+1} = w_t$) 만약 1이 나와야하는데 0이 나온다면 weight vector에 input vector를 더해준다. ($w_{t+1} = w_t + v$) 만약 0이 나와야하는데 1이 나온다면 weight vector에서 input vector를 빼주는 방식으로 weight를 update한다. ($w_{t+1} = w_t - v$)

조금 더 잘 describe해보자면, input x에 대해서 output(label) y는 다음과 같은 수식으로 표현된다 -아래 수식에서는 편의를 위해 y = {-1,1} 이라고 하자-

$$ y = sign( \sum_{i=0}^n w_i x_i ) \hskip 1em where, x_0 = 1 \hskip 0.3em and \hskip 0.3em w_0 = -b$$

즉, label y는 vector w와 x의 inner product로 나타낼 수 있으며 이 때 bias b는 $x_0 = 1$, $w_0 = -b$라는 형태로 간단한 weight vector와 input vector의 linear combination으로 표현할 수 있게 되는 것이다. 이 때 update rule은 다음과 같다

$$ w_{t+1} = w_t + y_n x_n, \hskip 1em when \hskip 0.3em misclassified $$

misclassified가 발생했을 때만 update가 일어나며, update rule은 원래 y와 x를 곱해서 원래 vector에 더해주는 것이다. 즉, 1이 나와야하는데 -1이 나왔다면 w에 +x를 취해주고, -1이 나와야하는데 1이 나왔다면 w에 -x를 취해주는 것이다. 그리고 step을 진행시키면서 (t가 점점 증가하면서) misclassified point가 발견될 때 마다 이 알고리듬을 반복한다. 이렇게 설명하면 조금 더 깔끔하게 수식적으로 설명이 가능해진다.

A geometrical view of perceptrons

위와 같은 update rule이 선택되는 이유는 무엇인가? 왜 하필이면 input vector를 합해야할까? 이런 질문들은 모두 geometric하게 해석할 수 있다. feature가 n개일 때, input vector와 weight vector는 some n-dimensional vectors이므로, 이 vector들이 존재하는 vector space를 정의하는 것이 가능해지기 때문이다. 여기에서는 weight space라는 새로운 형태의 space를 정의해서 perceptron을 해석할 것이다. 따라서 원래 수식과 대조하여 생각해보면 우리가 궁극적으로 찾고자하는 truth weight vector는 올바른 answer에 대한 어떤 hyperplane일 것이라는 것도 충분히 추측할 수 있다. 무슨 소리냐하면, input vector와 weight vector의 inner product의 sign이 y를 결정한다는 의미는, 곧 그 내각이 90도보다 크냐 작으냐로 생각할 수 있고 (물론 n-dimensional vector에서는 각도 개념이 정의하기 나름이지만) 아마도 대부분의 input vector들에 대해서 올바른 label을 가지게 하는 어떤 hyperplane이 우리가 찾고자하는 궁극적인 weight vector들이라는 것이다. 그림으로 설명해보자.

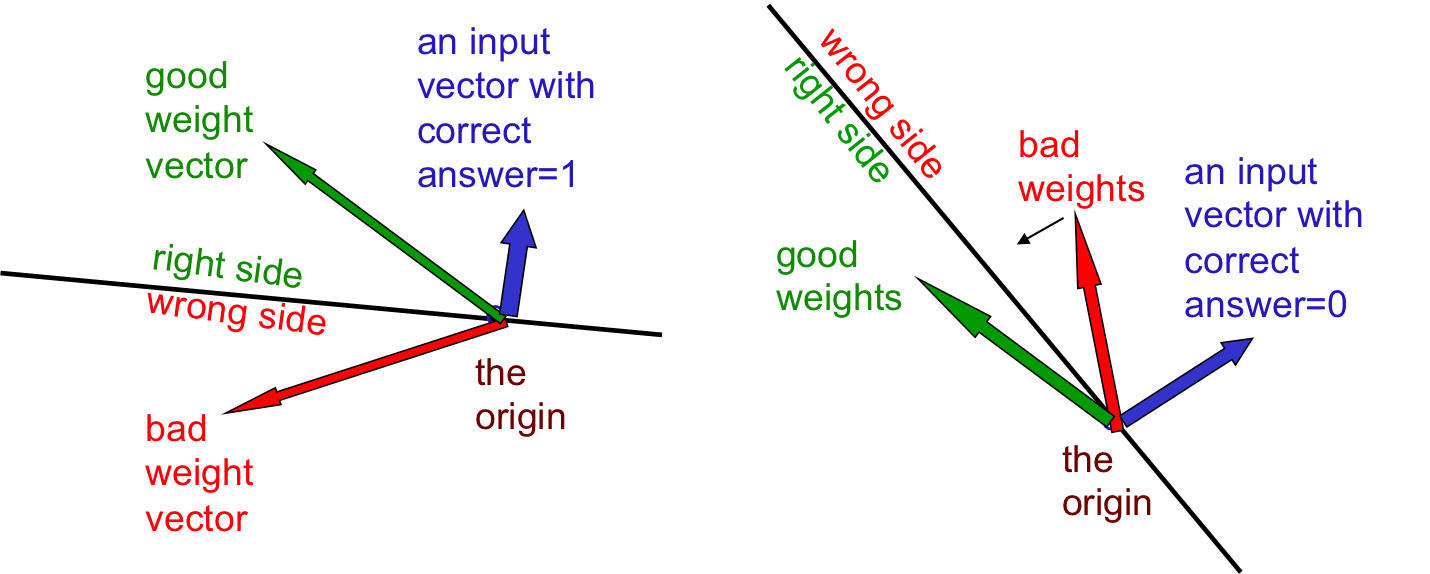
위의 그림에서 correct answer가 1이라면 input vector와 weight vector의 inner product를 구했을 때 올바른 값이 나오기 위해서는 당연히 초록색 vector이어야한다는 사실을 알 수 있을 것이다. 이유는 위에서 언급했듯 사이각이 90도 보다 작은 두 벡터의 inner product는 언제나 0보다 크기 때문이다. 따라서 input vector에 orthogonal한 plane을 그리고, 그 plane을 기준으로 weight vector가 올바른 곳에 존재하는지 그렇지 않은지 간단하게 알 수 있을 것이다. 다음에는 correct answer가 0인 경우 (-1인 경우)를 살펴보자. 이 경우에는 두 벡터의 사이 각이 90도보다 커야하므로, input vector에 orthogonal한 plane의 반대 부분이 올바른 weight vector의 위치가 됨을 알 수 있다. 그렇다면 올바르지 않은 (misclassified된) weight vector를 올바른 영역으로 옮기기 위해서 어떤 행동을 취할 수 있을까? 조금만 생각해보면 정말 간단한 vector sum으로 hyperplane의 반대쪽으로 보낼 수 있다는 것을 알 수 있다. 왼쪽 상황에서는 빨간 벡터를 초록 벡터로 만들기 위해서 간단하게 빨간 벡터에 파란 벡터를 대해주면 되고 ($w_{t+1} = w_t + v$) 오른쪽 경우는 빼주면 된다 ($w_{t+1} = w_t - v$). 이런 이유로 벡터를 더하고 빼는 것 만으로 weight가 ‘개선’되었다고 할 수 있는 것이다. 만약 weight들이 올바르게 learning되었다면 우리는 아래와 같은 결과를 얻게 될 것이다.

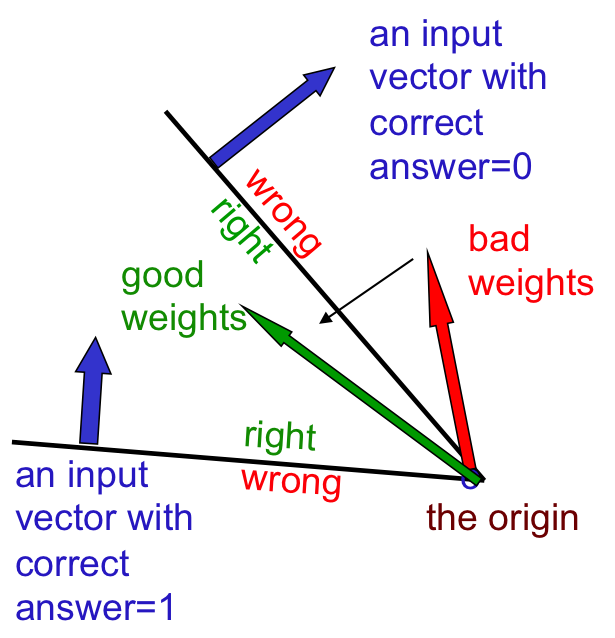
즉, 올바른 weight는 서로 다른 input vector들이 모두 well-classified되게하는 어떤 vector임을 알 수 있다. Training을 하면서, 우리가 찾아내는 값은 바로 가장 올바른 weight vector를 찾는 것이며, 위의 그림에서 볼 수 있듯 우리는 space 위에 여러 hyperplane을 그릴 수 있고, 이를 이용하여 good weight들이 위치하는 hypercone을 그릴 수 있다. 재미있는 점은, 이 cone위의 vector는 convex하다는 것이다 (그 어떤 벡터 두 개를 골라도 그 중간에 존재하는 모든 벡터들이 cone안에 존재한다) 즉, 우리가 만약 이 문제를 convex하게 해결한다면 항상 우리는 global optimum값을 찾을 수 있게 되는 것이다.

Why the learning works

위에서 geometric view로 perceptron을 서술하였으니, 이번에는 도대체 왜 이런 알고리듬이 작동하는지 알아보도록 해보자. 사실 엄밀한 수학적 증명이 강의에 나오지 않기 때문에 복잡한 증명은 생략하고, 간단하게 그림으로 설명해보도록 하겠다. 일단 아래 그림을 보면서 진행해보도록하자.

아래 그림의 상황은 current weight vector와 any feasible한 weight vector 사이의 거리 $d_a^2+d_b^2$을 고려해보도록 하자. 만약 이런 상황에서 perceptron이 misclassified된다면, learning 알고리듬이 current vector를 조금 더 feasible한 weight vecotr에 가까워지도록 움직여줄 것이다. 하지만 문제가 생기는데, 거의 plane에 근접하게 있는 point를 생각해보자. 이 그림에서는 노란색 점이 그것이다. 이 점은 분명 조금 더 “feasible vector”에 가깝게 움직여질 필요성이 있지만, 노란색 점은 이미 feasible region 위에 위치하기 때문에 아무리 알고리듬이 running하더라도 절대로 feasible point 근처로 옮겨지지 않는 것이다. 이런 문제점을 해결하기 위해서 ‘margin’이라는 컨셉이 도입된다.

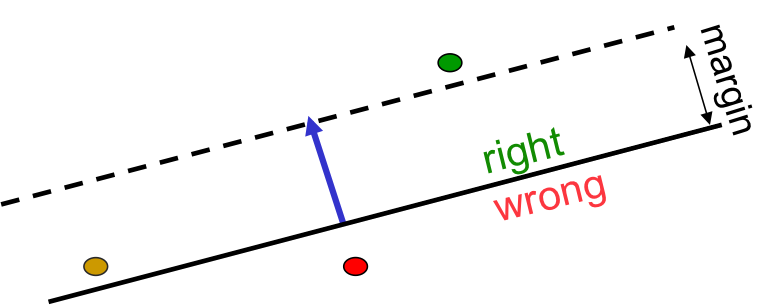
위의 그림에는 margin이라는 것이 표현되어 있는데, 이 margin은 feasible한 weight vector를 조금 더 strict하게 정해주는 역할이다. 즉, feasible region을 plane에서 margin 보다 더 멀리 떨어진 위치로 정의하고, 이 region안에 존재하는 vector를 “generously feasible”한 weight vecotr로 정의하는 것이다. 즉, 이제는 노란색 vector가 margin보다 더 조금 떨어져 있기 때문에 더 이상 “feasible”한 vector가 아니므로 perceptron algorithm을 사용하여 이 벡터를 옮기는 것이 가능해지는 것이다.

이런 가정하에, 이 알고리듬이 converge한다는 것이 증명가능하다고 하는데, 구체적인 증명과정은 강의에 설명되어있지는 않고, 간단한 아이디어만 서술되어있다. 그 아이디어는 크게 세 개인데, perceptron이 feasible region에 존재하지 않는 weight vector를 update하고, update마다 missclassified vector와 feasible vector사이의 distnace가 감소되는 방향으로 update가 될 것이다. 또한 이 거리는 매 번 최소한 input vector의 lenght의 제곱근만큼은 감소한다는 것이다. 따라서 유한한 숫자의 iteration안에 weight vector가 반드시 feasible region안에 위치하게 된다는 것이다. 물론 이 모든 것은 그러한 feasible region이 존재하는 경우에만 동작하는 것은 당연할 것이다.

What perceptrons can’t do

하지만 perceptron은 너무나도 명확한 한계점이 존재한다. input vector가 binary이기 때문에 모든 input을 binary feature로 바꾸어야한다는 점도 문제이지만, 가장 큰 문제는 linearly separable하지 않은 dataset들은 learning할 수가 없다는 것이다. 엄청나게 간단한 예를 살펴보도록하자. xor은 binary 연산의 가장 기본적인 연산 중 하나이다. 두 값이 같으면 0, 다르면 1을 return하는 것인데, 이를 2차원 평면에 포함하면 아래와 같은 상황이 되어버린다.

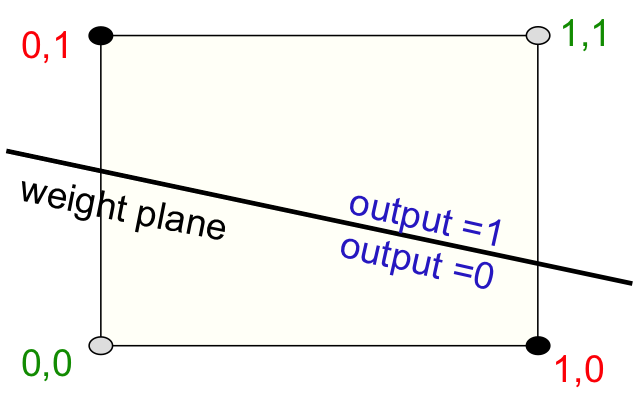
초록색 label이 된 점들이 output이 0인 점들, 빨간색 점들은 ouput이 1인 점들이다. 당연하게도, 이 점들을 구분할 수 있는 ‘단 하나의’ plane은 존재하지 않는다. 단순히 이 결과만 보더라도 perceptron이 얼마나 제한적인 상황에 대해서만 동작하는지 분명하게 알 수 있다. 또한 perceptron의 decision making은 summation으로 이루어지기 때문에, 만약 n 차원 벡터의 패턴이 아래와 같으면 구분이 불가능한 것이다

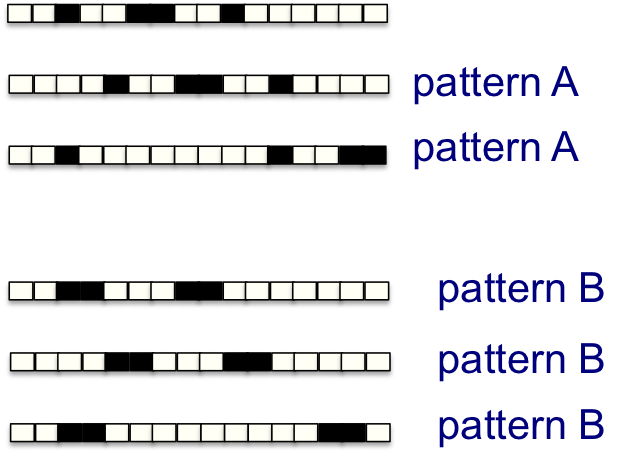
pattern A는 점들의 set이 1, 1, 2로 존재해야하고, pattern B는 2, 2로 존재해야하는데 둘 다 합이 4이기 때문에 perceptron으로는 이를 구분하는 것이 불가능하다.

이렇듯 perceptron은 그 한계가 너무나 명확하다. 그러나 이는 single layer perceptron에 한정된 문제이지 neural network 전체의 문제는 아니다. 이를 해결하는 방법은 생각보다 간단한데, 바로 hidden unit을 learning하는 것이다. multiple hidden layer는 neural network가 더 이상 linear하지 않고 non-linear하게 해주는 역할을 하는데, non-linear해지기 때문에 learning하기가 힘들어지지만, 만약 learning이 가능하다면 그 만큼 powerful해지는 것이다. 그렇다면 이런 net을 learning하는 것은 가능할까? 결론부터 얘기하자면 엄청나게 어렵다. 때문에 이에 대한 연구가 활발히 이루어지고 있으며 꽤 성공적인 결과들이 존재한다. 또한 hidden layer의 weights를 learning하는 것은 feature를 learning하는 것과 같아지기 때문에 더 이상 feature에 대한 문제도 없어지고, 여러모로 hidden unit을 learning하면 그 한계를 깰 수 있는 network가 될 수 있는 것이다.

Coursera Neural Networks for Machine Learning

다른 요약글들 보기 (카테고리로 이동)

Lecture 1: Introduction
Lecture 2: The Perceptron learning procedure
Lecture 3: The backpropagation learning proccedure
Lecture 4: Learning feature vectors for words
Lecture 5: Object recognition with neural nets
Lecture 6: Optimization: How to make the learning go faster
Lecture 7: Recurrent neural networks
Lecture 8: More recurrent neural networks
Lecture 9: Ways to make neural networks generalize better
Lecture 10: Combining multiple neural networks to improve generalization
Lecture 11: Hopfield nets and Boltzmann machines
Lecture 12: Restricted Boltzmann machines (RBMs)
Lecture 13: Stacking RBMs to make Deep Belief Nets
Lecture 14: Deep neural nets with generative pre-training
Lecture 15: Modeling hierarchical structure with neural nets
Lecture 16: Recent applications of deep neural nets