Coursera Neural Networks for Machine Learning Week3 - Backpropagation

들어가기 전에

이 글은 Geoffrey Hinton 교수가 2012년 Coursera에서 강의 한 Neural Networks for Machine Learning 3주차 강의를 요약한 글이다. 이 렉쳐에서는 Perceptron의 한계를 극복하기 위해 도입된 multi-layer feed forward network를 learning하는 algorithm인 backpropagation algorithm에 대해서 다룬다.

Learning the weights of a linear neuron

Lecture 2의 마지막에서 다뤘던 perceptron의 가장 큰 문제점은 문제가 조금만 복잡해지거나, linear하게 표현되지 않는 문제는 올바른 결과로 수렴할 수 없다는 것이었다. 예를 들어서 엄청나게 간단한 로직인 xor은 perceptron으로 learning될 수 없다. 이런 문제를 해결하기 위해 multi-layer feed forwad neural network의 필요성이 대두된다. 일단 우리는 기존의 perceptron algorithm으로는 해당 문제를 해결할 수 없다는 것을 알고있으므로, 무언가 다른 알고리듬을 한 번 고안해보도록 하자. 가장 간단하게 생각할 수 있는 알고리듬은 어떤 error function을 정의하고 그 error를 minimize시키는 network를 learning하는 것일 것이다. 그렇다면 어떤 error function을 minimize해야할까? 간단하게 neural network의 output을 계산해서 expected value (target value)와 actual output value의 차이를 error로 정의하면 어떨까? 즉, neural network의 output이 우리가 원하는 output과 가장 근접한 weight를 learning하는 방법을 취하는 것이다. 근데 여기에서 문제가 하나 생기게 되는데, 바로 이 error function이 weight에 대해서 convex하지가 않다는 것이다. 당연히 관련되는 weight set도 엄청나게 많고, network자체가 convex한 form이 아니기 때문이다. 즉, 실제 좋은 performance를 내는 weight들의 여러 set을 취해 그 중간 값을 취해 얻은 weight가 좋은 weight가 아닐 수도 있다는 것이다. perceptron algorithm의 가장 attractive한 점은 algorithm이 convex하기 때문에 언제나 같은 값으로 converge한다는 점인데, 이런 방식으로는 그런 convergence가 보장이 안되는 것이다.

일단, 어쨌거나 perceptron이 적용이 안되는 상황이니깐, 위에서 정의한 error minimization의 측면에서 문제를 접근해보도록하자. 가장 간단한 예시인 Linear neuron에 대해서 살펴보자. 일단 y를 neuron을 통해서 얻어진 estimated output, w를 weight vector, x를 input vector라고 하면 다음과 같은 식을 세울 수 있다.

$$ y = \sum_i w_i x_i = \mathbf w^\top \mathbf x $$

이 상황에서 input vector x의 real output을 t (target output)이라고 해보자. 이런 상황에서 가장 간단한 error는 actual output과 desired output의 squared difference이다. 즉, 이를 수식으로 나타내면 $error = \sqrt{t-y}$로 표현할 수 있을 것이다. 우리의 목표는 이런 상황에서 weight를 iterative method를 사용하여 구하고 싶은 것이다. Iterative method라는 것은 어떤 특정한 반복적인 알고리듬을 사용하여 (예를 들어 gradient descent나 perceptron처럼) 계속 값을 update시켜나가면서 가장 적절한 것으로 보이는 값을 찾아내는 방법이다. 즉, $w_{t+1} = f(w_t) $로 표현이 가능하다. $w_t$는 t번 째 loop에서 w의 값이고, f는 w를 update하는 rule이다. 그렇다면 여기에서 잠시 궁금한 점이 생길 수 있다. 만약 우리가 target vector를 알고 있다면, 왜 문제를 analytically하게 해결하지 않을까? 즉, 우리가 이미 x와 y를 안다면 이를 가장 최적화시키는 w를 계산으로 단 한 번에 구할 수 있을 것인데, 왜 하필 iterative method를 사용하여 계속 값을 update하는 것일까? 훨씬 비효율적이지 않을까? 이 질문에 대한 알고리듬 관점에서 바라봤을 때의 답을 간략하게 말해주자면, 그런 형태의 analytic solution은 반드시 문제가 linear해야하고 또 squared error measure에 대해서만 working하기 때문인 것이 하나, 그리고 Iterative method가 조금 비효율적으로 보일지는 몰라도 더 복잡한 네트워크에 대해서 generalize하기가 더 간단힌 이유 하나를 들 수 있을 것이다.

이런 iterative method는 맨 처음 모든 weight를 random하게 guess하고 매 input마다 적절하게 weight를 update시킨다. 이 방법은 weight가 어떤 특정한 value로 converge할 때까지 계속된다. 그렇다면 이런 방법의 예를 하나 들어보자. 이 강의에서는 다음과 같은 function을 정의한다. $price = x_{fish} w_{fish} + x_{chip} w_{chip} + x_{ketchup} w_{ketchup}$ 즉, 내가 식당에서 생선과 칩과 케첩을 먹었을 때 내가 지불해야하는 금액을 내가 먹은 양 (x), 그리고 각 item들의 가격 (w)으로 나타낸 것이다. 내가 알고 있는 값은 input x (내가 시킨 양) 그리고 계산서를 통해 얻은 값이다. 하지만 나는 w를 모르며, 이 w를 찾는 것이 목적이다. 그렇다면 처음에는 random하게 w를 guess할 수 있을 것이다. 이때, (120, 50, 100)이 true weight라고 해보자. 즉, 현재 input이 2,5,3일 때 price는 850일 것이다. 현재 우리는 weight에 대한 정보가 없으므로 모두 50이라고 가정하면 내가 estimate한 price는 500이고, error의 값은 350이 된다. 이때, $\triangle w_i = \epsilon x_i (t-y)$라는 learning rule이 있다고 해보자. (이 learning rule은 delta-rule이라는 규칙으로, 바로 다음 단락에서 자세히 다루도록 하겠다.) 이 수식을 적용하면 다음 weight는 70, 100, 80이 되고 error는 30으로 줄어들게 된다 (esitimated price = 880, true = 850) 이런 식으로 각 iteration마다 error의 값을 줄여나가면서 true weight를 찾는 것이 iterative method의 작동원리인 것이다.

그렇다면 이런 방법에서 가장 중요한 개념은 아마 learning rule일 것이다. 이 렉쳐에서는 ‘Delta Rule’이라는 rule을 소개하고 있다. 이 방법은 일종의 Gradient Descent method인데, single layer neural network에서 주로 사용하는 방법이라고 한다. 자세한 설명은 wiki를 참고. 그렇다면 왜 delta-rule은 $\triangle w_i = \epsilon x_i (t-y)$ 의 꼴을 띄고 있는 것일까? 증명은 간단하다. error를 squared residuals summation error로 정의하고 차근차근 수식을 전개하면 해당 꼴을 얻을 수 있다. wiki에도 언급이 되어 있으므로 설명이 미진하다면 wiki를 참고하면 될 것 같다. 먼저 $E = \sum_j \frac 1 2 (t_j - y_j)^2$이라하자. (notation은 wiki의 notation을 사용하겠다.) 이 error는 convex function이고 domain도 convex하므로 gradient descent method를 사용하면 error의 global minimum값을 반드시 찾을 수 있다. 따라서 만약 우리가 “weight space”에 대해서 이 error를 최소화하게 된다면 매 순간 minimize하기 위해 내려가는 방향 즉, 이 함수의 gradient 값은 $\frac {\partial E} {\partial w_{ji}}$이 될 것이다. 이때, 이 gradient descent는 error를 줄이기 위해서 필요한 weight들의 change이고, 방향은 반대이므로 $\triangle w_{ij} = - \epsilon \frac \partial E \partial w_{ji}$라고 할 수 있는 것이다. 그리고 뒤의 미분항을 간단하게 chain rule을 사용하여 정리하면 이전의 식은 결국 다음과 같은 수식으로 표현이 가능하다.

$$ \triangle w_{ij} = \epsilon (t_j - y_j)x_i $$

wiki에서는 active function의 미분항까지 들어가게 되는데, 이 경우는 일단 생략하였다.

이제 update rule을 만들었으니 필연적으로 생기는 question들을 점검해보자. (1) 이 알고리듬은 반드시 global한 값으로 converge하는가? - convex optimization이기 때문에 global truth로 converge하긴한다. 적절한 step size가 필요한데 이것은 이론적으로 구할 수 있으므로 큰 상관이 없다. (2) converge rate는 얼마나 될 것인가? - gradient descent method들이 대부분 그러하듯 많이 느릴 것이다. 이를 개선하기 위해 steepest descent method를 적용하는 등의 방법이 있는 것으로 보인다. 마지막으로 perceptron과 비교해보자. perceptron은 ‘error가 발생해야만’ update가 일어났으며, error는 binary error였기 때문에 update가 일어나지 않을 수도 있었다. 하지만 지금은 error가 real function이므로 error는 거의 항상 non zero value가 되고 update도 지속적으로 일어난다. 또한 perceptron이 아무런 parameter tuning이 없던 것과 비교해 (margin은 일단 예외로 하자) learning rate를 골라야하는 귀찮은 문제가 하나 생기게 되었다.

The error surface for a linear neuron

이 소강의는 거의 언급할 내용이 없다. 앞에서 이미 이 문제가 convex임을 밝혔으며, 또한 weight space라는 concept역시 이미 언급했다. 언급되고 있는 문제는 거의 gradient descent method의 문제점들이다. 특히 convergence rate가 느린 경우, zig-zag하게 수렴하는 경우는 어떻게 해야할 것인가? 등에 대한 question만 던지는 강의이기 때문에 과감하게 생략하도록 하겠다.

Learning the weights of a logistic output neuron

delta rule을 logistic neuron에 대해 적용하는 것인데, 결론만 얘기하면

$$ \triangle w_{ij} = \epsilon (t_j - y_j) y_i (1-y_i) x_i $$

의 꼴이 된다. 즉, 앞에서 언급했던 activate function의 미분값인 $y_i (1-y_i)$가 포함되는 형태라는 것만 알아두면 된다. 다만, 이 경우에 binary threshold neuron이 아니라 logistic neuron을 쓰는 이유는 binary threshold neuron은 error가 항상 0아니면 1이기 때문에 gradient descent method를 사용할 수 없기 때문이다. 이제 간단한 배경지식을 갖추었으니 이번 렉쳐의 메인인 backpropagation으로 넘어가보자.

The backpropagation algorithm

자, 사실 앞에서 이런저런 얘기를 주절주절 했던 이유는 바로 backpropagation algorithm에 대해 설명하기 위해서였다. 이 algorithm은 당연히 iterative method이며, logistic neuron에 대해서 delta-rule (gradient descent method)를 적용하여 최적의 weight를 계산해낸다. 이 알고리듬은 hidden layer가 존재하는 neural network를 learning하기 위해 사용이 되는 알고리듬이며, 이름에서 알 수 있듯 network의 output value에서부터 역으로 weight를 learning하게 된다. 왜 우리는 hidden layer가 존재하는 neural network를 learning해야할까? 이런 방법을 쓰지 않으면 network가 항상 linear하기 때문에 real problem을 풀 수가 없기 때문이다. 그리고 또한, hidden layer를 사용한다는 의미는 우리가 임의의 feature를 정하고, 각 feature들의 weight가 얼마나 되는지 학습을 한다는 의미와 같다. 무슨 얘기이냐하면, 만약 엄청나게 dimension이 큰 input이 있을 때 (예 - 해상도 높은 사진) 실제 algorithm을 돌릴 때 모든 input을 사용해 learning하는 것은 거의 의미가 없고 (특히 high dimension, samll input인 경우는 overfitting issue가 크게 작용한다.) 해당 알고리듬에 대입해서 실행시킬 feature를 뽑아내는 과정을 필요로 하는 경우가 많다. 그런데 대부분의 경우 우리는 이런 feature를 heuristic하게 찾는다. 즉, 사진에서 눈, 코, 입을 feature로 삼아야한다고 우리의 heuristic으로 결정하고, masking을 손으로 하고 그 결과를 알고리듬에 대입하는 것이다. 그런데 hidden layer를 사용하게 되면 그런 불필요한 행동을 줄일 수 있다. 만약 hidden unit각각이 머리카락, 눈, 입술, 코, 귀 등등을 의미하고 있다면 적절한 weight를 learning함으로써 feature에 대한 weight를 결정할 수 있고, 우리가 일일이 손으로 하던 것들을 자동화시킬 수 있는 것이다. 이렇기 때문에 hidden layer가 포함된 neural network가 powerful하고 meaningful하다. 그리고 backpropagation을 사용하는 이유는 그것이 가장 효율적이고 빠른 학습 방법 중 하나이기 때문이다.

Backpropagation이 아닌 다른 예를 하나 생각해보자. 예를 들어서 output을 사용하지 않고 initial weight를 주고 weight를 조금씩 변화시키면서 적절한 값을 찾을 수도 있을 것이다. (Learning using perturbations) 즉, 원하는 target value를 고정해두고 해당 value에 가장 가깝도록 weight를 하나하나 강제로 조정하면서 전체 weight를 찾아가는 다소 reinforcement learning과 비슷한 방법으로 접근하는 것이 가능할 수도 있다. 그러나 이런 방법은 큰 문제가 있다. 먼저 weight가 많아질수록 찾아야하는 값이 많아지고 computation time이 엄청나게 빠르게 증가할 것이다. 또한 이런 방법은 weight에 대해 network가 convex하다면 의미가 있을 수 있지만 당연히 hidden layer가 포함된 network는 convex하지 않다. 결국 이 방법은 우리가 상상도 하지 못할 만큼 많은 양의 computation time을 필요로 하는 좋지 못한 방법인 것이다. 심지어 아주 적은 수의 neuron만 있더라도 바로 뒤에서 설명하게 될 backpropagation이 더 성능이 우수하기 때문에 이런 방법 자체를 사용하지 않는 것이다.

그렇다면 이제 backpropagation algorithm에 대해 discribe해보자. backpropagation의 기본 아이디어는 우리가 hidden unit들 그 자체에 대해서 알 필요가 하나도 없고 (알 수도 없을 뿐더러), 대신 hidden unit들로 인해 생성되는 error change를 관측하는 것이 더 낫다는 것이다. 즉, hidden unit 그 자체의 activity를 learning하는 것이 아니라, hidden unit들로 인해서 생겨나는 error derivatives를 사용하자는 것이다. 이 방법은 ouput layer에서 아래 layer로 정보를 backpropagation하여 (역으로 보내어) lower layer에서 그 값을 기준으로 다시 weight를 update시킨다. input pattern은 hidden layer에 전달이 되고, 다시 hidden layer가 output layer로 전달을 시키므로 (hidden layer가 하나일 때) 이런 방법으로 현재 weight에 대한 expected value와 estimated value 사이의 error를 구할 수 있고 이것을 최소화 하는 방향으로 weight를 learning하는 것이다. weight를 learning할 때는 앞에서 우리가 이미 살펴보았던 delta-rule을 사용하여 output layer에서의 각 neuron들의 error를 사용해 weight들을 update한다.

이를 그림으로 표현하면 아래와 같다. (출처: 링크)

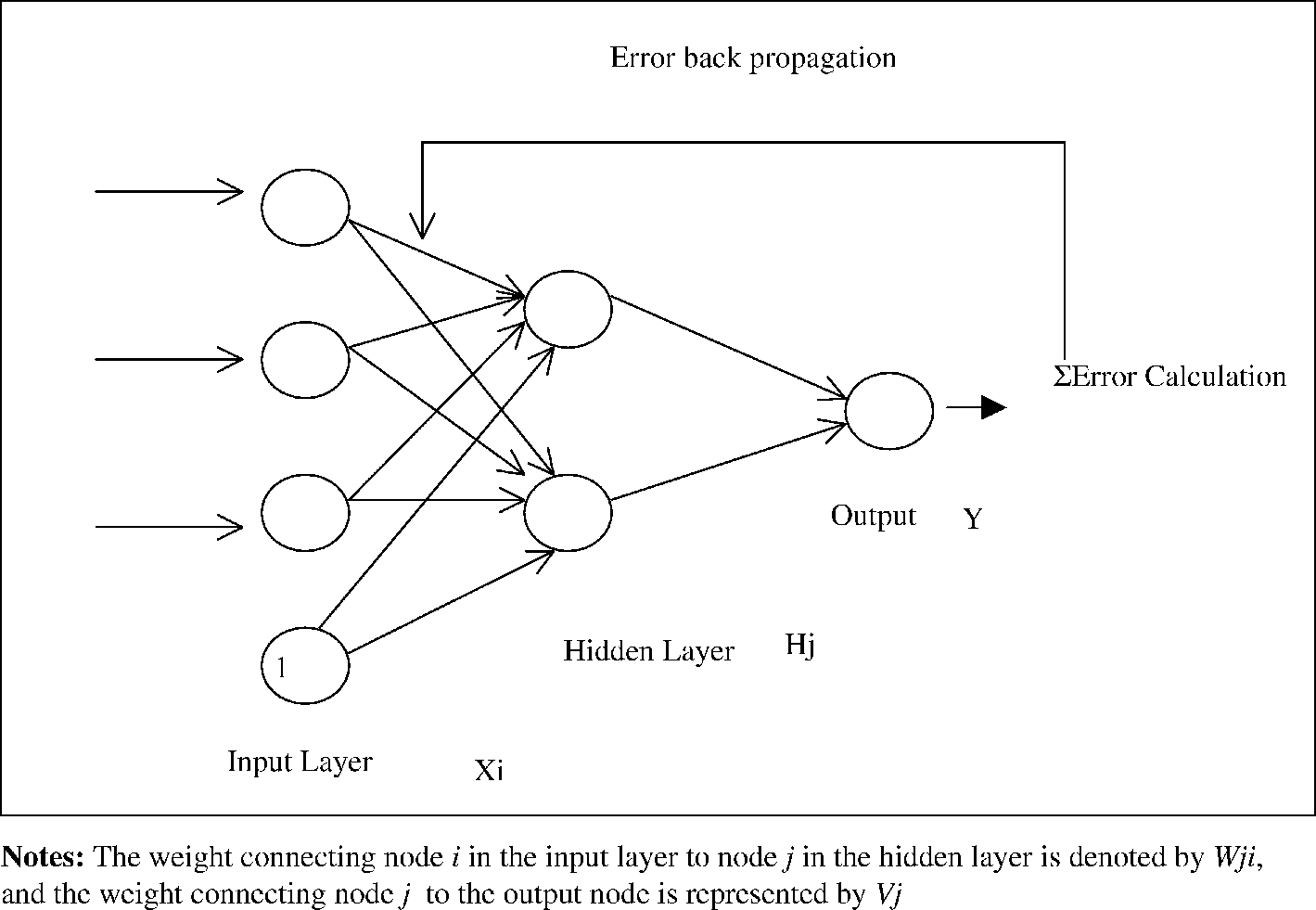
Backpropagation은 크게 두 가지 phase로 나눌 수가 있는데, 하나는 propagation phase이며, 하나는 weight update phase이다. propagation phase에서는 training input pattern에서부터 에러, 혹은 각 뉴런들의 변화량을 계산하며, weight update phase에서는 앞에서 계산한 값을 사용해 weight를 update시킨다.

Phase 1: Propagation

Forward propagation: input training data로부터 output을 계산하고, 각 ouput neuron에서의 error를 계산한다. (input -> hidden -> output 으로 정보가 흘러가므로 ‘forward’ propagation이라 한다.)
Back propagation: output neuron에서 계산된 error를 각 edge들의 weight를 사용해 바로 이전 layer의 neuron들이 얼마나 error에 영향을 미쳤는지 계산한다. (output -> hidden 으로 정보가 흘러가므로 ‘back’ propagation이라 한다.)

Phase 2: Weight update

Delta rule을 사용해 weight를 update한다. update rule은 다음과 같다. (delta rule for logistic neuron)
$ \triangle w_{ij} = \epsilon (t_j - y_j) y_i (1-y_i) x_i $

위의 과정은 output layer에서부터 하나하나 내려오면서 반복된다. 즉, output -> hidden k, hidden k -> hidden k-1, … hidden 2 -> hidden 1, hidden 1 -> input의 과정을 거치면서 계속 weight가 update되는 것이다. 그리고 이 cycle자체가 converge했다고 판단될 때 까지 계속 반복된다.

이렇듯 backpropagation은 직접 weight를 바로 변화시키는 것이 아니라 오직 error만을 보고 gradient descent method based approach를 사용해 error를 minimize하는 방향으로 계속 weight를 update시키는 것이다. 또한 한 번 error가 연산된 이후에는 output layer에서부터 그 이전 layer로 ‘역으로’ 정보가 update되기 때문에 이를 backpropagation, 한국어로는 역전사라고 하는 것이다.

How to use the derivatives computed by the backpropagation algorithm

Overfitting과 Optimization issue가 나오는데, Online, batch update 중 무엇을 고르느냐, 어떻게 overfitting을 줄이냐 등등, 이미 예전에 많이 다뤘거나 앞으로 다시 다뤄질 주제들이라 판단되어 생략하도록 하겠다.

다만, backpropagation에 대해 중요한 언급이 빠져있어서 첨언을 하자면, backpropagation 은 항상 global optimum으로 converge하지 않기 때문에 언제나 local minimum으로 converge할 가능성이 존재한다. 이는 특히 hidden layer가 많아지면, 혹은 네트워크가 deep해지면 deep해질 수록 더 심해진다. 따라서 initial value를 어떻게 설정하느냐가 매우 민감하다. initial value에 따라 수렴하는 방향이 달라질 수 있기 때문인데, 나중에 배울 Deep belif network에서는 initial value를 미리 pre-training하는 방법으로 이를 극복해낸다.

Coursera Neural Networks for Machine Learning

다른 요약글들 보기 (카테고리로 이동)

Lecture 1: Introduction
Lecture 2: The Perceptron learning procedure
Lecture 3: The backpropagation learning proccedure
Lecture 4: Learning feature vectors for words
Lecture 5: Object recognition with neural nets
Lecture 6: Optimization: How to make the learning go faster
Lecture 7: Recurrent neural networks
Lecture 8: More recurrent neural networks
Lecture 9: Ways to make neural networks generalize better
Lecture 10: Combining multiple neural networks to improve generalization
Lecture 11: Hopfield nets and Boltzmann machines
Lecture 12: Restricted Boltzmann machines (RBMs)
Lecture 13: Stacking RBMs to make Deep Belief Nets
Lecture 14: Deep neural nets with generative pre-training
Lecture 15: Modeling hierarchical structure with neural nets
Lecture 16: Recent applications of deep neural nets