들어가기 전에

이 글은 2014년 KAIST Network Science 수업 중 Graph theory 내용을요약한 글이다. 이 렉쳐에서는 가장 기초적인 Network modeling 중 하나인 random network에 대해 다룬다.

Why we need network model?

이 글을 포함해 3개의 강의는 모두 네트워크 모델링과 관련된 내용이다. 이 글은 random network, 그리고 다음 글은 순서대로 small world network, 그리고 그 다음은 scale free network에 대해 다루게 된다. 이런 네트워크 모델링을 우리는 왜 알아야할까. 사실 이유는 간단하다. 그냥 네트워크를 사용해 무언가를 분석하는 것이 매우 어렵기 때문이다. 예를 들어서 우리는 실제 social network가 어떻게 구성되어있는지 알지못한다. 만약 우리가 실제 네트워크와 매우 유사한, 그러나 훨씬 간단한 형태의 모델을 만들게 된다면 해당 네트워크에서 발생하게 될 일들을 쉽게 예측할 수 있을 것이다. 이 글에서 다루게 되는 random network는 그러한 네트워크 모델링 중에서 가장 간단한 모델 중 하나이다.

Random Graph

Random graph란 어떤 fixed parameter를 가지는 stochastic 모델이다. Notation은 $G(n,p)$ 로 적게 되는데, n은 vertex의 개수, p는 각각의 vertex pair들이 서로 edge를 가질 independent probability를 의미한다. 즉, 이 network는 확률 p로 인해 edge가 생성되므로 매번 새로 generate할 때 마다 그 결과가 달라지는 stochastic model인 것이다. 따라서 우리가 n개의 vertex와 m개의 edge를 가지는 임의의 network $G(n,m) $를 얻게 될 확률은 $P(G) = p^m (1-p) ^ { {n \choose 2} - m} $ 로 얻을 수 있다. 이러한 모델을 맨 처음 수학적으로 이를 분석했던 사람들의 이름을 따서 Erdös-Rényi model 이라고도 하고 그 degree와 edge의 distribution이 Poisson혹은 Bernoulli 분포를 따르기 때문에 Poisson random graph 혹은 Bernoulli random graph라고 하기도 한다.

Mean Edge and Mean Degree in Random Graph

아런 Random graph에서 n과 p가 주어졌을 때, graph가 generate가 될 때마다 항상 edge의 개수는 달라지지만, 이것이 특정 확률을 따르기 때문에 평균 edge의 개수를 계산하는 것이 가능하다. 계산하기 전에 간단하게 생각하면 n개의 vertex에 존재하는 모든 pair들 중 확률 p로 edge를 가지기 때문에 평균 edge의 개수는 모든 pair의 개수에서 edge가 존재할 확률인 p를 곱한 $ {n \choose k} p$ 가 될 것이다. 그렇다면 정말 그런지 확인해보도록 하자. 그러면 먼저 m개의 edge를 가지는 임의의 Graph $G(m)$ 이 generate될 확률을 구해보자. 이 갚은 바로 위에서 edge가 m개인 graph $G(m)$ 하나가 표현될 확률을 계산했으므로, 이런 graph의 개수를 count한 후 간단하게 이를 summation하면된다.

$$ P(m) = { {n \choose 2} \choose m} p^m (1-p)^{ {n \choose 2} - m} $$

위에서 우리는 m에 대한 확률 분포를 구했기 때문에 m의 평균 값은 간단하게 $\sum_m mP(m)$ 으로 계산할 수 있다. 그런데 $m$의 확률 분호 $P(m)$은 $n$이 ${n \choose m}$ 이고 $k$가 $m$인 binomial distribution이다. 또한 우리는 binomial distribution의 mean value가 단순하게 $np$ 임을 알고 있으므로 평균 값은 아래와 같이 계산할 수 있다. 이에 대한 자세한 설명은 위키피디아 링크로 대체한다.

$$ \bar m = \sum_{m=0}^{n \choose 2} m P(m) = {n \choose 2} p $$

이 결과는 우리가 처음 예측한 값과 정확히 일치한다.

그러면 이제 degree의 평균 값을 구해보자. 그 이전에 이번에는 mean degree가 얼마일지 간단하게 생각해보자. 이때 mean degree라는 것은 결국 한 vertex에서 가지는 평균 edge의 개수를 의미하기 때문에 평균 edge개수인 ${n \choose k}p$를 vertex pair 개수인 $n \over 2$로 나눠준 값인 $(n-1)p$ 가 될 것이라고 예측할 수 있다. 그렇다면 실제로 계산해보자. 이전 글에서 이미 우리가 유도했던 것처럼 edge가 $m$개 있는 graph의 mean degree는 $2m \over n$으로 구할 수 있다. 따라서 평균 degree는 위에서 우리가 edge의 평균 개수를 구한 것 처럼 간단히 구할 수 있다.

$$ \bar k = \sum_{m=0}^{n \choose k} {2m \over n} P(m) = {2 \over n} {n \choose 2} p = (n-1)p $$

역시 처음에 예측한 값과 일치한다. 참고로 random graph에서 평균 degree는 $c$라는 notation으로 표기가 되며, 따라서 $c=(n-1)p$이다.

Degree Distribution

그렇다면 이번에는 degree의 distribution을 알아보자. 평균 degree의 개수도 물론 중요하지만 실제 degree가 어떻게 분포하고 있는지를 아는 것도 매우 중요하다. 왜냐하면 결국 network의 특성을 이해하기 위해서는 개별 node들이 얼만큼 다른 node들과 연결되어있는지 알아야하며, 이 결과가 네트워크에 어떤 결과를 불러올지 파악하는 것이 매우 중요하기 때문이다. 그렇다면 먼저 간단하게 하나의 vertex가 $k$개의 다른 vertex와 연결되어있는 상황이 발생할 확률을 계산해보자. 이때, 당연히 전체 vertex 개수는 $n$개 이므로 $k$개의 vertex와 연결되어있는 vertex는 나머지 $n-1-k$ vertex와 연결되어있지 않다. 따라서 임의의 vertex가 $k$개의 vertex와 연결되어있을 확률 $p_k$는 아래와 같이 계산된다.

$$ p_k = { n-1 \choose k } p^k (1-p)^{n-1-k} $$

이 결과는 또 binomial distribution이다. 즉, $G(n,p)$의 degree distribution은 binomial distribution이라는 것을 알 수 있다. 하지만 이 식은 간단한 근사식을 통해서 더 간단하게 표현하는 것이 가능하다. 대부분의 경우 우리가 관심이 있는 영역은 $n$이 엄청나게 큰 network이므로 이런 상황에서 앞 부분의 combination을 근사하고, 그 다음에는 뒷 부분의 $(1-p)^{n-1-k}$의 log 값을 근사 시켜보자.

먼저 $n-1 \choose k$를 근사한 결과는 ${n-1 \choose k} = {(n-1)! \over (n-1-k)! k!} \simeq {(n-1)^k \over k!}$ 이다. 이 근사식은 그냥 매우 간단한 근사식이므로 설명을 생략하도록 하겠다. 그렇다면 이제 다음으로 확률의 맨 뒷부분을 근사해보자. 이 값은 먼저 log를 취한 후 log를 근사하여 그 값을 계산한다.

$$ \ln[(1-p)^{n-1-k}] = (n-1-k) \ln ( 1- \frac {c} {n-1}) \simeq -(n-1-k) { c \over n-1} \simeq -c $$

이 근사식에서 첫 번째 계산식은 $p = { c \over n-1} $이라는 이전의 결과를 사용한 것이고 근사하는 부분은 log의 taylor expansion이 $\ln(x) = (x-1) - {(x-1)^2 \over 2} + {(x-1)^3 \over 3} - …$ 라는 것을 사용한 것이다. 그 다음 근사는 당연히 n이 k보다 엄청 크다고 가정한 것이다. 자 그 결과는 놀랍게도 $\ln[(1-p)^{n-1-k}] \simeq -c$ 이다. 즉, $(1-p)^{n-1-k} \simeq e^{-c}$ 라는 사실을 알 수 있다.

자 이제 모든 결과를 종합해보면 n이 엄청나게 큰 상황에서 다음과 같은 결과를 얻는다

$$ p_k \simeq {(n-1)^k \over k!} p^k e^{-c} ={ (n-1)^k \over k!} ({c \over n-1})^k e^{-c} \simeq e^{-c} {c^k \over k!}$$

자, 우리는 n이 매우 크다는 조건 하나를 사용해 근사를 한 결과 Poisson distribution을 얻게 되었다. 즉, n이 매우 큰 $G(n,p)$에서 degree distribution은 poisson distribution을 가진다는 사실을 알 수 있다. (사실 글의 처음에서도 말했던 것 처럼 이런 이유로 random network라는 이름은 사실 poisson random graph의 준말이다.)

Cluster and giant Component

자 그러면 이제 또 중요한 measurement 중 하나인 clustering coefficient를 계산해보자. Random Graph에서 $c$는 평균 degree를 의미하기 때문에 이 글에서 clustering coefficient는 $C$로 표기될 것이다. 이 clustering coefficent는 내가 이웃한 vertex 두 개가 서로 연결되어있을 확률을 의미한다. 그런데 우리의 graph $G(n,p)$의 임의의 vertex pair가 서로 연결되어있을 확률은 언제나 $c \over n-1 $이다. 따라서 clustering coefficient $C$는 $c \over n-1 $ 라는 사실을 아주 간단하게 알 수 있다. 즉, 이 식에 따르면 $n \to \infty$ 가 되고 $c$의 값이 fixed 되어있는 graph에서의 $C$는 0으로 수렴한다는 사실을 알 수 있다. 그러나 실제 네트워크에서 관찰되는 결과는 mean degree가 fixed되어있더라도 clustering coeficient의 값이 여전히 크게 유지가 된다는 것이다. 이런 특성 때문에 바로 다음 글에서 설명하게 될 small world network의 필요성이 대두된다.

아무튼 단순히 clustering coefficient만 계산하는 것은 크게 와닿지 않는다. 구체적으로 이 네트워크에서 giant component라는 것이 존재할 확률이나 실제 존재했을 때 어떤 형태로 존재할지를 예측해보자. 여기에서 giant component란 문자 그대로 네트워크 상에서 존재하는 가장 largest한 component라고 보면 된다. (Component에 대한 설명은 이전 글 참고) Simple하게 $p=0$이면 모든 graph가 disjoint되어있고 giant component라는 것은 존재하지 않는다. 반면 $p=1$이면 모든 vertex가 연결되어있고 graph는 vertex의 개수가 $n$인 오직 하나의 componet를 가지게 된다. 자 그러면 이제 $p$가 0에서 1사이의 값일 때를 생각해보자. 이런 상황에서 giant component가 존재한다고 가정하고, 이 component에 포함되는 vertex의 개수를 $n_{gc}$ 라고 하자. 이렇다고 가정을 하게 되면 임의의 fraction of nodes가 giant component에 포함이 되지 않을 확률을 $u$라고 하면 우리는 이 값이 $u=1-{n_{gc} \over n}$ 이라는 사실을 알 수 있다. (당연히 $n_{gc} = n(1-u)$ 이다.) 그렇다면 이제 이 u를 통해 giant component를 분석해보도록 하자.

먼저 임의의 vertex $i$가 이런 GC에 포함된다고 가정해보자. 그렇다면 이 vertex $i$는 vertex $j$라는 vertex를 거쳐 GC에 연결되어야한다고 했을 때, $i$가 GC에 포함이 되지 않을 확률은 (1) $i$와 $j$가 연결되어있지 않다: $1-p$ (2) $i$와 $j$가 연결되어있으나 $j$가 GC에 연결되어있지 않다: $pu$ 이렇게 총 두 가지 경우 임을 알 수 있다. 따라서 임의의 vertex $i$가 임의의 다른 vertex $j$를 거쳐 GC에 포함되지 않을 확률은 $1-p+pu$이고, 다른 모든 vertex에 대해 이를 확장해보면 다른 vertex가 $n-1$개 있으므로 이 확률은 ${(1-p+pu)}^{n-1}$ 임을 알 수 있다. 그런데 이 값은 결국 한 vertex가 GC에 포함될 확률 $u$와 같다. 따라서 $u={(1-p+pu)}^{n-1}$ 이라는 사실을 알 수 있다.

자, 그러면 $p={c \over n-1}$ 이므로 위의 식에 대입하고, log를 근사시키면 아래와 같은 결과를 얻게 된다.

$$ \ln u= (n-1) \ln {\left(1-{c \over n-1} (1-u) \right)} \simeq -(n-1) {c \over n-1} (1-u) = -c (1-u) $$

위의 식을 통해 $u=e^{-c(1-u)}$ 라는 사실을 알 수 있다. 이때 giant component 안에 들어있는 vertex의 개수의 비율을 $S=1-u={n_{gc} \over n}$ 이라고 정의한다면 이 식은 아래와 같이 적을 수 있다.

$$ S=1-e^{-cS} $$

이로부터 우리는 Giant component의 크기 자체가 평균 degree에 의해 bound된다는 사실을 알 수 있다. 즉, 어떤 값 $c$에 의해 S가 결정된다는 것이다. 그러나 식이 한 번에 풀릴 수 있는 간단한 형태가 아니기 때문에 이 식에서 바로 정확한 S값을 구할 수는 없고, 그 대안으로 graphical solution이 제시된다. 즉, x축이 S의 값이고 y축이 S에 대한 함수의 값인 2차원 그래프를 그리고, $y=S$와 $y=1-e^{-cS}$의 교점을 구하는 것이다. 이런 두 함수를 그려보게 되면 아래와 같은 결과를 얻게 된다.

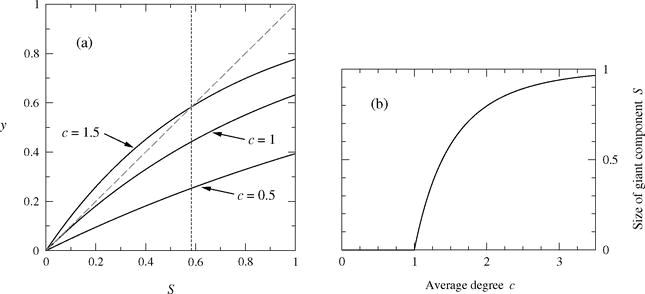
위의 그래프에서 알 수 있는 사실은, 모든 함수들이 원점에서부터 시작하고 계속 기울기가 감소하는 형태이기 때문에 만약 원점에서 함수의 기울기가 1보다 큰 값이 존재하는 함수가 존재한다면 그 함수는 반드시 원점이 아닌 교점이 존재한다는 사실이다. 이런 교점을 찾아보면, ${d \over dS} (1-e^-{-cS})=1$이라는 식을 풀어야하며 이 식을 계산해보면 $ce^{-cS} = 1$이라는 식을 얻을 수 있다. 즉, S=0인 점에서 기울기는 무조건 $c$가 되므로 $c$의 값이 1보다 크면 반드시 giant component가 존재하며 그 보다 작으면 giant component가 존재하지 않는 다는 것을 알 수 있다.

Small Componets

이번에는 Giant component에 포함되어있지 않은 Small component에 대해 알아보자. 만약 giant component가 네트워크에 딱 하나만 존재한다고 가정해보자. 그리고 각각의 크기가 $S_1 n$ $S_2 n$ 이라고 가정했을 때, $i$가 첫 번째 GC에 속하는 vertex, $j$가 두 번째 GC에 속하는 vertex일 때, 모든 distinct vertex pair $(i,j)$의 개수는 간단하게 그 둘을 곱한 $S_1 S_2 n^2$일 것이다. 만약 각각의 pair는 $p$의 확률로 연결이 되어있거나 $1-p$의 확률로 연결되어져있지 않다. 따라서 이 두 개의 GC가 서로 완벽하게 분리되어있을 확률 $q$는 다음과 같이 계산할 수 있다

$$ q = (1-p)^{S_1 S_2 n^2} = \left( 1 - {c \over n-1} \right)^{S_1 S_2 n^2} $$

이때 만약 $n \to \infty$ 가 된다면, 우리는 아래와 같은 근사식을 구할 수 있다.

$$ \ln q = S_1 S_2 \lim_{n \to \infty} \left[ n^2 \ln \left( 1 - {c \over n-1} \right) \right] = S_1 S_2 \left[ -c(n+1) + {1 \over 2} c^2 \right] = c S_1 S_2 [-n + ({1 \over 2} c -1) ]$$

그러면 우리는 남은 상수항을 $q_0$라 정의하고, $q = q_0 e^{-c S_1 S_2 n}$ 이라는 식을 구할 수 있다. 이 식은 너무나 당연하게 $n \to \infty$ 가 되면 값이 0이된다. 따라서 우리는 $n$이 매우 큰 상황에서 두 개의 GC가 존재할 확률이 0이므로 $n$이 큰 네트워크는 단 하나의 Giant component를 가지고 있다는 결론을 내릴 수 있다.

Random network는 단 하나의 Giant component만을 가지고 있기 때문에, 그에 포함되지 않은 나머지 component들을 모두 small component라고 정의할 수 있을 것이다. 이 때 각각의 small component의 크기를 $\pi_s$라고 정의하면 이 값들의 모든 합은 반드시 $1-S$이므로 $\sum_s \pi_s = 1-S$ 라는 식을 얻을 수 있다.

본격적으로 small component에 대해 다루기 전에 먼저 small component가 어떤 형태로 구성이 되어있을지 생각해보도록 하자. 정답부터 말하자면, small component는 tree의 형태를 하고 있다. 각각의 small component를 $s$개의 vertex를 가지는 tree라고 해보자. 당연히 tree의 edge의 개수는 $s-1$일 것이며 이 값은 connected 되어있는 $s$의 vertex가 만들어낼 수 edge의 최소 개수이다. 만약 이 최소 개수보다 많은 edge가 단 하나라도 존재할 확률은 $c \over n-1$이며, 이런 graph는 반드시 cycle이 생기게 되므로 더 이상 tree가 아니게 되어버린다. 그렇다면 우리가 이 small component가 tree임을 입증하기 위해서는 이런 additional edge가 존재할 확률이 0라는 것을 보이면 된다. tree를 구성하는 edge이외에 추가가 될 수 있는 edge의 개수는 ${s \choose 2} - (s-1) = {1 \over 2} (s-1)(s-2)$이다. 이를 통해 tree안에 이런 edge가 단 하나라도 존재할 확률은 ${1 \over 2} {c(s-1)(s-2) \over n-1}$ 라는 것을 알 수 있다. 따라서 $n \to \infty$ 가 되면 이 확률은 0이 되어버린다. 따라서 이 component는 반드시 tree라는 사실을 알 수 있다.

이번에는 아래와 같은 상황을 한 번 상상해보자. 왼쪽과 오른쪽은 단 하나의 vertex만 제외하면 완벽하게 같은 Graph이다. 왼쪽 graph는 vertex $i$의 neighbor들이 모두 다른 small component에 속해있는 경우이며, 즉, 서로 분리되어있는 subgraph들을 하나로 이어주는 역할을 하고 있다. 오른쪽은 그 $i$는 없지만 여전히 서로 같은 확률을 그대로 유지하고 있고 여전히 확률 p를 가지는 random graph 이다.

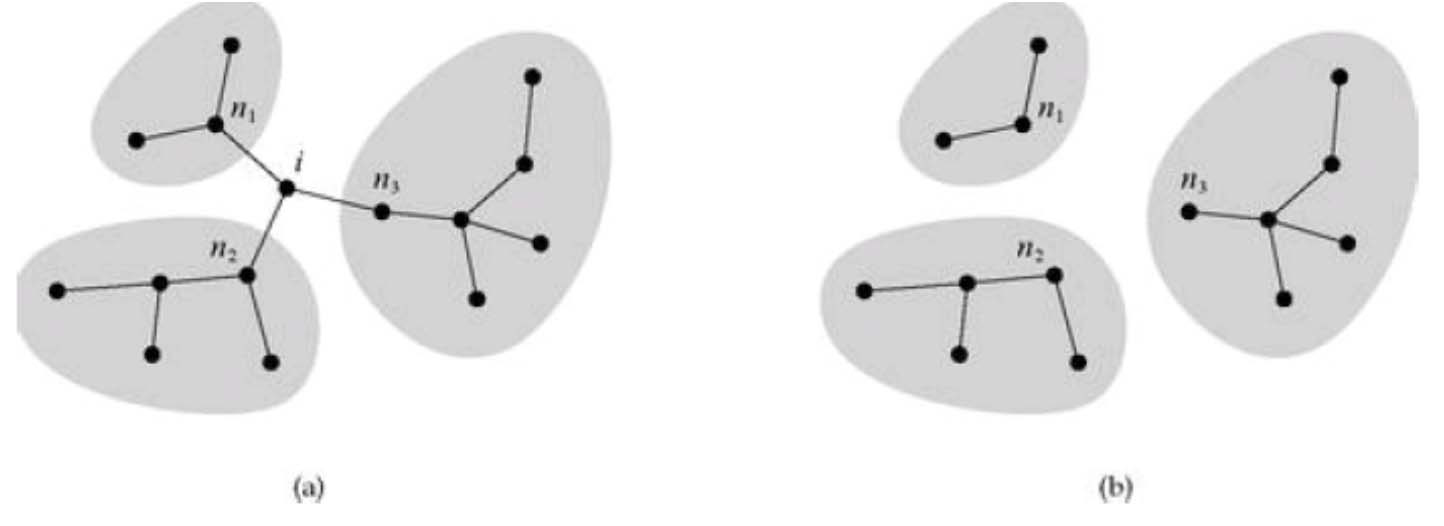
이런 상황에서 만약 우리가 충분히 큰 $n$을 가정했을 때 각각의 subgraph 역시 큰 graph의 특성을 따라갈 것이기 때문에, $i$가 없는 오른쪽 그림에서$i$의 neighbor $n_1$이 size가 $s_1$인 small component에 속할 확률은 $\pi_{s_1}$로 주어진다는 것을 예측할 수 있다.

자 그렇다면 이런 vertex $i$가 $k$의 degree를 가지고 있었다고 가정해보자. 위의 결과로 인해 vertex $i$가 $s$ 만큼의 크기를 갖는 small component에 속할 확률 $P(s|k)$는 이 vertex의 모든 neighbor, 즉 $k$개의 neighbor들이 각각 $s_1$부터 $s_k$까지 속할 확률과 같으며 이 값은 아래와 같이 계산 할 수 있을 것이다.

$$ P(S|k) = \sum_{s_1}^infty … \sum_{s_k}^{\infty} \left[ \Pi_{j=1}^k pi_{s_j} \right] \delta (s-1, \sum_j s_j) $$

이때 $\delta (m,n)$은 Kronecker delta를 의미하며 이 함수는 간단하게 두 값이 같으면 1 다르면 0을 반환한다. 즉, 이 수식에서 델타의 의미는 모든 $s_j$들을 더하면 $s-1$이 나와야한다는 것이다. =========== 추가 설명 작성 중 =============

============Small component에 대한 추가 설명 작성 중=================

Complete Distribution of Component Size

Path Length

보통 네트워크, 혹은 그래프에서 Diameter, 혹은 지름이라 함은 가장 긴 longest geodesic distance를 의미한다. 이 값은 즉, 임의의 두 vertex를 골랐을 때 가장 짧은 경로의 길이를 의미한다고 보면 된다. Random graph에서 이 값은 어떻게 구할 수 있을까? 먼저 간단하게 임의의 vertex에서 $s$ 번 이동했을 때 visit할 수 있는 평균 vertex의 개수는 매 진행마다 degree 만큼의 vertex를 추가로 더 갈 수 있으므로 평균 degree들을 $s$번 곱한 형태인 $c^s$일 것이다. 그리고 우리가 원하는 경로는 가장 짧은 경로를 찾는 것이므로 vertex travel step을 이 visit 가능한 vertex와 전체 vertex의 개수가 같아지는 순간 끝나하면 우리가 원하는 shortest path의 길이를 유추할 수 있게 될 것이다. (정확한 경로는 예측할 수 없지만) 따라서 $c^s \simeq n$이 될 것이며 따라서 $s \simeq {\ln n \over \ln c}$가 될 것이다. 즉, 놀랍게도 아무리 $n$의 값이 급격하게 커지더라도 random graph의 diameter가 증가하는 속도는 $\log n$ 이라는 것이다. 이 값은 충분히 작은 값으로, 이런 움직임이 실제 네트워크의 움직임과 매우 흡사하다는 것을 실험을 통해서 밝혀졌다.

Random Graph의 문제점

앞서 살펴본 바를 토대로 Random Graph가 가지고 있는 문제점들을 살펴보도록 하자. 먼저 Average path length는 $\bar l \simeq {\log n \over \log c} $로 표현이 되며 이것은 곧, random graph는 $n$의 값에 비례하여 path length가 늘어나는 것이 아니라 log scale로 증가한다는 것을 알 수 있다. 즉, $n$이 매우 크더라도 path는 그에 비해 매우 짧다는 것을 알 수 있다. 이것은 실제 대부분의 네트워크들에서도 나타나는 현상이다. 반면 clustering coefficient는 $c \over n$으로 표현이 되며 $n$의 값이 증가할 수록 떨어지는 것을 알 수 있는데, 실제 network들이 $n$이 커지더라도 높은 clustering coefficient를 유지한다는 점에서 현실과 잘 맞지 않는다는 것을 알 수 있다. 마지막으로 Degree distribution을 살펴보게 되면, random graph에서의 degree distribution은 $P(k) \simeq e^{-c} {c^k \over k!}$로 근사가 되는데, 실제 네트워크에서 관측되는 distribution은 $P(k) \simeq k^{-\gamma}$ 와 같은 power distribution이다. 따라서 이 역시 잘 맞지 않는다는 것을 알 수 있다.

Random network는 가장 간단한 network모델이며 수학적으로 잘 증명되었고 쉽게 이해할 수 있는 network모델이다. 그러나 real network와 비교해 잘 맞지 않는 점들이 있기 때문에 우리는 결국 새로운 network model들을 계속 더 공부해야만 하는 것이다.

따라서 다음 글은 이와 같은 문제를 일부 해결한 Small world network에 대해 다루게 될 것이다.

KAIST Network Science

다른 요약글들 보기 (카테고리로 이동)

• Lecture 1: Introduction
• Lecture 2: Graph Theory
• Lecture 3: Measures and Metric
• Lecture 4: Random Network
• Lecture 5: Small world Network
• Lecture 6: Scale free Network