README   SanghyukChun's Blog

Network Science - Small World Network (Watts-Strogztz Network)

| Comments

들어가기 전에

이 글은 2014년 KAIST Network Science 수업 중 Small World Network 내용을 요약한 글이다. 이 렉쳐에서는 Small World Network라는 concept과 실제 그런 컨셉을 적용한 Network model 중 하나인 Watts-Strogztz Network에 대해 다루게 된다.

Prolem of Random Network

이전 글에서 다뤘 듯, Random Network는 실제 Network와 맞지 않는 부분이 많이 존재한다. 가장 큰 문제는 degree distribution과 clustering coefficient가 실제 network 분포와 크게 반하다는 점이다. 따라서 이 글에서는 그런 점들을 개선시킨 새로운 컨셉의 네트워크 모델링에 대해서 다루게 될 것이다. 사실 이 Small world network라는 것이 맨 처음 1998년도 논문으로 발표가 되었을 때 그 기반이 되는 Network가 Regular Network이기 때문에 이런 Regular Network에 대해서도 다룬 이후에 Small World Network를 다루는 것이 맞다고 생각하지만, 실제 강의 내용에서 Regular Network 생략되었기 때문에 나 역시 이 글에서 Regular Network에 대해서는 많이 다루지 않을 생각이다. 참고로 Regular Network는 모든 vertex가 같은 degree를 가지는 Network를 의미하며 k-regular network라고 하면 모든 vertex의 mean degree가 $k$라는 의미이다. 그런데 이 lecture에서는 local degree의 값이 $k$가 아니라 $2k$이며 $k= {m \over n}$으로 정의한다. 엄청나게 헷갈리기는 하지만.. 일단 lecture의 notation을 따르도록 하겠다. 즉, 2-regular network는 local degree가 4이며 즉, 각 vertex는 4개의 edge를 가진다. 실제 이 chapter 자체가 2-regular network를 small world network로 바꾸는 Watts-Strogztz Network에 대한 내용이므로 이 점을 꼭 숙지하고 넘어가야한다.

Small World Network

Small world network란 예전 인터넷 속의 수학에서도 간략하게 다뤘던 내용이므로 예전 글을 참고해도 좋을 것 같다. Small World Network란 높은 clustering coefficient를 가지고 있고, 상대적으로 짧은 diameter를 가지고 있으며 entropy가 scalable한 sparse network를 의미한다. 여기에서 여러 가지 용어들이 나오는데, clustering coefficient는 넘어가도 되고, diameter는 network에서 가장 긴 shortest path, 그리고 entrophy는 이 graph를 나타내기 위한 information의 양을 의미한다. 마지막으로 sparse network라는 것은 모든 vertex pair사이에 edge가 존재하는 것이 아니라 edge가 존재하지 않는 vertex pair가 존재한다는 의미이다. Small world network는 regular network와 random network의 중간 정도 쯤 되는 network인데, 역시 이것도 이전 글에서 다뤘던 내용이므로 관심이 있다면 간략하게 읽어보기를 권한다. 간단하게 설명하면 Samll world network는 regular network에 적당한 randomness를 추가하여 얻을 수 있기 때문에 이 두 개의 네트워크의 중간 정도라고 표현하는 것이다.

사실 이 Small world라는 단어는 Stanley Milgram의 6 degree 실험에서 처음 등장한 것인데, 이 실험에 대한 자세한 설명은 이전에 적은 글을 참고하기를 바란다. 이 실험의 결론만 얘기하자면 실제 social 네트워크에서는 임의의 vertex pair를 선택했을 때 그 둘 사이를 지르는 가장 짧은 path의 길이가 network의 크기에 비해서 엄청나게 짧다는 것이다. 이 실험에서는 실제 미국 내의 네트워크에서 6개의 step이면 상대방에게 도달할 수 있다는 것을 알 수 있었다. (심지어 shortest path도 아니고 greedy search 였음에도 불구하고) 이 글에서 설명하게 될 Small world network 역시 상대적으로 짧은 diameter를 가지게 되고, clustering coefficient와 closeness centrality도 높다.

Watts-Strogatz Procedure

그러면 이제 small world network를 generate하는 방법에 대해 생각해보자. 이 과정을 Watts-Strogatz Procedure라고 부른다. 이 algorithm은 k-regular network를 small world network로 만드는 알고리듬인데, 주어진 k-regular network의 임의의 $pm$ 개의 edge를 random하게 rewire를 시킴으로써 얻을 수 있다. 즉, 내가 임의로 regualr network에서 p의 확률로 하나의 edge를 random 한 edge로 바꿔주는 과정을 계속 반복하기만 하면 된다. 이런 과정을 통해 우리는 regular network에 강제적으로 randomness를 주입할 수 있게 되며, $p$가 약 1~4% 정도가 되면 small-world effect가 나타난다고 한다. 이 $p$의 값 0.01 ~ 0.04를 transition threshold 혹은 crossover point라고 한다.

놀라운 사실은, 이렇게 간단한 algorithm을 적용하기만 해도 degree sequence distribution, diameter, average path length 등의 정보가 크게 달라지게 된다. 특히 diameter와 average path length는 아주 조금의 randomness만 주입하게 되어도 그 값이 크게 감소하게 되는데, 이런 극적인 거리 감소 현상을 곧 small-world effect라고 하는 것이다.

이런 과정을 통해 얻어지는 Small world network는 아래 그림과 같다. 이 그림은 vertex가 20개 있는 2-regular network를 WS procedure를 사용해 reconstruct한 것으로, p의 값이 점점 올라가면서 그 모양이 바뀌는 모습을 관측한 것이다.

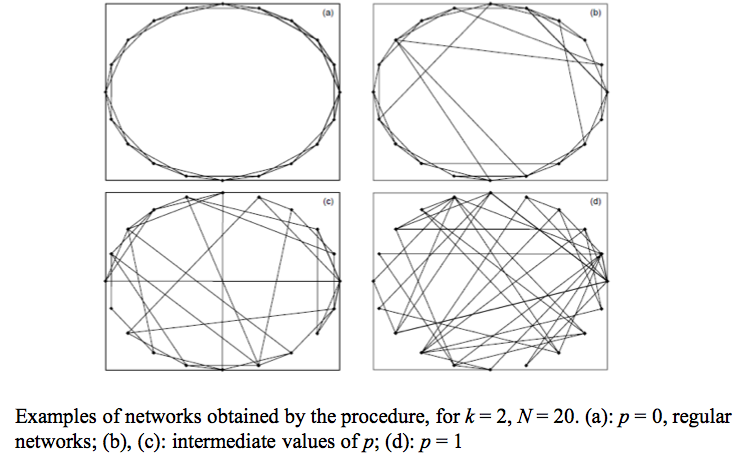
자 그런데 지금까지 설명한 방법은 완전히 random procedure이기 때문에 connected graph를 보장할 수 없다. 어떻게 이것을 개선시킬 수 있을까? 간단하게 생각할 수 있는 방법으로는 만약 선택한 edge를 제거했을 때 isolated vertex가 생기는 경우 해당 edge를 바꾸지 않도록 하는 방법이 있을 수 있을 것이다. 2000년도 뉴먼이 제시한 NSWS model에서는 이런 문제를 해결한 새로운 알고리듬을 제시했다고 하는데 논문은 찾은 것 같은데 자세히 읽어보지는 못했다.

Degree Sequence Distribution

Degree Sequence는 Graph $G$의 모든 $n$ vertex들의 degree value 들의 sequence이며 $g=[d_1, d_2, d_3, …, d_n ]$ 과 같이 표현된다. 그리고 이것의 distribution, 즉, degree가 1인 node 들의 비율, 2인 node들의 비율.. 등등을 표현하는 distribution은 $g’ = [h_1, h_2, h_3, … h_{max_d}]$ 라고 표현할 수 있다.

맨 처음 k-regular network의 모든 vertex들이 가지는 edge의 개수는 $2k$이다. 그런데 $p$의 확률로 edge가 변경되더라도 결국 평균 edge의 개수, 혹은 connectivity는 $c=2k$로 고정될 것이라는 사실을 알 수 있다. 자 이제 $P_p (c)$를 degree의 probability distribution이라고 해보자. vertex들의 2k connection 중 k개의 connection은 아직 still untouched 일 것이므로, 이런 상황에서 vertex i의 connectivity는 $c_i = k+n_i \ n_i \geq 0 $라는 것을 알 수 있다. 이제 $n_i $라는 것도 두 가지 부분으로 나눠 생각할 수 있는데, 먼저 $n_i^1 \leq k $ 은 $1-p$의 확률로 rewire되지 않는 link e들의 개수이고, $n_i^2 = n_i - n_i^1$ 은 그 반대로 vertex $i$에 reconnected된 edge들을 의미한다. 그리고 총 $N$개의 vertex가 있다고 했을 때, 임의의 edge가 vertex $i$로 rewire될 확률은 $p \over N $라는 것도 알 수 있다.

그렇다면 우리는 이 사실을 통해 small world network의 degree sequence distribution을 다음과 같은 과정을 통해 얻을 수 있게 된다.

$$ P_1 (n_i^1) = {k \choose n_i^1} (1-p)^{n_i^1} p^{k-n_i^1} $$

$$ P_2 (n_i^2) = {(kp)^{n_i^2} \over n_i^2 !} e^{-pk} \ for \ large \ N $$

$$ P_p (c) = \sum_{n=0}^{min(c-k, k)} {k \choose n} (1-p)^n p^{k-n} {(kp)^{c-k-n} \over (c-k-n)!} e^{-pk} \ c \geq k $$

아래 그림은 degree sequence distribution $P_p (c)$를 connectivity $c=2k$에 대해 표현한 것이다.

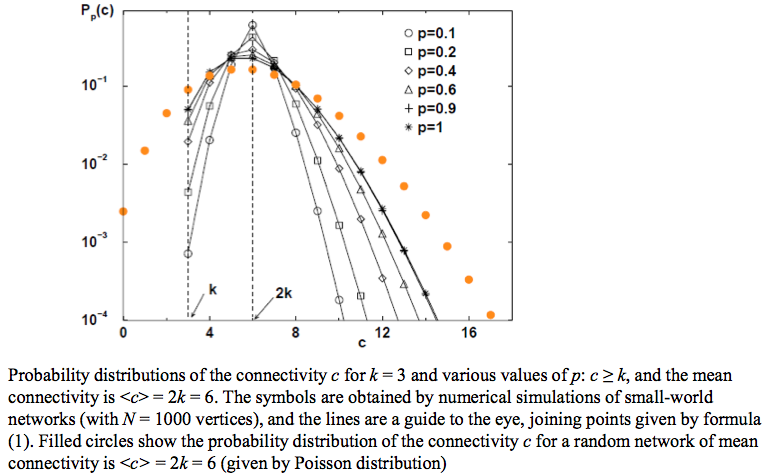
이 그림을 통해 우리는 degree sequence distribution이 평균값이 $\bar c = 2k$인 Poisson 분포임을 알 수 있다.

이번에는 random network와 실제 network data, 그리고 앞서 서명한 과정을 사용해 만들어낸 network의 degree distribution을 비교한 그림을 살펴보자

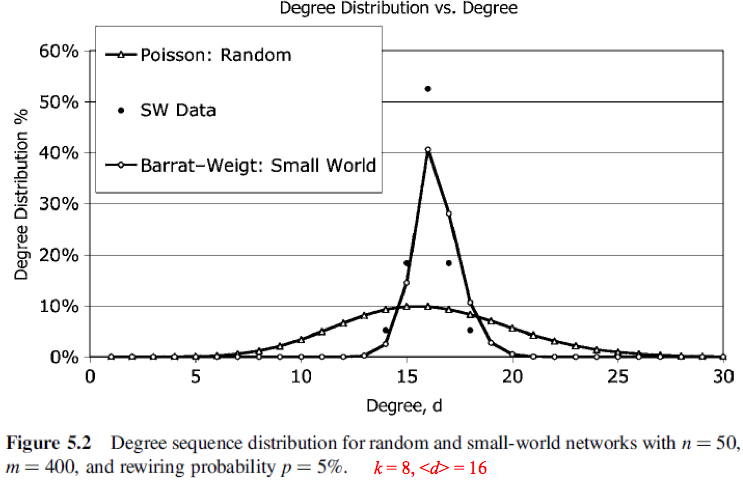
이 그림을 통해 우리는 random network보다 small world network가 더 실제 네트워크와 더 비슷하다는 것을 알 수 있다.

Entropy

앞서 정의했었던 Degree sequence distribution을 사용하면 Graph의 entropy $I(G)$를 정의할 수 있는데 이 값은 곧 네트워크를 표현 하기 위한 information의 양을 의미한다. 당연히 Regular Network는 Entropy가 낮고 Random Network는 Entropy가 높다. 다시 말해서 Graph $G$의 Entropy는 그 graph의 randomness를 bit로 표현한 값이 되며, 이 randomness는 다시 말해서 degree sequence $g’$으로 다음과 같이 나타낼 수 있다.

$$ I(G) = - \sum_{i=1}^{max_d} h_i (\log_2 h_i), \ where \ g’ = [h_1, h_2, h_3, … h_{max_d}] $$

이 값을 확률 2-regular network를 $p$의 확률로 edge를 rewire하는 경우에 대해 ploting을 해보면 다음과 같은 결과를 얻을 수 있다.

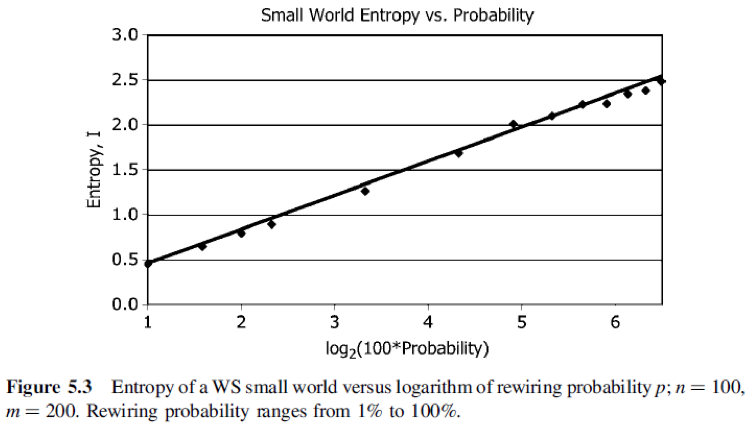
즉, 엔트로피는 확률 $p$의 log scale로 증가하게 된다. 또한 entropy의 정의에 따라 이 값은 $I_{WS} = -\sum_k h(d) \log_2 h(k) $로도 표현이 된다. 이런 결과들을 통해 우리는 small world network가 scalable하다는 것을 알 수 있는데 왜냐하면 $p$가 0이면 엔트로피의 값은 regular network와 같은 0이지만 $p$가 증가함에 따라서 우리가 원하는 entropy를 randomness를 조절함으로써 얻을 수 있기 때문이다. 따라서 이런 Small world network는 scalable하다는 것을 알 수 있다. (일단 수업에서 배운대로 정리를 하기는 했지만 이부분은 너무나도 모호하다. 아무래도 네트워크의 scalable의 definition을 추가로 찾아보고 알아봐야 할 것 같다)

Entropy vs Density

k-regular network의 density는 단순하게 $density = 2 { k \over n }$으로 계산할 수 있으며, 따라서 우리는 $k = n {density \over 2}$ 라는 사실을 알 수 있다. 이 값을 통해서 우리는 small world network의 entropy와 density의 관계를 유추할 수 있다. 즉, parameter $A, B, C$를 주고 그 값에 대해 $I_{WS(density)} = A log_2 B(density) - C $ 라는 엔트로피 식을 적을 수 있다. 이 때 $A, B, C$를 각각 0.5, 60, 0 이라고 한다면 이 식은 $I_{WS(density)} = 0.5 log_2 (60(density)) = O(log_2 (density)) = O \left(log_2 \left( \sqrt {k \over n} \right) \right)$ 임을 알 수 있다. 즉, 우리는 entropy가 density에 $O(\log_2 density)$의 형태로 표현된다는 것을 알 수 있으며 이 값은 random network의 $O(density)$보다 훨씬 덜 가파른 증가율이라는 것을 알 수 있다. 죽, 조금 더 자세히 말하자면 Small world network의 density의 증가률 혹은 rewiring probability의 증가율에 대한 entropy의 증가율은 random network의 그것보다 훨씬 더디게 증가함을 알 수 있다. 이것을 Density에 대해 ploting하게 되면 아래와 같은 결과를 얻게 된다. (일단 3개의 term 중에서 entropy만 보면 된다)

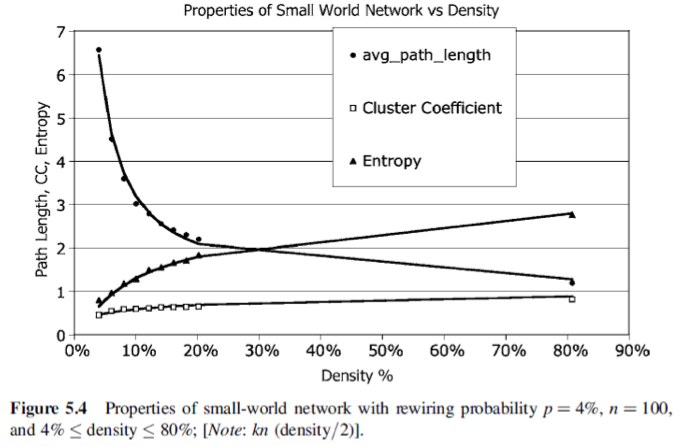
다시 한번 정리하자면, small world network에서 density와 entropy는 logarithm relationship을 가진다.

Newman, Moore, and Watts Equation

먼저 간단한 observation들을 나열해보자. 먼저 rewiring 이 없는 2-regular network는 average path가 $n \over 4k$로 표현이 된다. 그리고 바로 전 section에서 본 그림처럼 매우 작은 rewiring probability $p$에 대해서 average path length는 매우 빠르게 감소함을 알 수 있다. 그리고 마지막으로 어떤 early point $p^*$가 존재해서 이 값보다 작은 rewiring probability를 가진 small world network는 regular에 매우 가깝고 그보다 큰 값을 가지는 네트워크는 random에 더 가깝다. 이 지점을 우리는 crossover, 혹은 transition threshold라고 부르며 이런 현상을 네트워크의 phase transition이라 부른다.

Average path length는 $p=0$에서 $n \over 4k$의 값을 가지며, $p$가 증가함에 따라 감소한다. 이때 $r=2pm$이라는 값을 정의하면 $r$에 대한 path lenth scaling function을 아래와 같이 표현할 수 있다.

$$ f(r) = 4 {\tanh^{-1} {r \over \beta} \over \beta }; \ where \beta = \sqrt{r^2 + 4 r} $$

또한 average path length는 다음과 같이 표현이 된다.

$$ \bar L_{SW} = n {f(r) \over 2k} = {2n \over \beta k} tanh^{-1} {r \over \beta} $$

만약 $n=100, m=200, k=2, density=0.04, p=0.04$라는 조건을 넣고 이 값을 계산하면 average path length는 11.7이라는 값을 얻을 수 있다. 그런데 이 값은 ====

Average Path Length

작성중

$$ log_2 \bar L(r) = \log_2 \left( {n \over 4k} \right) - q \log_2 r $$

$$ \bar L(r) = {n/4k \over r^q }, \ where \ r=pkn $$

즉, 이 값들을 통해 우리는 $p$가 0이 아닐 때 (0이면 regular network와 같은 값이 된다) 이 평균 path length는 $\bar L(r) = {n/4k \over (pkn)^q }$ 로 표현된다는 것을 알 수 있다.

Clustering Coefficient

작성중

Closeness Centrality

작성중

작성중

Conclusion

자 이렇게 small world network에 대해 살펴보았다. Small world Network는 Regular Network에 확률 $p$ 만큼 randomness를 부여해 만들어지는 graph이며, 이 randomness는 scalable하며, random network와 비교했을 때 훨씬 낮은 entropy를 가진다.또한 이런 small world network의 topology는 매우 높은 clustering coefficient와 closeness를 가지게 된다. 또한 그 크기에 비해 상대적으로 짧은 average path와 diameter를 가지게 된다. (그리고 이 특성 자체가 small world effect를 지칭하는 것이기도 하다) 그리고 small world network에서 가장 좋은 search algorithm은 max-degree search 알고리듬이라는 것도 알 수 있었다.

다만, 거의 대부분의 좋은 성질을 가지고 있음에도 불구하고 Small world network 혹은 Watts-Strogatz Model에는 real network와 반하는 특성이 하나 있는데, 바로 degree distribution이다. 일반적인 real network의 degree distribution이 $P(k) \simeq k^{-\gamma}$로 표현되는 것에 비해, WS model은 exponetial degree distribution을 가지게 된다. 따라서 이런 문제를 해결하기 위해서 우리는 degree distribution이 power law distribution으로 나타나는 새로운 형태의 network인 scale-free network에 대해 다루게 될 것이다.

KAIST Network Science

다른 요약글들 보기 (카테고리로 이동)