들어가기 전에

이 글은 2014년 KAIST Network Science 수업 중 Scale Free Network 내용을 요약한 글이다. 이 렉쳐에서는 Scale Free Network라는 concept에 대해 다루게 된다.

Scale Free Network

이전 글들에서 Regular Network, Random Network와 Small world Network에 대해 다뤘던 것들 중 Path length, Clustering coefficient, 그리고 Degree distribution 부분을 정리해보자.

먼저 Path length이다. 우리가 관측하는 대부분의 network들은 Path length가 그 크기의 logarithm function으로 표현된다는 것을 알 수 있다. 조금 더 구체적으로 표현하자면 $l_{rand} \approx {\log N \over \log \bar k}$로 표현이 된다. 먼저 Regular Network의 path length는 $l \approx N^{1/D}$로 표현이 된다. 우리가 원하는 log 와는 다른 형태임을 알 수 있다. 그렇다면 Random Network와 Small world Network는 어떨까? 이전 결과들을 통해 확인할 수 있듯 $l_{rand} \approx {\log N \over \log \bar k}$로 표현이 된다는 사실을 알 수 있다. 즉, Erdös-Rényi Network와 Watts-Strogatz Network는 일반적으로 우리가 관측하는 네트워크와 비슷한 Path length를 지니고 있고 Regular Network는 그렇지 않음을 알 수 있다.

Clustering coefficient는 어떠한가? 대부분의 실제 네트워크의 clustering coefficient는 그 크기에 무관하게 항상 상수로 표현된다. 즉, $C \sim const $로 표현이 된다. Regular network와 small world network가 이 값이 상수임에 반해, Random network는 이 값이 $C = p = {\bar k \over N}$으로 표현이 된다. 즉, 크기가 커질수록 이 값이 감소하는 경향을 보이는데 이 부분은 실제 네트워크와 큰 차이가 있는 부분이다. 즉, Random network는 실제 네트워크보다 뭉침 현상이 덜 하고, Regular Network와 Small world network는 실제 네트워크와 그 뭉침 정도가 비슷하다는 것을 알 수 있다.

그렇다면 지금까지의 결론을 보면 Small world Network만 Path lenth, 그리고 Clustering의 두 가지 측면에서 실제 네트워크와 유사함을 알 수 있다. 그렇다면 마지막 Degree distribution은 어떠한가? 실제 네트워크에서 나타나는 degree distribution은 power law distribution으로 표현이 된다. 즉, $P(k) \sim k^{-\gamma}$로 표현이 된다. 그런데 Regular Network의 degree distribution은 $P(k) = \delta (k-k_d)$이며 Random Network는 $P(k) = e^{-\bar k} {\bar k ^k \over k!}$로 표현이 된다. 그리고 Small world network의 degree 역시 exponential function으로 표현이 된다. 즉, 지금까지 우리가 살펴본 그 어떤 네트워크도 실제 네트워크와 유사한 degree distribution을 보이지 않음을 알 수 있다.

이러한 문제점, 즉, degree distribution이 잘 맞지않는다는 문제점으로 인하여 새로운 Scale-Free network라는 개념이 등장하게 된다. Scale-Free network란 degree를 $k$라 했을 때 degree sequence $g’$이 power-law function $h(k) \sim k^{-q}$로 표현이 되는 네트워크를 의미한다. 이 때 exponent $q$의 값은 보통 2에서 3 사이로 결정이 된다. 수학적이지 않은 관점에서 바라본다면 scale-free network는 적은 숫자의 high degree node가 있고 그 이외의 많은 node들은 엄청 작은 degree를 가지는 네트워크를 의미한다. 그리고 이런 degree가 높은 node를 일컬어 hub라고 부르게 되며, 다시 말하자면 Scale-Free Network란 hub가 존재하는 네트워크를 의미하게 된다. 이 현상은 사실 생각해보면 우리 주변에도 많이 발생하는데, Zipf의 법칙나 Pareto의 법칙 등의 관측도 존재하고, 실제 social network에서도 친구가 엄청나게 많은 일부의 사람들이 존재하고 나머지 사람들은 그보다는 적은 사람의 친구를 가지는 등, 이미 hub라는 현상은 우리가 자연스럽게 받아들일 수 있는 개념이라는 것이다.

그렇다면 degree가 exponential인 것과 power-law인 것이 정말 크게 차이가 날까? 만약 그게 아니라면 우리는 충분히 Watts-Strogatz의 결과물을 사용할 수 있을 것이다. 아래 그 둘을 비교한 그림이 있다.

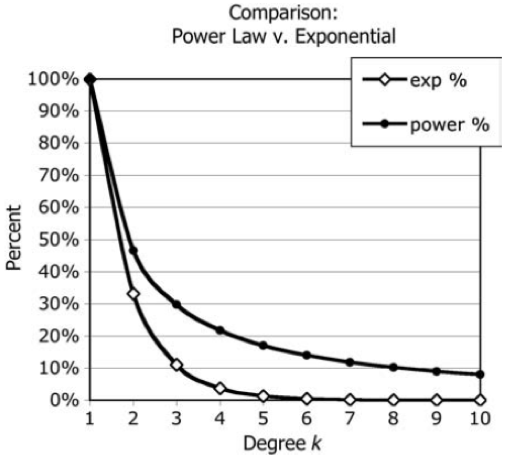
이 그림을 통해 알 수 있듯, exponential과 power-law는 그 기울기의 감소 정도가 매우 많이 차이가 난다는 것을 알 수 있고, 우리는 degree distribution이 power-law를 가지는 새로운 network가 필요하다는 것을 알 수 있다. 이런 Scale-Free Network는 1999년 Alber, Jeong, Barabasi에 의해서 처음 연구가 되었으며, 이런 네트워크를 만드는 과정을 Barabasi-Albert Procedure라고 부른다. 그렇다면 Scale-Free라는 이름은 왜 생긴 것일까? Small-world라는 말이 diameter의 증가 정도가 네트워크의 증가 속도보다 훨씬 느리기 때문에 붙은 알이라면, Scale-Free는 degree가 증가하는 정도와 실제 distribution이 같은 속도로 증가함을 의미한다. 수식으로 나타내자면 $h( \alpha k = \beta h(k)$로 표현이 된다. 즉, x-axis로 factor $\alpha$ 만큼 scaling을 한 결과는 y-axis에 factor $\beta$ 만큼 scaling을 한 것과 같다는 것이다. 따라서 이 power-law curve를 factor $\alpha$로 scaling을 하더라도 그 모양은 단순히 위아래로 움직이기만하는 형태로 표현이 된다는 것이다. 즉, 그 우리가 Scaling을 하더라도 그 형태가 변하지 않는 Scale-Free한 Network라는 것이다.

Conclusion

Scale-Free Network를 한 번 정리하고 넘어가보자. 먼저 Scale-Free란 degree distribution이 power-law로 표현되는 network이며, 토폴로지 관점에서 봤을 때 Small-world와 Random network 사이 쯤에 존재하는 네트워크이다. 아래 그림을 보면 엔트로피와 Clustering Coefficient, Average path length, hub degree를 모두 비교해본 결과인데 이 결과를 보면 다른 네트워크와 비교했을 때 다른 값들은 대체로 높지만 상대적으로 뭉침 정도가 약함을 알 수 있다.

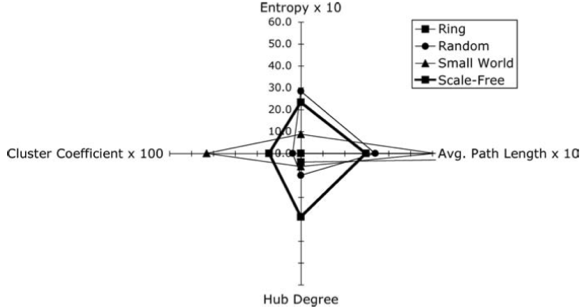
Scale-free network의 entropy는 $I(G) \sim O( \log_2 ( \Delta m) = O( \log_2 (density(n/2)))$임을 알 수 있다. 이는 small-world network의 $I(G) \sim O( \log_2 p )$와 비슷한 결과이며, 따라서 엔트로피의 관점에서 봤을 때 random network보다는 small-world network에 가까움을 알 수 있다.

Path length는 fixed n에 대해 $l = A - B k_{hub} \sim O({ \log (n) \over \log (n) + \log (density)}) $으로 표현이 된다. 그리고 cost-effectiveness라는 것도 정의가 되는데, $E = {1-\bar {l(density)} \over m}$으로 표현이 되며 Density는 $2 \frac {m} {n(n-1)}$으로 표현이 된다. ========

KAIST Network Science

다른 요약글들 보기 (카테고리로 이동)

• Lecture 1: Introduction
• Lecture 2: Graph Theory
• Lecture 3: Measures and Metric
• Lecture 4: Random Network
• Lecture 5: Small world Network
• Lecture 6: Scale free Network