README   SanghyukChun's Blog

Machine Learning 스터디 (2) Probability Theory

| Comments

들어가며

Probability thoery는 Machine Learning을 공부하기 전에 필수적으로 이해해야하는 개념들 중 하나이다. 이 글에서는 가장 기본적인 확률 개념에 대해서는 알고 있다고 가정한다. 예를 들어 independence, joint probability, marginal probability, conditional probability 등 기본적인 개념이나 $p(X) = \sum_Y p(X,Y) $ 혹은 $p(X,Y) = p(Y|X) p(X)$ 등 자주 사용되는 관계 등에 대해서는 이미 알고 있다고 생각했고, 또한 random variable 등에 대한 기본적인 지식이 이미 존재한다고 가정하고 글을 작성하였다. 만약 이런 개념들에 대해 잘 알지 못한다면 다른 글이나 강의 등을 통해 그 개념들을 먼저 이해하고 글을 읽으면 좋다.

Machine Learning - Probabilistic perspective

이전 글에서 설명했던 머신러닝의 개념을 다시 생각해보자. 머신러닝은 아래 그림처럼 설명할 수 있다.

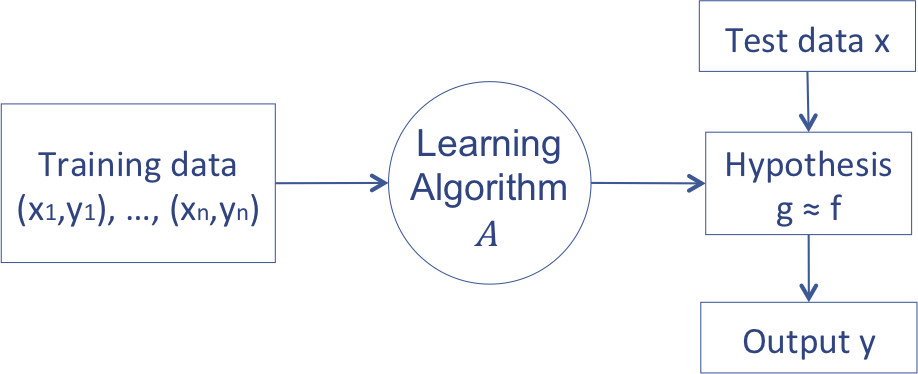
이전 글에서 나는 머신러닝이 주어진 데이터를 가장 잘 설명하는 ‘함수’를 찾는 알고리즘을 디자인하는 것이라 설명했다. 그러나 머신러닝은 확률의 관점에서도 설명이 가능하다. 머신러닝을 probability density를 찾는 과정으로 생각하는 것이다. 즉, 함수를 가정하는 것이 아니라 확률 분포를 가정하고, 적절한 확률 분포의 parameter를 유추하는 과정으로 생각하는 것이다. 주어진 데이터가 gaussian distribution으로 drawn되었다고 가정하고, 데이터와 현상을 가장 잘 설명하는 mean과 covariance를 찾는 과정과 비슷한 것이라고 생각하면 된다. 즉, 앞에서 설명한 방식은 function parameter를 찾는 방식이라면, 이제는 probability density function parameter를 찾는 것으로 바뀌는 것이다.

Maximum Likelihood Estimation (MLE)

보다 자세한 설명을 하기에 앞서, 몇 가지 개념들을 소개하고 넘어가도록 하겠다. Maximum Likelihood Estimation (MLE)는 random variable의 parameter를 estimate하는 방법 중 하나인데, 오직 주어진 Observation, 혹은 데이터들 만을 토대로 parameter estimation을 하는 방법이다. 가장 간단한 예를 들어보자. 만약 우리가 $p$의 확률로 앞면이 나오고 $1-p$의 확률로 뒷면이 나오는 동전을 던져서 $p$를 예측한다고 생각해보자. MLE로 $p$를 계산하기 위해서는 간단하게 앞면이 나온 횟수를 전체 횟수로 나누면 된다.

보다 더 자세한 설명을 위해 알려지지 않은 probability density function $f_0$가 있다고 가정해보자. 그리고 $X = (x_1, x_2, x_3, \ldots, x_n)$를 그 확률로 생성되는 Observation 이라 하자 (측정한 데이터라고 생각하면 된다). 이제 density function이 다음과 같이 $\theta$로 parameterize된 어떤 분포의 family라고 가정해보자. $\{f(\cdot|\theta)\}$. 만약 observation $x$가 주어진다면, $\theta$의 값만 알 수 있다면 바로 $f(x|\theta)$의 값을 계산할 수 있는 것이다. 만약 $f$가 가우시안이라면 $\theta$는 mean $\mu$와 covariance $\Sigma$일 것이고, Bernoulli라면 $0 \leq p \leq 1$가 될 것이다. 이렇게 정의하게 되면 Likelihood는 다음과 같이 정의할 수 있다.

$$\mathcal L (\theta;x_1, x_2, \ldots, x_n) = \mathcal L (\theta;X) = f(X|\theta) = f(x_1, x_2, \ldots, x_n|\theta) $$

Maximum Likelihood Estimation (MLE)는 $\theta$를 estimate하는 방법 중 하나로, Likelihood를 최대로 만드는 값으로 선택하는 것이다. 만약 우리가 선택하는 값을 $\hat \theta$라고 적는다면, MLE는 다음과 같은 방식으로 값을 찾는다.

$$\hat \theta = \arg\max_\theta \mathcal L (\theta;X) = \arg\max_\theta f(X|\theta)$$

참고로, 만약 observation이 i.i.d. (independent and identical distributed)하다면, $f(X|\theta) = \prod_i f(x_i|\theta)$가 되며, 여기에 log를 씌우면 덧셈 꼴이 된다. log는 단조증가함수이므로, log를 취했을 때 최대값을 가지는 지점과 원래 최대값을 가지는 지점이 동일하고, 보통 곱셈보다 덧셈이 계산이 더 간편하므로, 많은 경우에 likelihood가 아니라 log likelihood를 사용해 parameter estimation을 계산한다.

다시 원래 얘기로 돌아가보자. MLE는 가장 간단한 parameter estimation method이지만, observation에 따라 그 값이 너무 민감하게 변한다는 단점을 가지고 있다. 다시 동전 던지기를 예로 들어보자. 동전 던지기는 확률 과정이기 때문에 극단적인 경우로 $n$번을 던져서 앞면이 $n$번이 나올 수가 있다. 이 경우 MLE는 이 동전은 앞면만 나오는 동전이라고 판단해버린다. 만약 스팸필터를 만드는데 연속으로 스팸이 아닌 메일이 $n$개가 들어왔다고해서 모든 메일이 스팸이 아니라고 할 수 있을까?

Maximum a Posteriori Estimation (MAP)

MLE의 단점을 해결하기 위해 Maximum a Posteriori Estimation(MAP)이라는 방법을 사용하기도 한다. 이 방법은 $\theta$가 주어지고, 그 $\theta$에 대한 데이터들의 확률을 최대화하는 것이 아니라, 주어진 데이터에 대해 최대 확률을 가지는 $\theta$를 찾는다. 수식으로 표현하면 다음과 같다.

$$\hat \theta = \arg\max_\theta f(\theta|X)$$

MLE와 비교해 MAP는 보다 더 자연스러운 결과를 얻게 된다. MLE로 parameter estimation을 하게 되면 오직 지금 주어진 데이터만을 잘 설명하는 parameter 값을 찾게 된다. 그러나 앞서 예를 든 것처럼 만약 스팸필터를 만드는데 연속으로 스팸이 아닌 메일이 $n$개가 들어왔다고해서 모든 메일이 스팸이 아니라고 할 수 있을까? 우리가 원하는 것은 지금까지 들어온 값에 대해서만 잘 설명하는 것이 아니라 보다 더 general한 무언가를 원한다. 여러 paramter들 중에서 데이터가 주어졌을 때 가장 확률이 높은 $\theta$를 고를 수 있다면 가장 좋은 결과를 얻을 수 있을 것이다.

하지만 안타깝게도 MAP를 계산하기 위해서는 $f(\theta|X)$가 필요하지만 우리가 관측할 수 있는 것은 오직 $f(X|\theta)$뿐이다. $f(\theta|X)$를 구하기 위해서는 Bayes’ Theorem이라는 새로운 개념이 필요하다.

Bayes’ Theorem

Bayes’ Theorem은 $p(Y|X)$와 $p(X|Y)$의 관계를 표현하는 식이다. 식의 꼴은 매우 간단하지만, 이 theorem은 많은 의미를 가지고 있다. Thoerem은 다음과 같다.

$$ p(Y|X) = {p(X|Y) p(Y) \over p(X)} $$

이때 $f(X|\theta)$를 likelihood, $f(\theta)$를 prior, 그리고 $f(\theta|X)$를 posterior라고 하며 각각은 observation(likelihood), 현상에 대한 사전정보 (prior), 주어진 데이터에 대한 현상의 확률 (posterior)을 의미한다.

이 식이 중요한 이유는 우리가 관측할 수 있는 데이터 이외에도 데이터에 대한 적절한 가정이 있다면 관측한 데이터만을 사용하는 것 보다 더 우수한 parameter estimation을 가능하게 하기 때문이다.

다시 MLE와 MAP로 돌아가보자. Bayes’ Theorem을 사용하면 MAP와 MLE의 관계를 다음과 같이 적을 수 있다.

$$\hat \theta = \arg\max_\theta f(\theta|X) = \arg\max_\theta \frac{f(X|\theta) f(\theta)}{f(X)} = \arg\max_\theta \frac{\mathcal L (\theta;X) f(\theta)}{f(X)}$$

이때, $f(X)$ term은 $\theta$에 영향을 받는 term이 아니기 때문에 다음과 같이 적을 수 있다.

$$\hat \theta = \arg\max_\theta \mathcal L (\theta;X) f(\theta)$$

따라서, 만약 $f(\theta)$를 알고 있다면, MLE가 아니라 MAP를 하는 것이 가능하다. 즉, $\theta$에 대한 assumption을 사용해 결과를 더 향상시킬 수 있는 것이다. 예를 들어 우리가 시험 성적의 gaussian distribution을 estimation하고 있다고 해보자. 이 경우 mean은 반드시 시험 점수 범위 안에 포함되어야하고, 그 값을 벗어날 수 없다. 그리고 이전 시험들의 성적을 살펴보면 그 값이 대체로 40~60 점 사이에 몰려있다는 등의 정보가 있다고 가정해보자. MLE로는 이런 정보를 활용하는 것이 불가능하지만, $f(\theta)$를 가정하고, 이를 사용해 MAP를 사용할 수 있게 된다. 즉, 만약 우리가 데이터에 대한 적절한 가정을 할 수 있다면 더 나은 추론을 하는 것이 가능한 것이다. 이를 prior라고 한다. 만약 우리가 옳은 prior를 선택하게 된다면 MLE보다 MAP가 좋겠지만, 잘못된 prior를 선택하게 된다면 오히려 성능이 떨어질 수도 있다. 쉽게 생각해 prior는 일종의 ‘선입견’이다. 선입견으로 사람을 판단할 때 더 빠르게 좋은 선택을 할 수도 있지만 (이 사람은 xx씨에게 추천을 받았으니 좋은 인재겠구나) 잘못된 선입견으로 인해 나쁜 선택을 할 수도 있다 (학교가 S대가 아니니 일을 잘 못하겠지). 따라서 MAP는 데이터에 대한 정보가 아무것도 없어도 되는 MLE와는 달리, 데이터에 대한 좋은 prior를 선택하는 것이 매우 중요하다고 할 수 있다. 참고로, prior가 uniform distribution이라면 MLE와 MAP는 정확하게 같은 문제를 푸는 것과 같다.

정리하자면, Bayes’ Theorem은 더 좋은 가정이 있다면 더 좋은 유추를 할 수 있음을 보여주는 수식이다. 많은 Machine Learning Technique들이 Bayes Theorem에 근거하여 만들어졌으며, 데이터 관측과 데이터에 대한 가정을 통해 더 정확한 추론인 MAP를 가능하게 만들어주는 강력한 방법론이기도 하다.

Advanced Topic: Conjugate Prior

보통 prior는 exponential family에서 고르는 경우가 많다. Bernoulli, binomial, Poisson, Gaussian, Laplace, gamma, beta distribution 등등이 exponential family에 속한다. Exponential family를 많이 선택하는 이유는 대부분의 데이터들이 이 모양을 띄고 있기 때문이기도 하며, 만약 likelihood가 exponential family일 때, prior를 ‘좋은’ exponential family로 선택하게 되면 posterior와 prior가 같은 family에 속하게 되기 때문이다. 예를 들어 likelihood가 Bernoulli라고 하면, prior를 beta distribution으로 선택하게 되면 posterior도 beta distribution이 되며 이를 conjugate prior라고 한다.

변경 이력

  • 2014년 8월 3일: 글 등록
  • 2015년 2월 28일: 변경 이력 추가, 구성 변경 및 내용 revise

Machine Learning 스터디의 다른 글들