README   SanghyukChun's Blog

Machine Learning 스터디 (19) Deep Learning - RBM, DBN, CNN

| Comments

들어가며

이전 글에서 기본적인 neural network에 대한 introduction과, feed-forward network를 푸는 backpropagtion 알고리즘과 optimization을 하기 위해 기본적으로 사용되는 stochastic gradient descent에 대해 다루었다. 이 글에서는 deep learning이란 것은 정확히 무엇이며, 왜 deep learning이 최근 크게 급부상하게 되었는지에 대해 시간 순으로 다룰 것이다. 이 글에서는 unsupervised learning의 한 방법인 Restricted Boltzmann Machine (RBM)과 그것을 사용한 Deep Belief Network (DBN)에 대해 다룰 것이다. 또 다른 unsupervised learning 방법 중 하나인 (denoising) auto-encoder 역시 다루고자하였으나, 이 내용까지 전부 다루기에는 내용이 너무 길어져서 이 글에서는 생략하였다. 주의할 점은, 2007년 2008년에 막 deep learning이라는 이름으로 나왔던 연구들인 unsupervised pretraining 방법들은 현재 거의 쓰이지 않는 연구방법들이라는 것이다. 때문에 지금까지도 사용되는 조금 더 practical한 방법들인 neural network regularization (예를 들어서 ReLU, Dropout 등), optimization method (momentum, adagrad 등)에 대해서는 이 이후 한 번의 posting을 더 하여 다루도록 하겠다. 추가로, 오래된 work임에도 불구하고 아직도 computer vision 쪽에서 엄청나게 많이 사용하는 Convolutional Neural Network (CNN) 에 대해서도 다루도록 하겠다.

Deep Neural Network

Deep learning이라는 것은 사실 deep neural network를 의미하는 것이다. Neural network에 대해서는 이전 글에서 설명하였고, 그럼 deep이란 무엇인가하면, 다른게 아니라 feed-forward network에서 가운데 hidden layer가 1개 보다 많으면 ‘deep’하다고 말하는 것이다. 요즘은 layer를 무조건 1개보다는 많이 쌓기 때문에 요즘 나오는 neural network 연구는 모두 deep learning 연구라고 생각하면 된다.

그런데 사실 deep learning은 전혀 새로운 연구분야가 아니고 이미 몇 십년 전에 기본적인 연구가 끝난 분야이다.

  • 1958 Rosenblatt proposed perceptrons
  • 1980 Neocognitron (Fukushima, 1980)
  • 1982 Hopfield network, SOM (Kohonen, 1982), Neural PCA (Oja, 1982)
  • 1985 Boltzmann machines (Ackley et al., 1985)
  • 1986 Multilayer perceptrons and backpropagation (Rumelhart et al., 1986) 1988 RBF networks (Broomhead&Lowe, 1988)
  • 1989 Autoencoders (Baldi&Hornik, 1989), Convolutional network (LeCun, 1989) 1992 Sigmoid belief network (Neal, 1992)
  • 1993 Sparse coding (Field, 1993)

이렇듯 이미 가장 중요한 기초적인 연구는 예전에 다 끝났다. 지난 글에서 설명한 backpropagation 알고리즘은 이미 1986년 나온 알고리즘이고, 1989년에 나온 convolutional network가 요즘도 vision 분야에서 늘 사용하는 그 CNN이다. 그런데 정작 deep learning은 2000년도 중반이 지나고나서야 주목을 받기 시작했다. 왜 그랬을까?

Why Deep Learning?

Deep learning이 예전에 ‘사기꾼’ 취급을 받았던 이유는 크게 세 가지 이유가 있었다. 먼저 ‘deep’ learning에 대한 이론적인 결과가 전무했다는 점 (network가 deep 해지면 문제가 더 이상 convex해지지 않는데, 이 상태에 대해 좋은 convergence는 어디이며 어떤게 좋은 initialization인가 등에 대한 연구가 전무하다. 즉, learning하면 overfitting이 너무 심하게 일어난다), 둘째로 이론적으로 연구가 많이 진행되어있는 ‘deep’ 하지 않은 network (perceptron이라고 한다) 는 xor도 learning할 수 없는 한계가 존재한다는 점 (linear classifier라 그렇다). 마지막으로 computation cost가 무시무시해서 그 당시 컴퓨터로는 도저히 처리할 엄두조차 낼 수 없었다는 점이다.

그렇다면 지금은 무엇이 바뀌었길래 deep learning이 핫해진걸까? 가장 크게 차이 나는 점은 예전과는 다르게 overfitting을 handle할 수 있는 좋은 연구가 많이 나오게 되었다. 처음 2007, 2008년에 등장했던 unsupervised pre-training method들 (이 글에서 다룰 내용들), 2010년도쯤 들어서서 나오기 시작한 수많은 regularization method들 (dropout, ReLU 등). 그리고 과거보다 하드웨어 스펙이 압도적으로 뛰어난데다가, GPU parallelization에 대한 이해도가 높아지게 되면서 에전과는 비교도 할 수 없을정도로 많은 computation power를 사용할 수 있게 된 것이다. 현재까지 알려진바로는 network가 deep할 수록 그 최종적인 성능이 좋아지며, optimization을 많이 하면 할 수록 그 성능이 좋아지기 때문에, computation power를 더 많이 사용할 수 있다면 그만큼 더 좋은 learning을 할 수 있다는 것을 의미하기 때문에 하드웨어의 발전 역시 중요한 요소이다.

그리고 무엇보다 무시할 수 없는 것은, deep learning 기반의 approach들이 다른 방법론들을 압도하는 분야들이 있다는 것이다. 대표적인 분야가 바로 computer vison이다. 우리가 잘 알고 있는 MNSIT 데이터셋은 물론이고, ImageNet과 그것 중에서 10개의 class만 떼어내서 만들어낸 데이터셋인 Cifar-10 대해서도 가장 잘 하고 있는건 역시 neural network이다. 아래 표들을 살펴보자 (출처)

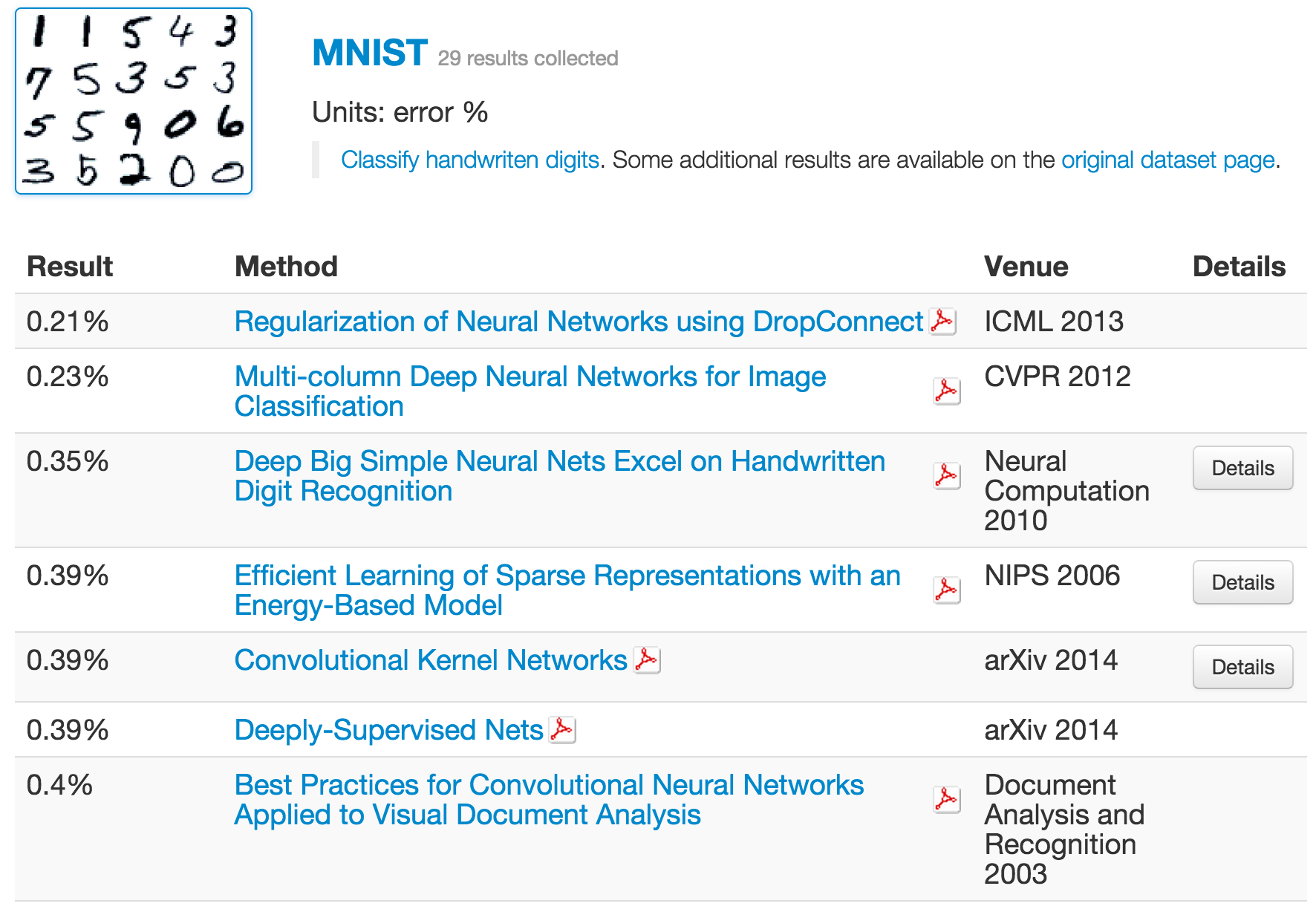
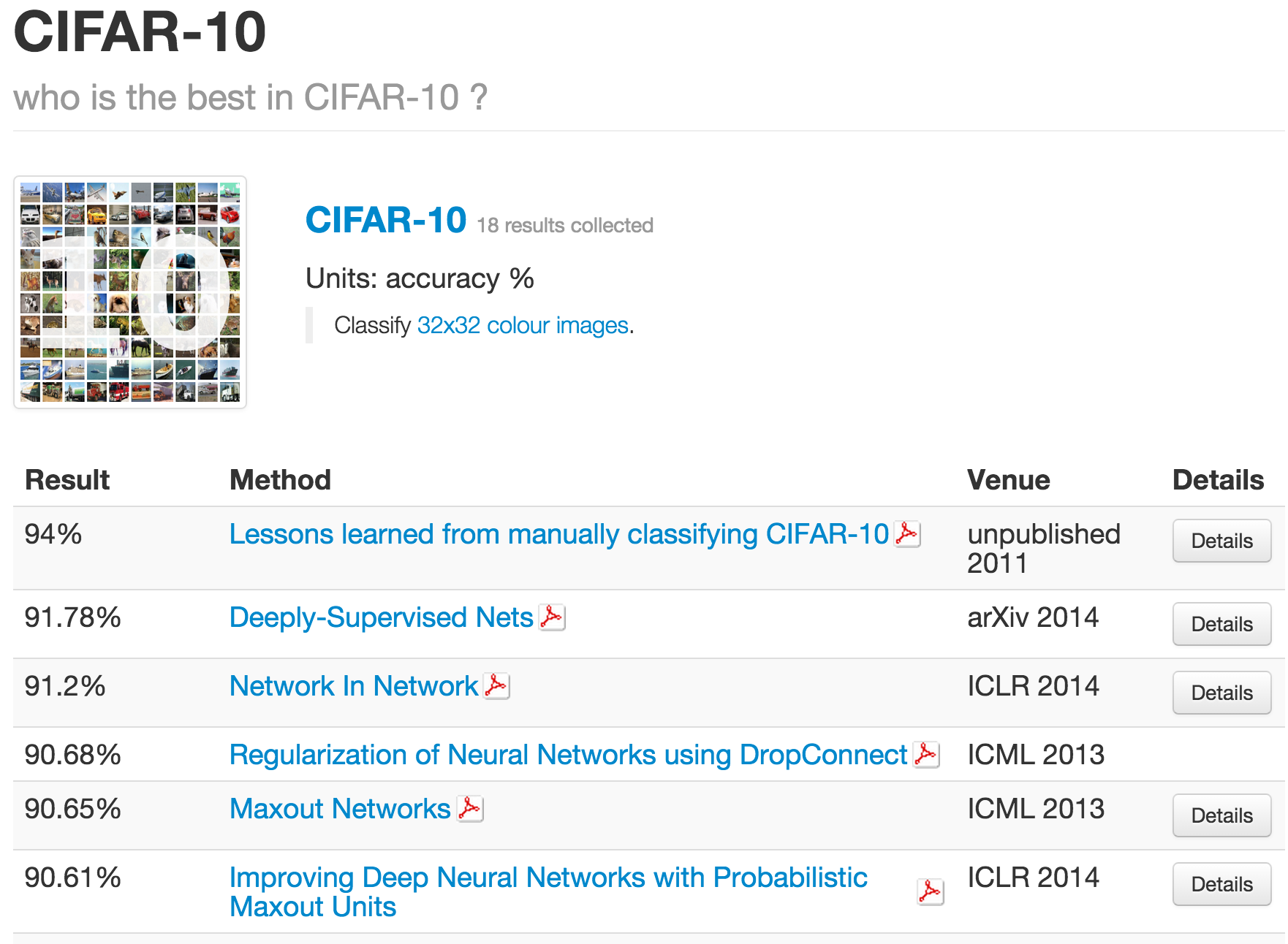
여기서 잠시 MNIST가 28 by 28 짜리 handwrite digit을 모아놓은 데이터셋이라는 것은 많이 언급했던 내용이니 넘어가고, ImageNet competition에 대해 잠깐 언급하고 넘어가보도록 하자. ImageNet이라는 것은 사실 데이터셋의 이름이 아니라 매년 새로운 task가 주어지는 competition이다. 보통 실험에 사용하는건 2012년 데이터셋 (ILSVRC 2012)인데, training 데이터가 1000개 class에 데이터 개수는 거의 128만개 가까이 되는 엄청나게 큰 데이터 셋이다. Test data는 공개되지 않았고, 대신 validation set으로 공개된 데이터는 총 5만개짜리 데이터이다. 전체 데이터 사이즈는 거의 150GB가까이 된다. 이때 데이터를 많이 사용하는 이유는, 이때 task가 iamge classification이고, 많은 논문들이 이 때의 데이터를 기준으로 실험하기 때문인듯 하다. 예를 들어서 ILSVRC 2015에는 더 이상 classification task가 존재하지 않고, object detection이나 object localization등의 task만 주어져있는 상태이다.

현재 ImageNet dataset (혹은 ILSVRC 2012)에서 state-of-art classification performance를 보이는 work은 지난 번에 review했던 Batch Normalization 논문인데, classification error는 20.1%이고, 1000개의 class 중에서 확률이 가장 높다고 판단한 top 5개 중에서 우리가 원하는 정답이 있을 확률인 top-5 error는 4.9%에 달한다. ImageNet dataset을 보면 1000개의 데이터가 전부 독립적인 것이 아니라 어느 정도 비슷한 데이터도 섞여있는 만큼, top-5 error가 5% 이하라는 것은 진짜 어마어마한 수준이라고 할 수 있다.

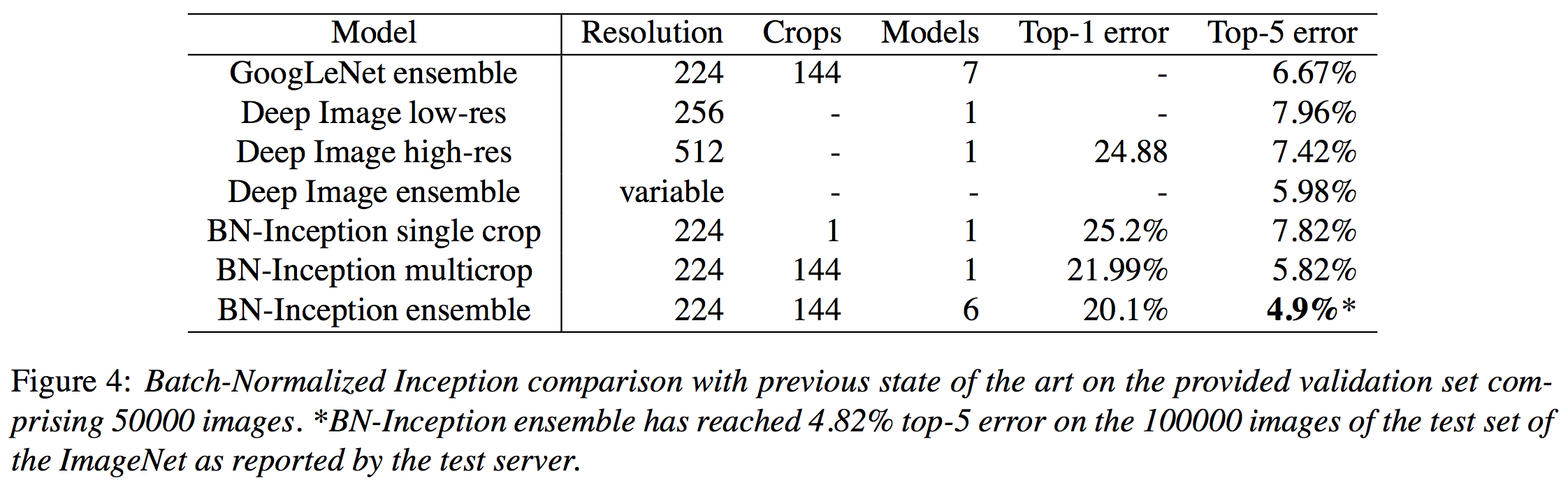
이렇듯 deep learning은 computer vision 쪽에서 압도적인 성능을 보이고 있을 뿐 아니라, 최근에는 language model, NLP, machine translation 등의 다양한 분야에서도 좋은 결과를 내고 있다. 무엇보다 deep learning 쪽 분야는 Google, MS, Yahoo 심지어는 Apple과 삼성 등에서도 투자를 많이 하고 있고 실제로 엄청나게 많은 연구들이 행해지고 그 연구들이 나오자마자 거의 바로 산업에 적용될 정도로 practical하게 많이 쓰이고 있는 분야가 되었다. 그렇기 때문에 아마도 당분간은 머신러닝 분야에서 deep learning의 강세는 이어질 것으로 보인다.

이 글의 남은 부분의 첫 번째 부분에서는 NIPS 2006에 발표된 Bengio 교수 연구팀의 Greedy layer-wise training of deep networks 연구와 NIPS 2007에 발표된 Hinton 교수 연구팀의 A fast learning algorithm for deep belief nets 두 논문을 통해 제안되었던 unsupervised pretraining method 들에 대해서 다룰 것이다. 이 부분은 더 이상 practical usage로 사용되지는 않지만, deep learning의 거의 첫 번째 연구결과라고 해도 좋을 정도로 의미있는 연구결과들이므로 한 번쯤 알아둘 필요가 있다고 생각한다.

그리고 나머지 부분에서는 정말 오래된 연구결과이지만 아직까지도 쓰이고 있는 Convolutional Neural Network (CNN)에 대해 다룰 것이다. 이 결과는 앞서 ImageNet에서 가장 좋은 결과를 내고 있다는 Batch Normalization 에서도 기본 골격으로 사용하고 있는 vision 쪽에서는 가장 기초가 되는 엄청나게 중요한 개념이므로 마찬가지로 이 글에서 다루도록 하겠다. 만약 practical한 목적으로 이 글을 읽고 있다면 아래 unsupervised pretraining 섹션은 건너뛰고 바로 CNN 섹션부터 읽더라도 크게 상관없다.

Problems to solve for deep learning

Deep learning이 흥하기까지 수 많은 연구결과들이 있었지만, 지금처럼 deep learning이 hot하게 되기까지는 앞에서 말했던 것처럼 regularization method들이나 initialization method들, 그리고 overfitting을 최대한 피할 수 있는 optimization mehtod 등이 많이 제안되면서부터라고 할 수 있다. 이 연구들이 공통적으로 고민하고 있는 것은 overfitting이다.

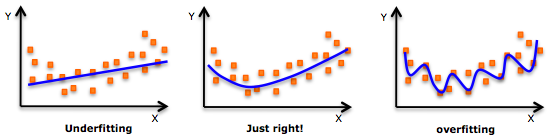
Overfitting은 주어진 데이터의 양에 비해 모델의 complexity가 높으면 발생하게 된다. 안타깝게도 neural network가 깊어질수록 model의 complexity는 exponential하게 증가하게 된다. 그렇기 때문에 거의 무한한 표현형을 learning할 수 있는 deep network가 좋다는 것을 다들 알고 있음에도 불구하고, 너무나 overfitting이 심하게 발생하기 때문에 neural network 연구가 멈추게 된 것이다. 하지만 2007~8년 즈음하여 overfitting을 막기 위하여 새로운 initialziation을 제안하는 work이 나오게 되는데 그 work이 바로 앞에서 설명 했던 NIPS에 발표되었던 두 work이다.

먼저 Restricted Boltzmann Machine (RBM) 에 대해 설명해보자.

Restricted Boltzmann Machine (RBM): Introduction

이 섹션은 상당히 수식이 많으며, 너무 복잡한 수식은 생략한 채 넘어가기 때문에 다소 설명이 모자랄 수 있다. 조금 더 관심이 있는 사람들을 위하여 아래의 참고자료들을 추천한다. 난이도 순서대로 당장 필요한 정도에 따라 읽으면 좋을 것 같은 순서대로 배치하였다. 내가 생각했을 때 알고리즘에 대한 심층적인 이론적 설명이 많은 순서대로 나열하였으니 처음부터 천천히 읽어보면 좋을 것 같다. 특히 마지막 참고자료는 상당히 이론적인 내용들을 굉장히 차근차근 어렵지 않게 담고 있으므로, RBM을 제대로 공부하고 싶다면 꼭 읽어보면 좋을 것 같다.

RBM은 graphical probabilistic model의 일종으로, undirected graph로 표현되는 모델이다. Probability는 energy function의 형태로 표현이 되는데, 원래 RBM이라는 모델 자체가 Ising model이라는 물리 분야에서 많이 사용되는 모델의 일종이기 때문에 그 형식을 그대로 본 따온 것으로 보인다. RBM의 기본적인 형태는 다음과 같다.

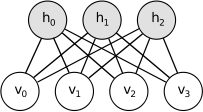
이 모델은 complete undirected bipartite graph을 띄고 있다. 이때 각각의 biparition은 visual unit들과 hidden unit들로 이루어져있으며 이 경우는 모든 unit들이 binary인 경우에 대해서만 다룬다. 따라서 visual layer와 hidden layer는 서로 internal edge가 존재하지 않고, layer들끼리 undirected fully connected된 형태를 띄고 있다. 이 모델은 graphical probabilistic model이기 때문에 각각의 visual node $v$들과 hidden node $h$들은 random variable을 의미하게 되며, 이 모델은 $v,h$의 joint probability를 표현하는 모델이 된다. 이 모델은 joint probability를 아래와 같은 energy function form으로 표현한다.

$$p(v,h) = \frac{e^{-E(v,h)}}{Z}, \mbox{ where } E(v,h) := -\sum_i a_i v_i - \sum_j b_j h_j - \sum_i \sum_j v_i w_{ij} h_j \mbox{ and } Z = \sum_{v,h} e^{-E(x,h)} $$

RBM의 parameter는 bais term $a_i, b_j$와 weight term $w_{ij}$로, 이 값들이 변화함에 따라 joint probability가 변하게 된다. RBM은 주어진 데이터들을 가장 잘 설명하는, 즉 $p(v)$의 값이 가장 커지도록 하는 parameter를 learning하게된다. 보통 이 값은 log likelihood로 다음과 같이 표현된다.

$$\theta = \arg\max_\theta \log \mathcal L (v) = \arg\max_\theta \sum_{v \in V} \log P(v). $$

이때 likelihood $P(v)$는 $P(v) = \sum_h P(v,h) = \frac{1}{Z} \sum_h e^{-E(v,h)}$로 계산할 수 있다. 이 log-likelihood 값을 maximize하는 문제는 non-convex문제이기 때문에 global optimum을 찾는 것은 불가능하고, 대신 stochastic gradient descent를 사용하여 local optimum을 계산하게 된다. SGD를 사용해 update를 하기로 하였으니, 각각의 sample $v$에 대한 gradient $\frac{\partial\log p(v)}{\partial\theta}$를 계산해보자.

$$ \log p(v) = -\log \frac{1}{Z}\sum_h e^{-E(v,h)} = \ln \sum_h e^{-E(v,h)} - \ln \sum_{v,h} e^{-E(v,h)}$$

$$ \frac{\partial\log p(v)}{\partial\theta} = \frac{\partial\ln \sum_h e^{-E(v,h)}}{\partial\theta} - \frac{\partial\ln \sum_{v,h} e^{-E(v,h)}}{\partial\theta}$$

$$ = -\frac{1}{\sum_h e^{-E(v,h)} } \sum_h e^{-E(v,h)} \frac{\partial E(v,h)}{\partial \theta} + \frac{1}{\sum_{v,h} e^{-E(v,h)} } \sum_{v,h} e^{-E(v,h)} \frac{\partial E(v,h)}{\partial \theta}$$

$$ = -\sum_h p(h|v) \frac{\partial E(v,h)}{\partial \theta} + \sum_{v,h} p(v,h) \frac{\partial E(v,h)}{\partial \theta}.$$

이때, $p(h|v)$는 $p(h|v) = \frac{p(v,h)}{p(v)} = \frac{ e^{-E(v,h)} }{\sum_h e^{-E(v,h)}}$ 로부터 유도되는 값이다. 즉, 우리가 optimization하고 싶은 gradient는 $\frac{\partial E(v,h)}{\partial \theta}$의 값의 $p(h|v)$와 $p(v,h)$에 대한 expectation 값이 된다. 예를 들어 $w_{ij}$의 경우 $\frac{\partial E(v,h)}{\partial w_{ij}} = v_i h_j$이므로 $v_i h_j$의 $p(h|v)$와 $p(v,h)$에 대한 expectation을 구하게 된다면 우리가 목표하는 gradient를 얻는 것이 가능하다.

$$ \frac{\partial\log p(v)}{\partial\theta} = \sum_h p(h|v) v_i h_j - \sum_{v,h} p(v,h) v_i h_j$$

$$ = \sum_h p(h|v) v_i h_j - \sum_{v,h} p(v,h) v_i h_j = p(h_j=1|v) v_j - \sum_v p(v) p(h_j=1|v)v_j$$

라는 결과를 얻을 수 있다. (지금은 i와 j가 고정된 상황이므로 $\sum_h$를 하게 되면 $h_j$의 값이 0이거나 1인 경우 둘 밖에 없고, 0인 경우는 $v_i h_j$가 0이므로 위와 같은 식을 얻을 수 있다). 이때, $p(h_j = 1|v)$는 아래와 같이 간단하게 계산할 수 있다.

$$p(h_j = c|v) = \frac{1}{Z} exp(-\sum_i a_i v_i - \sum_{\ell\neq j} b_\ell h_\ell - b_j * c - \sum_i \sum_{\ell\neq j} v_i w_{i\ell} h_\ell - \sum_i v_i w_{ij} * c)$$

$$p(h_j = 1|v) = \frac{p(h_j = 1|v)}{p(h_j = 1|v) + p(h_j = 0|v)} = \frac{1}{1 + exp(-b_j-\sum_i v_i w_{ij})} = \sigma(b_j+\sum_i v_i w_{ij}).$$

즉, conditional probability는 sigmoid function이 된다. 마찬가지로 $p(v_i = 1 | h) = \sigma(a_i+\sum_j h_j w_{ij})$로 계산할 수 있다. 그렇기 때문에 우리가 주어진 데이터 $v_i$도 알고 있고, $p(h_j=1|v)$ 역시 sigmoid로 계산할 수 있기 때문에, log likelihood의 weight에 대한 gradient값인 $\sum_h p(h|v) v_i h_j - \sum_{v,h} p(v,h) v_i h_j$의 앞부분은 간단하게 계산할 수 있다.

그러나 문제가 되는 부분은 뒷 부분이다. 안타깝게도 이 경우는 모든 $v,h$의 조합에 대해 값을 모두 계산해야하기 때문에 이 값을 정확하게 계산하기 위해 필요한 computational complexity는 exponential이 된다. 그런데 이 값이 정확하게 우리가 구하고 싶은 마지막 final 값도 아니고, 겨우 중간 단계의 한 번의 gradient를 계산하기 위해 필요한 step에 불과한데 iteration 안에 exponential complexity를 가지는 step이 있는건 큰 문제가 된다. 그렇기 때문에 이 RBM문제를 해결하기 위해 도입되는 알고리즘이 Contrastive Divergence라는 gradient approximation 알고리즘이다.

Restricted Boltzmann Machine (RBM): Contrastive Divergence

Contrastive Divergence 알고리즘을 한 마디로 요약하면: $p(v,h)$를 계산하는 MCMC (Gibbs Sampling)의 step을 converge할 때 까지 돌리는 것이 아니라, 한 번만 돌려서 $p(v,h)$를 approximate하고, 그 값을 사용하여 $\sum_{v,h} p(v,h) v_i h_j$을 계산해 gradient의 approximation 값을 구한다.

MCMC는 원하는 stationary distribution을 가지는 MC를 design하여 목표로하는 distribution을 만들어내는 알고리즘 family를 일컫는다. 이 내용도 꽤나 방대한 내용이므로, 필요하다면 나중에 추가로 포스팅을 하도록 하겠다. Gibbs Sampling은 MCMC 알고리즘 family 중 하나로, 여러 random variable들의 joint probability를 계산하기 위한 알고리즘이다. 사실 내용은 엄청 간단한데, 한 variable을 제외한 나머지 r.v.를 fix하고 나머지 fixed된 r.v.가 주어졌다고 가정하고 conditional probability를 구해 현재 r.v.를 update하는 것을 모든 variable들에 대해 distribution이 converge할 때까지 반복하는 것이다. 이 과정을 엄청나게 많이 반복해서 stationary distribution에 converge했을 정도로 많이 iteration을 돌리게 되면, 우리는 iteration을 돌리면서 얻어내는 sequence들로부터 r.v.들의 joint probability로부터 sample하는 것과 같은 확률로 sample들을 얻을 수 있다.

따라서 이 알고리즘을 사용하면 앞에서 exponential complexity가 문제가 되었던 $p(v,h)$를 계산하는 것이 가능하다. 그런데 문제는 보통 MCMC가 converge할 때 까지 걸리는 시간이 결코 적지 않다는 것이다. 이론적으로 polynomial complexity를 보장할 수는 있지만, 실제 leanring time이 너무 길어져서 practical하게 쓰기 어렵다. 앞에서 설명한 것 처럼 이 distribution이 한 번의 gradient update만을 위해 사용되는 RBM에서는 그 시간을 모두 사용하기에는 너무 비효율적이다.

그래서 RBM은 Gibbs sampleing을 끝까지 돌리는 대신 이런 생각을 하게 된다. ‘어차피 정확하게 converge한 distribution이나, 중간에 멈춘 distribution이나 대략의 방향성은 공유할 것이다. 그렇기 때문에 완벽한 gradient 대신 Gibbs sampling을 중간에 멈추고 그 approximation 값을 update에 사용하자.’ 이 아이디어가 바로 Contrastive Divergence의 전부라고 할 수 있다. Contrastive Divergence는 전체 RBM update 과정 중에서 이 Gibbs sampling을 한 번만 돌리는 부분을 일컫는 말이며, Hinton이 처음 제안한 이후 나중에 이 알고리즘이 충분한 시간이 흐른 후에 전체 log likelihood의 local optimum으로 converge한다는 이론적 결과까지 증명된다.

Contrastive Divergence를 도입한 RBM update 알고리즘은 다음과 같다. (notation이 조금 다를 수 있다)

이 과정을 계속 반복하면 우리가 원래 원했던 hidden node와 visible node들의 joint probability를 표현하는 RBM을 learning할 수 있게 된다. RBM이 이렇게 간단하게 learning되는 이유는 restricted라는 조건이 있기 때문이다. 즉, 같은 layer들끼리는 connection이 없기 때문에 $p(h|v) = \prod_j p(h_j|v)$로 간단하게 표현되기 때문에 leanring이 간단해지는 것이다. 그렇기 때문에 restricted 되지 않은 general boltzmann machine은 RBM 처럼 마냥 간단하게 update되지 않는다.

Deep Beilf Network (DBN)

DBN은 $\ell$ 개의 layer를 가진 joint distribution을 표현하는 graphical model이다. 참고로 앞에서 RBM은 1-layer 모델이었다. DBN의 확률 모델은 다음과 같은 식으로 표현된다. 이때 $h^k$는 k번째 layer의 hidden variable들을 표현하는 notation이다.

$$P(x, h^1, \ldots, h^\ell) = \bigg( \prod_{k=1}^{\ell-2} P(h^k|h^{k-1}) \bigg) P(h^{\ell-1},h^{\ell})$$

이때 data $x$는 $h^0$이고, 각각의 $P(h^k|h^{k-1})$는 RBM에서 visible unit이 given된 conditional probability로 표현되고, joint probability $P(h^{\ell-1},h^{\ell})$는 RBM의 joint probability로 given된다. 이 모델은 아래와 같은 알고리즘으로 learning할 수 있다.

즉, 이 모델은 RBM을 맨 아래 data layer부터 차근차근 stack으로 쌓아가면서 전체 parameter를 update하는 모델이다. 이 모델을 그림으로 표현하면 아래와 같은 그림이 된다.

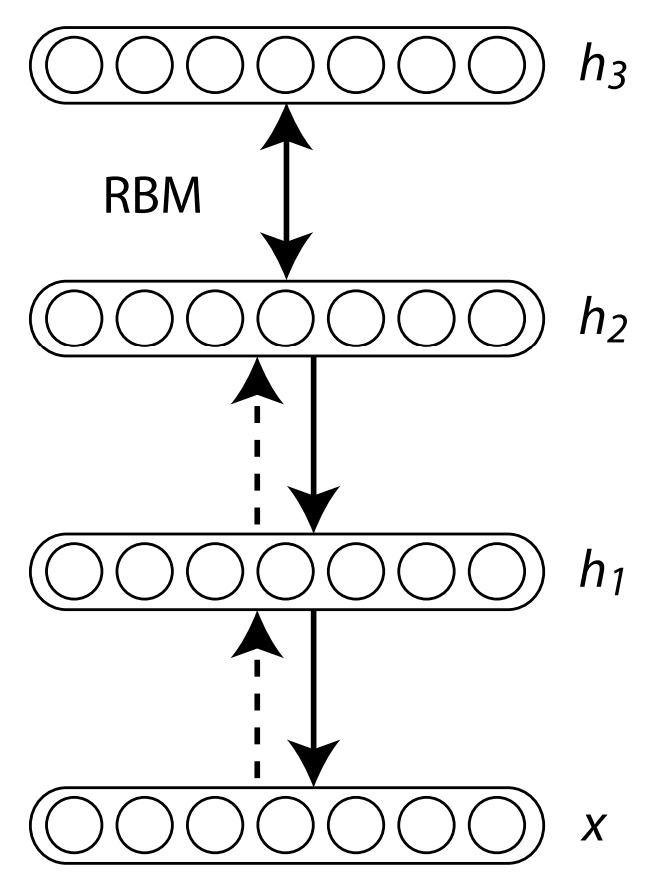
마지막 layer는 joint probability를 의미하고, 나머지 layer들은 모두 conditional probability로 표현된다. 참고로 전체를 jointly하게 표현하는 모델을 Deep Boltzmann Machine (DBM) 이라고 하는데, 이 모델의 경우 RBM update를 하는 알고리즘과 비슷한 알고리즘으로 전체 모델을 update하게 된다. 그러나 이 논문이 발표될 당시에는 DBN이 훨씬 간단하고 computational cost가 적기 때문에 DBN이라는 모델을 제안한 것으로 보인다.

이 모델이 의미있는 이유는 joint probability를 잘 표현하는 좋은 graphical model이어서가 아니라, 이 모델로 deep network를 pre-training하고 backpropagation 알고리즘을 돌렸더니 overfitting 문제가 크게 일어나지 않고 MNIST 등에서 좋은 성과를 거뒀기 때문이다. 즉, parameter initialization을 DBN의 joint probability를 maximize하는 (layer-wise로 $\ell$개의 RBM을 learning하는) 방식으로 하고 나서, 그렇게 구해진 parameter들로 deep network를 initialization하고 fine-tuning (backpropation) 을 했을 때, 항상 그 정도 size의 deep network에서 발생하던 overfitting issue가 사라지고 성능이 우수한 classifier를 얻을 수 있었기 때문이다.

DBN으로 unsupervised pre-training한 deep network 모델을 사용했을 때 MNIST 데이터 셋에서 그 동안 다른 모델들로 거뒀던 성능들보다 훨씬 우수한 결과를 얻을 수 있었고, 그때부터 deep learning이라는 것이 큰 주목을 받기 시작했다. 그러나 지금은 데이터가 충분히 많을 경우 이런 방식으로 weight를 initialization하는 것 보다 random initialization의 성능이 훨씬 우수하다는 것이 알려져있기 때문에 practical한 목적으로는 거의 사용하지 않는다.

Convolutional Neural Network (CNN): Introduction

DBN이 지금은 practical한 목적으로 거의 사용되지 않는 것과는 대조적으로, 1989년에 제안된 이 모델은 아직까지도 많이 쓰이는 deep network 모델이다. 특히 computer vision에 특화된 이 네트워크는 인간의 시신경 구조를 모방하여 인간이 vision 정보를 처리하는 것을 흉내낸 모형이다.

DBN은 overfitting issue를 initialization으로 해결하였지만, CNN은 overfitting issue를 모델 complexity를 줄이는 것으로 해결한다. CNN은 convolution layer와 pooling layer라는 두 개의 핵심 구조를 가지고 있는데, 이 구조들이 model parameter 개수를 효율적으로 줄여주어 결론적으로 전체 model complexity가 감소하는 효과를 얻게 된다.

Convolutional Neural Network (CNN): Convolution Layer

먼저 convolution layer에 대해 설명해보자. Convolution layer를 설명하기 전에 먼저 convolution operation에 대해 알아보자. Convolution이란 signal processing 분야에서 아주 많이 사용하는 operation으로, 다음과 같이 표현된다.

$$s(t) = (x * w)(t) = \int x(a)w(t-a) da.$$

예를 들어 이 operation은 주어진 데이터 $x$에 filter $w$를 사용해 데이터를 처리할 때 사용된다. 이 operation을 적용한 간단한 예를 보자. (출처)

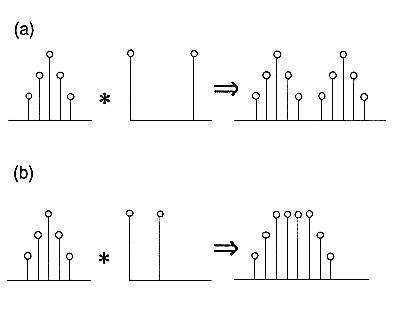
이렇듯 convolution은 어떤 filter를 사용하여 주어진 image의 적절한 feature를 뽑아내기 위해 사용했던 operation이다. 이때 $s(t)$를 데이터 $x$의 feature map이라고 부른다. Deep learning이 널리 사용되기 이전에는 다른 머신러닝 framework에 이미지를 input으로 넣고 처리하기 위해서는 먼저 filter를 고르고 그 filter로 image를 convolution하는 preprocessing을 거쳐서 적절한 feature map을 얻어낸 이후에 그것을 machine learning framework의 input으로 넣어 돌리는 방식을 사용했었다. 그렇기 때문에 이런 feature engineering이 전체 performance에 큰 영향을 미치는 경우가 많았다. 어떤 filter를 선택할 것이며, 얼마나 많은 filter를 고를 것인지 등의 영역은 feature engineering의 영역이고, 이론적인 영역이 아니기 때문에 machine learning 분야에서는 큰 관심을 두는 분야는 아니었다. 데이터는 잘 처리되었다고 가정하고 그 데이터를 사용해 어떤 좋은 알고리즘을 개발하느냐가 그 동안 머신러닝 framework들의 아이디어였다면, CNN의 핵심 아이디어는 preprocessing이 실제 performance에 크게 영향을 미치니까, 아예 이 preprocessing을 가장 잘해주는, 가장 좋은 feature map을 뽑아주는 convolution filter를 learning하는 모델을 만들어버리자는 것이다.

최대한 작은 complexity를 가지면서 우수한 filter를 표현하기 위한 CNN의 핵심 아이디어는 다음 세 가지이다: sparse interactions (혹은 sparse weight라고도 한다), parameter sharing (혹은 tied wieght라고도 한다), equivariant representations. 즉, CNN은 layer와 layer간에 모든 connection을 연결하는 대신 일부만 연결하고 (sparse weight), 그리고 그 weight들을 각각 다른 random variable로 취급하여 따로 update하는 대신 특정 weight group들은 weight 값이 항상 같도록 parameter를 share한다 (parameter sharing). 그리고 앞의 아이디어를 잘 활용하여 shift 등의 transform에 대해서 equivariant한 (자세한 내용은 밑에서 설명한다) representation을 learning하도록 모델을 구성한다.

Sparse weight를 사용하게 되면 모든 가능한 connection을 사용하는 것 보다 훨씬 적은 표현형을 learning하게 된다는 단점이 있지만, 반대로 model의 complexity가 낮아진다는 장점이 존재한다. CNN은 vision과 관련된 task를 수행하도록 design된 network라는 것은 이미 언급한바 있다. 이런 vision 데이터를 처리하는 task를 하게 될 경우에는 주어진 input의 dimension에 비해 실제 필요한 feature의 dimension은 극히 적다는 domain knowledge를 우리는 이미 가지고 있다. 즉 input인 이미지의 경우 픽셀 값이 적으면 몇 백에서 많으면 몇 백만에 이를 정도로 dimension이 엄청나게 높지만, 우리가 필요한 ‘feature’는 그 중에서도 극히 일부 영역, 이를테면 edge detection 등의 그에 비해 훨씬 적은 dimension으로 표현 가능하기 때문에 최대한 parameter를 줄여서 더 효율적인 feature map을 뽑아내기 위하여 weight를 sparse하게 사용한다. 이를 그림으로 표현하면 아래와 같다.

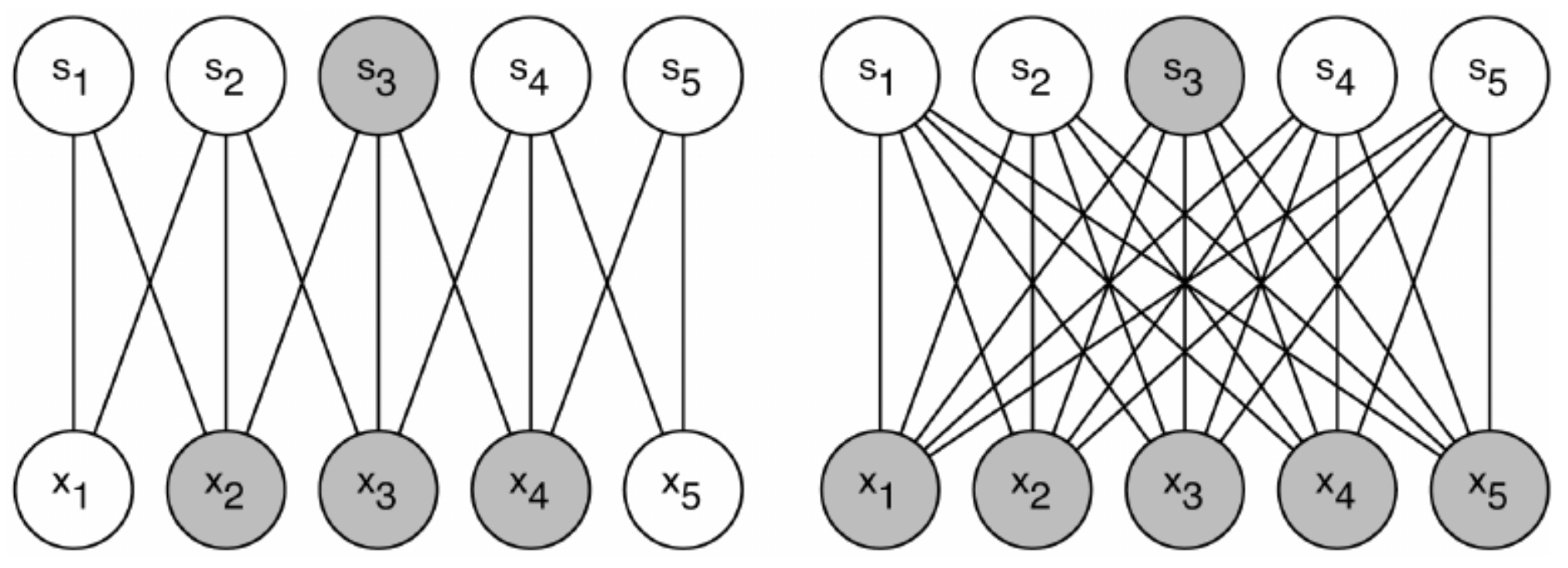
이 그림은 같은 output $s_3$에 영향을 주는 edge들과 input node를 표현한 그림이다. 왼쪽은 가능한 connection이 전부 있는 것이 아니라 그 일부만 존재하고, $s_3$에 영향을 주는 input이 $x_2, x_3, x_4$ 뿐이지만 오른쪽은 모든 가능한 connection이 있어서 model parameter의 개수가 크게 차이나고 모든 input이 $s_3$에 영향을 주는 것을 알 수 있다. 실제 image 데이터를 처리하기에는 왼쪽 모델이 조금 더 나은데, 그 이유는 한 feature를 결정하기 위해서 모든 image 정보가 필요한 것이 아니라, image의 일부분만 필요하기 때문이다. 예를 들어 내가 face segmentation, 즉 얼굴 사진에서 눈 코 입 등을 찾아내는 task를 수행한다고 하면, 주어진 사진에서 ‘눈’이 어디인지 표현하기 위해서 모든 이미지가 다 필요한 것이 아니라 눈 주변의 local한 데이터만 필요할 것이라고 유추할 수 있다. 오른쪽 그림은 필요하지 않은 배경까지 모두 고려하여 눈에 대한 정보를 찾는 셈이고, 왼쪽 그림은 local한 정보만을 주고 눈에 대한 정보를 처리하게 하는 것이다. 따라서 vision task를 처리하기에는 적절한 sparse weight가 더 효율적인 모델이라는 것을 알 수 있다. 때문에 CNN의 convolution layer는 hidden node 하나가 image의 local한 patch와 연결되어있는 형태로 되어있다. 예를 들어 한 hidden node 마다 image의 3 by 3 patch만을 연결하는 방식이다. 그림으로 표현하면 아래와 같은 식이다. (출처: Code project - Online handwriting recognition using multi convolution neural networks)

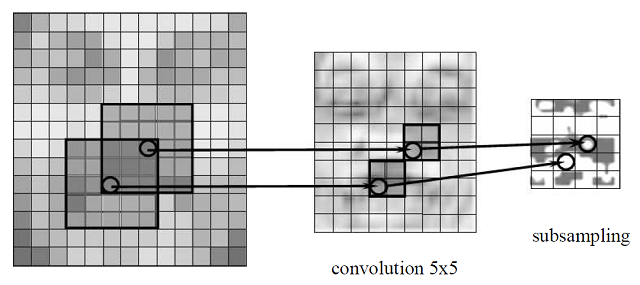
여기에서 subsampling은 일단 나중에 설명하도록 하고 (subsampling part가 pooling layer에 해당한다) 가장 왼쪽의 image data의 일부분에 해당하는 patch만 다음 hidden layer의 한 unit에 연결하는 것이다. 이런 식으로 네트워크를 만들게 되면, patch size에 따라 다음 feature map의 size가 결정될 것이다. 예를 들어 100 by 100 이미지에서 5 by 5 patch를 사용해 convolution layer를 구축할 경우, 이 layer의 feature map은 96 by 96이 될 것이다.

CNN은 이런 sparse weight에 parameter sharing을 또 더하여 vision task에 최적화된 network를 learning하게 된다. Parameter를 share하게 되면 그러지 않는 것과 비교하여 보다 적은 parameter만을 가지게 되므로 model의 complexity가 줄어드는 효과가 있을 뿐 아니라, 각각의 patch마다 따로 필터를 learning하는 대신, 모든 patch에 동일한 필터를 적용하도록 강제하는 효과가 있다. CNN은 아래 그림과 같이 각각의 hidden node들이 같은 location에 대해 같은 weight를 가지도록 설정하여 모든 hidden node들이 각각 다른 patch에 대해 같은 filter를 처리하는 것과 같은 형태로 모델을 디자인한다.

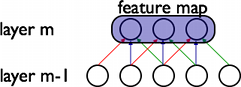
위 그림에서 같은 색으로 칠해진 edge는 서로 같은 weight를 가진다. 위 그림에서 볼 수 있듯, CNN은 fully connected layer를 가지지 않고, 그 sparse한 weight들에서도 서로 weight를 공유하도록 설정되어있다. 그렇지 않은 네트워크와 비교해보면 다음과 같다.

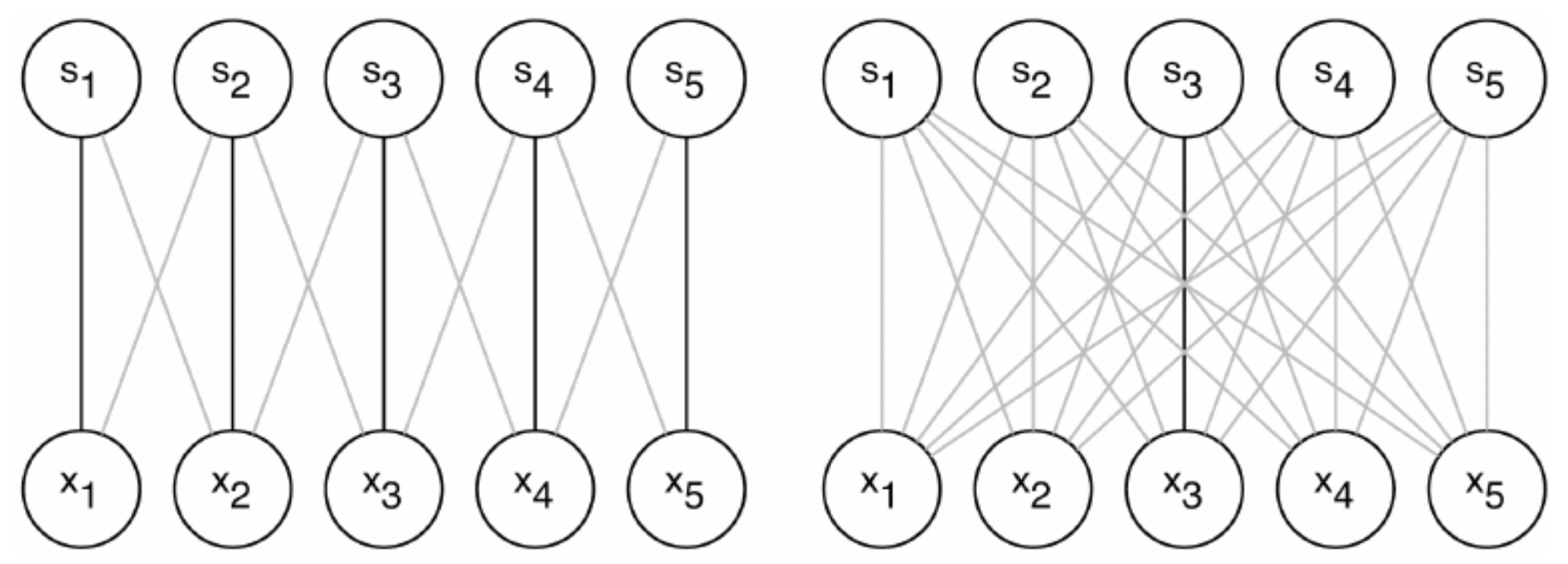
각각의 그림에서 검은색으로 연결된 edge들은 서로 같은 parameter를 가진다. 즉, 왼쪽은 한 번에 5개의 edge가 같은 weight를 가지지만, 오른쪽은 하나의 parameter로 한 개의 edge만 표현할 수 있다. 이렇게 표현하게 되면 convolution layer operation이 간단한 matrix multiplication으로 주어지게 되어 gradient를 계산하기 한 층 더 수월해진다는 장점도 존재한다. 자세한 내용은 algorithm 쪽에서 다루도록 하자.

마지막으로 equivalent representations는 위와 같은 sparse weight와 tied weight를 어떤 특정한 형태로 효율적으로 배치하게 되었을 때, 주어진 input의 변화에 대해 output이 변화하는 방식이 equivariant해지는 현상을 의미한다 (equivalent가 아니다). 예를 들어 function $f$가 function $g$와 equivariant하다는 의미는, $f(g(x)) = g(f(x))$인 경우를 말한다. 이미지 처리를 예로 들면 $g$는 임의의 linear transform이라고 할 수 있다. Shift, rotate, scale등의 image에 대한 transform들이 그것인데, 우리는 같은 이미지가 돌아가거나 움직이거나 살짝 scale되더라도 그 이미지가 어떤 이미지인지 잘 판별할 수 있지만, 컴퓨터에게는 그런 transform이 픽셀 값이 완전히 바뀌는 결과를 낳기 때문에 어떤 정보인지 판별하기 어려운 것이다. 그런데 만약 우리가 어떤 transform $g$에 대해 equivariant representation을 만들어내는 network $f$를 만들 수 있다면, input이 shift되거나 rotate되더라도 항상 적절한 representation을 가지도록 할 수 있을 것이다. (실제 CNN은 shift에만 equivariant하다.)

즉, 앞에서 shared parameter가 각각의 patch에 대해 같은 filter를 처리하는 것 처럼 설정하였기 때문에, 만약 image가 shift되더라도 feature map의 형태가 크게 뒤틀리는 것이 아니라, feature map도 image와 함께 shift되는 형태를 보이게 될 것이다.

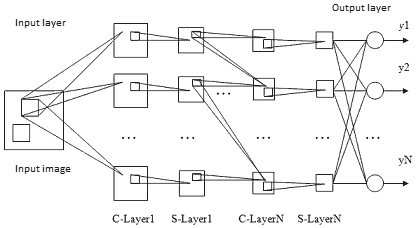
그런데 실제로는 한 image에 한 개의 filter가 아니라 여러 개의 filter가 필요할 수도 있다. 앞에서 설명한 convolution layer는 한 개의 convolution filter를 표현할 뿐이지만, 실제로는 이런 convolution filter가 한 개가 아니라 여러 개 만든 다음 그 값들을 concate하여 feature map을 표현해야할 수도 있다. 그렇기 때문에 실제로 CNN model은 한 개의 convolution layer가 아니라 아래와 같이 여러 개의 convolution layer가 결합된 꼴을 하고 있다. 참고로 공식적으로는 각각의 layer 혹은 filter를 kernel이라 하고, 그 kernel들이 모여있는 것을 한 layer로 부른다. (출처)

Convolutional Neural Network (CNN): Pooling Layer

Convolution Layer만 여러 개 연결하여 deep network를 구성하는 것도 가능하지만, 실제로는 더 dimension이 낮은 feature map을 얻기 위하여 subsampling이라는 것을 하게 된다. 앞에서 예로 들었던 것처럼 100 by 100 이미지에 5 by 5 convoltion patch size를 가지는 convolution layer를 연결할 경우 feature map의 size는 96 by 96이 되는데, 사실 이 96 by 96 feature map은 서로 매우 highly correlated 되어있는 값이 것이다. 특히 서로 이웃해있을수록 겹치는 영역이 많기 때문에 거의 비슷한 값을 가질 것이라고 예상할 수 있다. 아래 그림을 보자.

이미 앞에서 나왔던 그림이지만 설명을 위하여 다시 가져왔다. Pooling layer는 convolution layer의 feature map을 조금 더 줄여주는 역할을 한다. 전체 feature map을 그대로 들고가는 대신, 예를 들어 96 by 96 image feature map을 2 by 2 patch들로 쪼개는 것이다. 이렇게 할 경우 총 48 by 48 개의 output이 생기게 될텐데, subsampling이라는 것은 각각의 2 by 2 patch는 max, average 등의 operation을 행하는 것을 의미한다. 보통 max operation을 사용하고, 이 경우 간단하게 max pooling을 사용한다 라고 이야기 한다. 가끔 average pooling을 사용하는 경우도 있지만 보통 classification을 위한 모델들은 max pooling을 사용하니 참고하면 좋을 것 같다.

CNN은 이렇게 convolution layer와 pooling layer가 결합된 형태로 deep 하게 구성이 된다. 개인적으로 아래 그림이 CNN의 convolution layer와 max pooling layer를 잘 표현하는 그림이라고 생각한다. (출처)

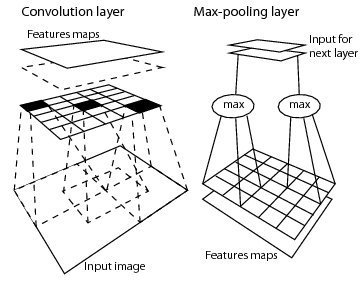
Convolutional Neural Network (CNN): Backpropagation

CNN의 기본 model은 알았으니 이제 이 network의 parameter를 어떻게 learning해야할지 알아보자. 기본적인 update algorithm은 이전 글에서 설명했던 backpropagation algorithm을 사용한다.

먼저 간단한 max pooling layer 부터 살펴보자. Pooling layer는 아래 p by q size의 patch 중에서 max 값을 선택하는 layer이다. 때문에 이를 수식으로 표현해보면 다음과 같이 쓸 수 있다. $(x,y)$는 pooling layer feature map의 x,y좌표를 나타내고, ($h_l$은 l번째 layer의 hidden variable들)

$$h_{l+1} (x, y) = max_{a-p\leq a\leq a+p, b-q\leq b\leq b+q}(h_l (x+a, y+b))$$

Parameter는 없으므로 $\frac{\partial h_{l+1} }{\partial h_{l}}$만 계산하면 된다. 이 경우 주어진 $(x,y)$가 만약 max pooling을 통해 선택된 값이라면 값을 그대로 passing하고, 만약 선택되지 않은 값이라면 0을 할당하면 된다.

Convolution layer는 operation이 꽤 복잡한데, 먼저 아래 그림을 보자.

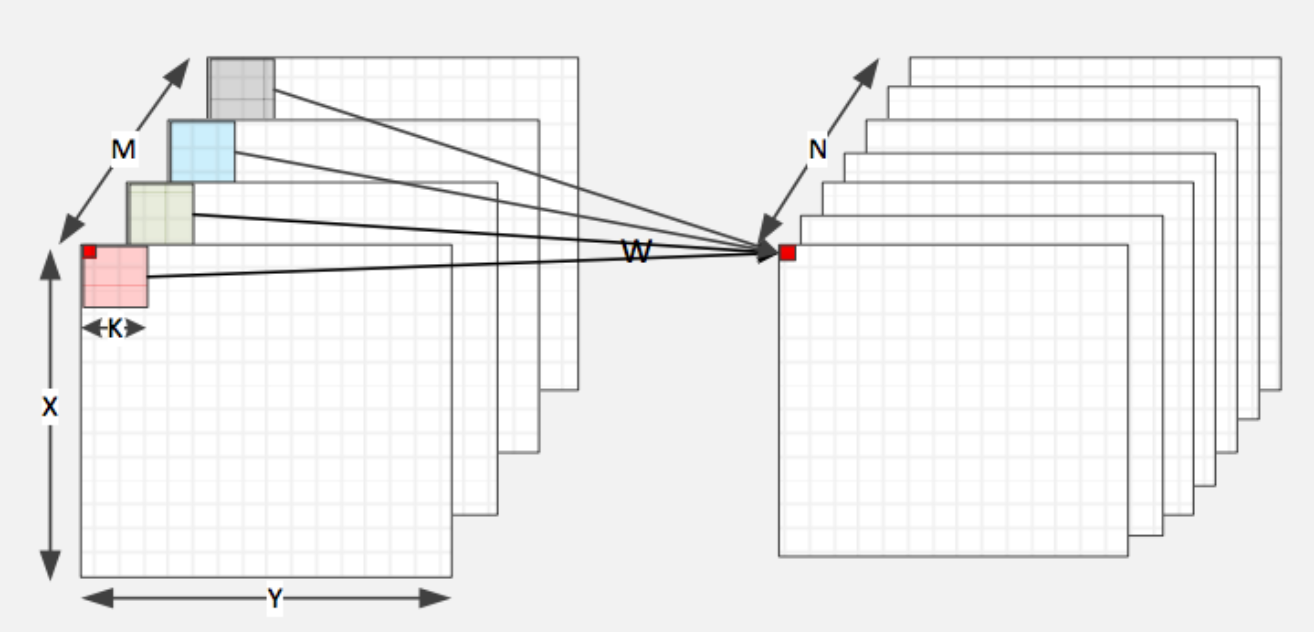
이때 l+1 번째 layer 중에서 i 번째 convolution filter의 x,y 좌표 값은 아래와 같이 표현된다. 아래 conv layer의 kernel은 m 개, 위 conv layer의 kernel은 n개 라고 해보자.

$$h_{l+1}(i, x,y) = \sum_{j=1}^m \sum_{a=1}^p \sum_{b=1}^q h_l (j, x+a, y+b) * w(i,n;a,b)$$

값이 좀 많이 복잡하긴 한데, 미분 값을 계산해보면, parameter의 gradient는 $\frac{E}{\partial w} = \sum_x \sum_y \frac{E}{h_{l+1} } (x,y) h_l (x,y)$와 같이 바로 전 layer의 pixel값에 대해 gradient 값을 곱한 것을 전부 더한 형태로 구할 수 있고, $\frac{E}{\partial h_l} $은 weight w로 이전 layer의 gradient를 convolution한 것들을 전부 더한 것과 같은 결과를 얻게 된다.

CNN의 모든 operation들은 단순 연산이 많고 branch가 없기 때문에 core가 많고, 모든 core가 하나의 operation pointer를 공유하는 GPU를 사용해 효율적으로 parallization하기 좋다. 보통 CNN은 caffe라는 C++ library를 사용해 learning하기 때문에 위에서 언급한 알고리즘을 실제로 구현할 일은 많지 않을 것 같다.

정리

Deep learning은 neural network의 layer를 deep 하게 쌓은 것에 지나지 않지만, 아무것도 하지 않고 layer를 깊게 쌓기만하면 overfitting이 너무 강하게 발생하여 제대로 된 결과를 얻을 수 없다. 이 글에서는 두 가지 overfitting을 피하는 방법을 설명하였다. 첫 번째 DBN은 주어진 network를 DBN이라는 RBM이 stack으로 쌓여있는 graphical probabilistic model로 표현한다. 그리고 주어진 데이터에 대해 likelihood를 maximize하는 parameter를 찾아서 그 값을 initial point로 사용해 gradient descent를 실행한다. 이때 RBM의 gradient 값을 정확히 구하는 것이 힘들기 때문에 Gibbs sampling의 iteration을 converge할때까지 돌리는 대신 한 번만 돌리는 Contrastive Divergence 알고리즘이 제안된다. DBN은 RBM을 layer wise greedy update rule을 통해 parameter를 update하게 된다.

두 번째로 설명한 CNN은 sparse weight, tied weight, equivariant representation이라는 세 가지 아이디어를 기반으로 모델의 complexity는 최소화하면서 vision에 최적화되어있는 형태의 모델이다. Parameter update는 backpropagation으로 하게 되는데, 보통 구현되어있는 툴을 사용하게 되므로 세부 update rule을 직접 구현할 일은 많지 않을 것 같다.

이 밖에 regularization이나 optimization method들과 같이 deep learning과 관련된 중요한 개념들 역시 추후 다른 포스트를 통해 소개할 수 있도록 하겠다.

Reference

변경 이력

  • 2015년 9월 21일: 글 등록
  • 2015년 10월 31일: 오타 수정

Machine Learning 스터디의 다른 글들