README   SanghyukChun's Blog

Machine Learning 스터디 (13) Clustering (K-means, Gaussian Mixture Model)

| Comments

들어가며

첫 번째 글에서 설명했던 것 처럼 Machine Learning은 크게 Supervised Learning, Unsupervised Learning 그리고 Reinforcement Learning으로 구분된다. 앞서 이미 그 중 Supervised Learning을 간략하게 다룬 글이 있었고, 이 글에서는 그 중 Unsupervised Learning의 가장 대표적인 예시인 Clustering 대해 다룰 것이며 가장 대표적이고 간단한 두 가지 알고리즘에 대해서 역시 다룰 것이다.

What is Clustering?

Clustering은 Unsupervised Learning의 일종으로, label 데이터 없이 주어진 데이터들을 가장 잘 설명하는 cluster를 찾는 문제이다. 왜 클러스터링이 필요할까? Classification을 하기 위해서는 데이터와 각각의 데이터의 label이 필요하지만, 실제로는 데이터는 존재하지만 그 데이터의 label이나 category가 무엇인지 알 수 없는 경우가 많기 때문에 classfication이 아닌 다른 방법을 통해 데이터들을 설명해야하는 경우가 발생한다. 아래 그림은 클러스터링이 어떤 것인지 잘 보여주는 그림이다.

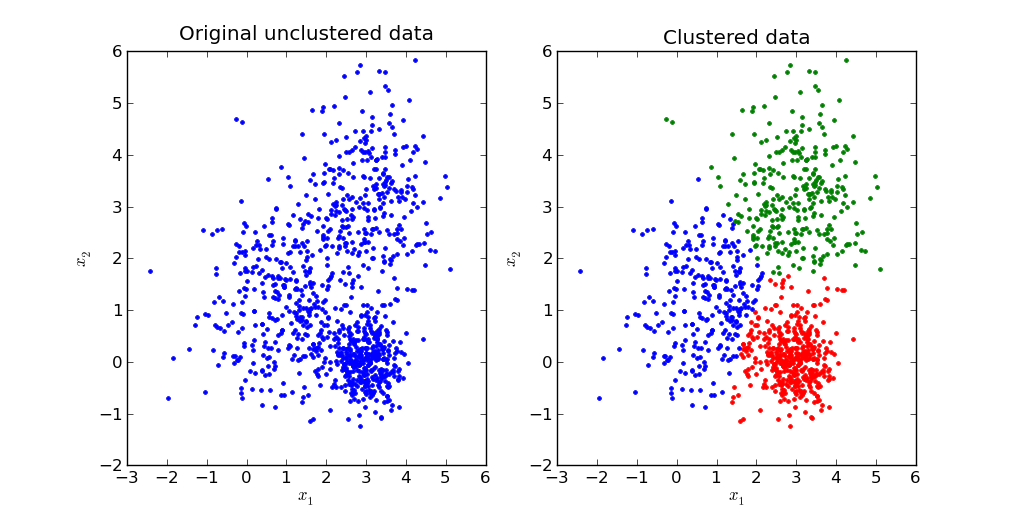
우리에게 처음 주어진 것은 왼쪽 파란 데이터이다. 각각의 데이터에 대한 정보는 아무 것도 없는 상태에서 주어진 데이터들을 가장 잘 설명하는 클러스터를 찾아내는 것이 클러스터링의 목적이다. 따라서 클러스터링은 대부분 Optimization 문제를 푸는 경우가 많다. 이는 클러스터링 뿐 아니라 다른 많은 unsupervised learning에서도 역시 마찬가지이다.

첫 번째 글과 이전 글에서 머신러닝 문제는 먼저 주어진 데이터에 대한 가정을 하고, 해당 가정을 만족하는 best hypothesis를 찾는 문제라고 언급한 적이 있다. Clustering 문제 역시 Machine Learning 문제이므로 데이터에 대한 가정을 먼저 해야하고, best hypothesis를 찾는 과정을 거친다. 따라서 각각의 서로 다른 clustering algorithm들은 서로 다른 assumption을 가지고 있으며, 해당 assumption을 가장 잘 만족하는 function parameter를 계산하는 과정이다. 앞으로 설명하게 될 알고리즘들에 대한 설명을 읽을 때 데이터에 대해 어떤 가정을 하였는지 꼼꼼히 확인하면서 읽으면 알고리즘을 이해하기 한결 수월할 것이다.

K-means

클러스터를 정의하는 방법에는 여러 가지가 있을 수 있지만, 가장 간단한 정의 중 하나는 클러스터 내부에 속한 데이터들이 서로 ‘가깝다’라고 정의하고, ‘가장 가까운’ 내부 거리를 가지는 클러스터를 고르는 것이다. K-means는 같은 클러스터에 속한 데이터는 서로 ‘가깝다’ 라고 가정한다. 이때 각각의 클러스터마다 ‘중심’이 하나씩 존재하고, 각각의 데이터가 그 중심과 ‘얼마나 가까운가’를 cost로 정의한다. K-means는 이렇게 정의된 cost를 가장 줄이는 클러스터를 찾는 알고리즘이다. 수식으로 적으면 다음과 같다.

$$ \min_{b,w} \sum_i^n \sum_j^k w_{ij} \| x_i - b_j \|_2^2 \text{ s.t. } \sum_j w_{ij} = 1, \forall j$$

데이터는 $n$개 있으며 클러스터는 $k$개 있다고 가정했다. 이때, $b_j$는 $j$ 번째 클러스터의 ‘중심’을 의미하며, $w_{ij}$는 $i$ 번째 데이터가 $j$ 번째 클러스터에 속하면 1, 아니면 0을 가지는 binary variable이다. 또한 뒤에 붙는 조건은 반드시 각 데이터 별로 한 개의 클러스터에 assign이 되어야한다는 constraint이다.

이 문제는 풀기 쉬운 문제가 아니다. Binary variable $w_{ij}$ 때문에, 모든 cluster 조합을 하나하나 확인해야만 optimal한 값을 구할 수 있다. 즉, jointly optimize하는 것이 매우 어렵다. 그러나 재미있게도 $b$와 $w$ 둘 중 하나를 고정하고 나머지 하나를 update하는 것은 매우 간단하다. 나머지 값이 고정되었을 때 $b_j$의 optimal값은 $j$ 번째 클러스터의 ‘mean’을 계산하는 것이다 (이 때문에 ‘$k$’ 개의 ‘mean’을 찾는다고 해서 k-means 알고리즘이다). $w_{ij}$의 optimal 값은 모든 데이터 i에 대해, 각각 모든 클러스터 중에서 $x_i - b_j$가 가장 작은 클러스터에 assign하는 것이 optimal한 solution이다. 이렇듯 만약 다른 변수 하나를 정확하게 알고 있다고 생각하면 아주 간단한 방법으로 alternative optimization이 가능하다. 사실 이 개념은 예전에 적은 convex optimization글에서 잠깐 언급했던 coordinate descent 방법과 거의 유사하다. K-means 알고리즘은 이렇게 $b$와 $w$를 alternative하게 계속 update하면서 $b$와 $w$가 더 이상 바뀌지 않을 때 까지 계산을 반복하는 알고리즘이다. 안타깝게도 K-means는 global optimum에 수렴하지 않고 local한 optimum에 수렴하므로 initialization에 매우매우 취약하다는 단점이 존재한다.

또한 여담으로 K-means objective function에 사용한 $\ell_2$ norm의 제곱이 outlier 혹은 noise에 매우 취약하기 때문에 조금 더 outlier에 덜 sensitive한 ‘robust한’ norm을 사용하는 방법도 존재한다. 예를 들어 $\ell_2$ norm의 제곱을 $\ell_1$ norm으로 바꾸면 ‘mean’ 대신에 ‘median’을 찾는 문제로 바뀌게 된다. 이를 k-median이라고 부른다. 그 밖에도 k-means의 robustness를 개선하기 위한 다양한 방법들이 개발이 되어있지만 이 글에서는 다루지 않도록 하겠다.

Gaussian Mixture Model

K-means algorithm의 key idea는 ‘alternative update’이다. 즉, coordinate wise로 다른 변수들을 고정한 채로 ‘alternative’하게 변수들을 update함으로써 jointly optimization을 할 수 없는 문제를 푸는 것이다. 비록 그 결과가 global하지 않은 local에 converge하더라도, 찾지 못하는 것보다는 훨씬 낫기 때문에 실제로 이런 방법이 많이 쓰인다. 이번 섹션에서는 이런 방법을 사용하는 또 다른 알고리즘을 하나 소개하도록 하겠다.

Gaussian Mixture Model, Mixture of Gaussian, GMM, 혹은 MoG는 데이터가 ‘Gaussian’의 ‘Mixture’로 구성이 되어있다고 가정한다. 보통 GMM이라고 많이 부르며, 이 글에서 다루는 GMM은 가장 optimal한 GMM을 찾는 알고리즘을 의미한다. 즉, 데이터가 $k$개의 gaussian으로 구성되어있다고 했을 때, 가장 데이터를 잘 설명하는 $k$개의 평균과 covariance를 찾는 알고리즘이다. 아래 그림은 3개의 gaussian으로 구성되어있다고 가정하고 그 gaussian 분포들을 찾은 결과이다.

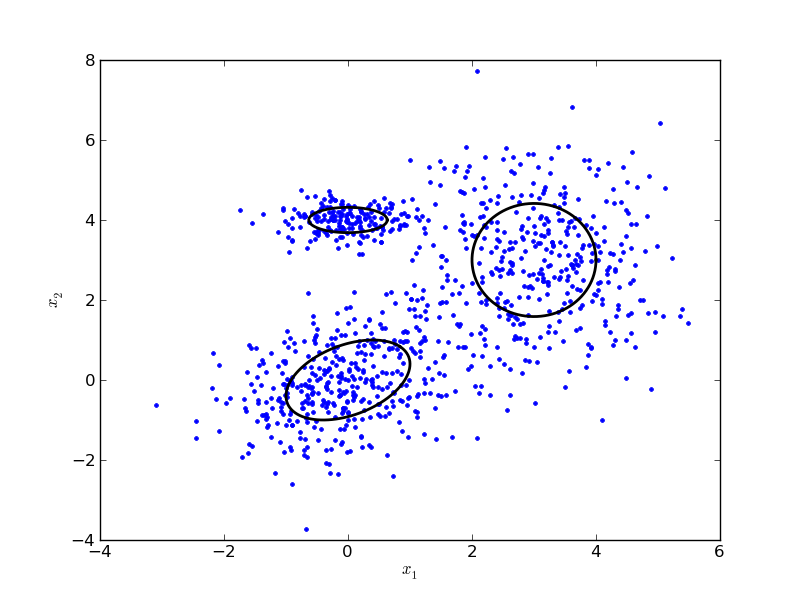
모든 machine learning 문제는 ‘performance measure’를 가진다고 예전에 얘기한 적이 있다. GMM의 performance measure는 log likelihood function이다. 즉, 주어진 paramter에 대해 데이터 X의 확률을 가장 크게 만드는 parameter를 찾는 것이 목표가 된다. log likelihood는 $\ln p(X|\theta)$로 정의가 된다. 우리가 찾아야하는 parameter $\theta$는 각각의 gaussian의 평균 $\mu_j$, covariance $\Sigma_j$, 그리고 마지막으로 각각의 데이터가 각각의 gaussian에 속할 확률 $\pi_j$로 구성된다. 따라서 주어진 $\mu_j, \Sigma_j$에 대한 $x_i$의 multinomial gaussian distribution을 $N(x_i|\mu_j, \Sigma_j)$라고 정의한다면 log likelihood function은 다음과 같이 기술할 수 있다.

$$ \ln p(X|\pi, \mu, \Sigma) = \sum_i^n \ln \sum_j^k \pi_j N (x_i | \mu_j, \Sigma_j) $$

그러나 역시 이 문제도 jointly update가 매우매우 어려운 문제이다. 그러나 K-means와 비슷하게도 $\pi$를 고정하고 $\mu, \Sigma$를 계산하는 것은 쉬우며, 그 반대 역시 쉽다. 따라서 비슷하게 alternative update를 통해 문제를 해결하는 알고리즘을 어렵지 않게 디자인 할 수 있다. 역시 이 알고리즘도 global로 수렴하지 않고 local로만 수렴하게 된다. GMM을 풀기 위해서 사용되는 알고리즘 중 가장 유명한 알고리즘으로는 ‘EM’ 알고리즘이 존재한다. 이 알고리즘에 대해서는 다음 글에서 더 자세하게 설명하도록 하고, 이 글에서는 EM 알고리즘이라는 것을 알고 있는 상태에서 어떻게 각 step을 해결할 수 있는지에 대해서만 다루도록 하겠다. E-step에서는 현재 주어진 $\mu, \Sigma, \pi$들을 사용해 가장 ‘expectation’이 높은 latent variable의 값을 찾아내며, M-step에서는 새로 estimate된 latent variable을 사용해 그 값을 maximize하는 $\mu, \Sigma, \pi$를 찾는다. EM 알고리즘은 E-step과 M-step이 계속 번갈아 진행되며, 더 이상 값이 변하지 않을 때 까지 반복된다. K-means를 이런 관점으로 바라보게 된다면, cluster information $w_{ij}$를 update하는 과정이 E-step, $b$를 update하는 과정을 M-step이라고 할 수 있다. (그러나 K-means을 푸는 알고리즘은 엄밀하게 말하면 EM 알고리즘이 아니다)

사실 엄밀하게 설명하면 GMM을 푸는 EM에서 E-step 때 update하는 것은 정확하게 $\pi$와 같은 것은 아니다. EM으로 이 문제를 풀기 위해서 우리는 새로운 ‘latent’ variable을 introduce해야한다. latent variable은 쉽게 생각하면 graphical model에서 hidden variable에 해당하는 값이다. 다음에 EM 알고리즘에 대해 자세히 다룰 때 다시 설명하겠지만, 이렇게 latent variable을 설정하는 이유는 어떤 특정 variable의 marginal distribution을 optimize하는 것은 어려울 때, latent variable을 사용해 그 variable과 latent variable의 joint distribution을 다루는 것은 간단할 수 있기 때문이다. GMM에서는 latent variable $z$를 introduce하게 된다. $z$는 $k$-ary variable로, $z$의 $j$ 번째 dimension인 $z_j$는 Binary random variable이며, $p(z_j=1) = pi_j, $ where $\sum_j z_j = 1$ and $\sum_j \pi_j = 1$ 이라는 조건을 가지고 있다. $z$의 marginal probability는 $p(z) = \prod_j \pi_j^{z_j}$로 어렵지 않게 계산할 수 있으며, 비슷하게 주어진 데이터 $x$에 대한 conditional distribution 역시 간단하게 다음과 같이 표현된다. $p(x|z) = \prod_j N(x|\mu_j, \Sigma_j)^{z_j}$.

따라서 앞선 식들로부터 joint distribution을 얻을 수 있고, 그 값을 marginalize해 다음과 같은 결과를 얻을 수 있다.

$$ p(x) = \sum_z p(x,z) = \sum_z p(z)p(x|z) = \sum_j \pi_j N(x|\mu_j, \Sigma_j) $$

정리하자면, 각각의 data point $x_i$ in GMM의 graphical representation은 다음과 같이 표현할 수 있다.

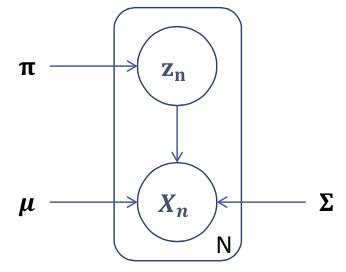
위의 결과들을 토대로 이제 간단하게 EM algorithm을 돌릴 수 있다. 먼저 E step에서는 $p(z_j = 1|x)$를 계산할 것이다. 각 데이터에 대해 $j$ 번째 클러스터에 속할 확률, 혹은 posterior를 계산하는 과정이다. 이 값은 Bayes rule을 통해 간단하게 다음과 같이 계산할 수 있다.

$$ p(z_j = 1|x) = \frac{p(z_j=1)p(x|z_j=1)}{\sum_j^k p(z_j=1)p(x|z_j=1)} = \frac{\pi_j N(x|\mu_j, \Sigma_j)}{\sum_j^k \pi_j N(x|\mu_j \Sigma_j)} $$

다음으로 $z$를 fix했을 때 다음과 같이 나머지 paramter를 계산할 수 있다.

$$ \mu_j = \frac{1}{\sum_i p(z_j=1|x)} \sum_i p(z_{ij}=1|x) x_i$$

$$ \Sigma_j = \frac{1}{\sum_i p(z_j=1|x)} \sum_i p(z_{ij}=1|x) (x_i-\mu_j) (x_i-\mu_j)^\top$$

$$ \pi_j = \frac{\sum_i p(z_j=1|x)}{N}$$

정리하자면, GMM을 풀기 위한 EM 알고리즘은, 먼저 각각의 데이터가 어느 클러스터에 속할지에 대한 정보를 update해 ($z$를 업데이트 하여) expectation을 계산하고, 다음으로 업데이트 된 정보들을 사용해 나머지 값들로 가장 log likelihood를 최대화하는 parameter들을 ($\mu, \Sigma, \pi$를) 찾아낸다. 알고리즘을 돌리면 아래처럼 iteration이 지날 때 마다 점점 좋은 값을 찾아준다. (출처: Geometry & Recognition :: Gaussian Mixture Model & K-means)

EM 알고리즘에 대한 심도있는 이해 없이 이 글을 이해하는 것은 조금 어려울 수 있다. 이 글이 잘 이해가 되지 않는다면 먼저 EM 알고리즘에 대해 설명한 다음 글을 읽어본 다음 다시 읽어보기를 권한다.

정리

Clustering은 unsupervised learning 분야에서 가장 활발히 연구되는 분야 중 하나이다. 이 글에서는 여러 종류의 클러스터링 알고리즘 중에서 optimization function을 (1) 거리 기반으로 세우고 그것을 푸는 알고리즘과 (2) 확률과 확률분포를 기반으로 세우고 그것을 푸는 알고리즘을 소개하였다. 특히 GMM은 다음 글에서 다룰 주제인 EM algorithm과 밀접하게 관련되는 내용이므로 한 번 쯤은 책이나 렉쳐노트를 정독하는 것을 권한다.

변경 이력

  • 2015년 3월 25일: 글 등록
  • 2015년 6월 14일: EM 알고리즘 링크 추가 및 설명 변경

Reference

Machine Learning 스터디의 다른 글들