들어가며
최근 Machine Learning 분야에서 가장 뜨거운 분야는 누가 뭐래도 Deep Learning이다. 엄청나게 많은 사람들이 관심을 가지고 있고, 공부하고 응용하고 있지만, 체계적으로 공부할 수 있는 자료가 많이 없다는 것이 개인적으로 조금 안타깝다. 이제 막 각광받기 시작한지 10년 정도 지났고, 매년 새로운 자료들이 쏟아져나오기 때문에 책이나 정리된 글을 찾기가 쉽지가 않다. 그러나 Deep Learning은 결국 artificial neural network를 조금 더 복잡하게 만들어놓은 모델이고, 기본적인 neural network에 대한 이해만 뒷받침된다면 자세한 내용들은 천천히 탑을 쌓는 것이 가능하다고 생각한다. 이 글에서는 neural network의 가장 기본적인 model에 대해 다루고, model paramter를 update하는 algorithm인 backpropagation에 대해서 다룰 것이다. 조금 더 advanced한 topic들은 이 다음 글에서 다룰 예정이다. 이 글의 일부 문단은 이전 글들을 참고하였다.
Motivation of Neural Network
이름에서부터 알 수 있듯 neural network는 사람의 뇌를 본 따서 만든 머신러닝 모델이다 (참고: 원래 neural network의 full name은 artificial neural network이지만, 일반적으로 neural network라고 줄여서 부른다). 본격적으로 neural network에 대해 설명을 시작하기 전에 먼저 인간보다 컴퓨터가 훨씬 잘 할 수 있는 일들이 무엇이 있을지 생각해보자.
- 1부터 10000000까지 숫자 더하기
- 19312812931이 소수인지 아닌지 판별하기
- 주어진 10000 by 10000 matrix 의 determinant값 계산하기
- 800 페이지 짜리 책에서 ‘컴퓨터’ 라는 단어가 몇 번 나오는지 세기
반면 인간이 컴퓨터보다 훨씬 잘 할 수 있는 일들에 대해 생각해보자
- 다른 사람과 상대방이 말하고자하는 바를 완벽하게 이해하면서 내가 하고 싶은 말을 상대도 이해할 수 있도록 전달하기
- 주어진 사진이 고양이 사진인지 강아지 사진인지 판별하기
- 사진으로 찍어보낸 문서 읽고 이해하기
- 주어진 사진에서 얼마나 많은 물체가 있는지 세고, 사진에 직접 표시하기
컴퓨터가 잘 할 수 있는 0과 1로 이루어진 사칙연산이다. 기술의 발달로 인해 지금은 컴퓨터가 예전보다도 더 빠른 시간에, 그리고 더 적은 전력으로 훨씬 더 많은 사칙연산을 처리할 수 있다. 반면 사람은 사칙연산을 컴퓨터만큼 빠르게 할 수 없다. 인간의 뇌는 오직 빠른 사칙연산만을 처리하기 위해 만들어진 것이 아니기 때문이다. 그러나 인지, 자연어처리 등의 그 이상의 무언가를 처리하기 위해서는 사칙연산 그 너머의 것들을 할 수 있어야하지만 현재 컴퓨터로는 인간의 뇌가 할 수 있는 수준으로 그런 것들을 처리할 수 없다.
예를 들어 아래와 같이 주어진 사진에서 각각의 물체를 찾아내는 문제를 생각해보자 (출처: 링크). 사람에게는 너무나 간단한 일이지만, 컴퓨터가 처리하기에는 너무나 어려운 일이다. 어떻게 어디부터 어디까지가 ‘tv or monitor’라고 판단할 수 있을까? 컴퓨터에게 사진은 단순한 0과 1로 이루어진 픽셀 데이터에 지나지 않기 때문에 이는 아주 어려운 일이다.
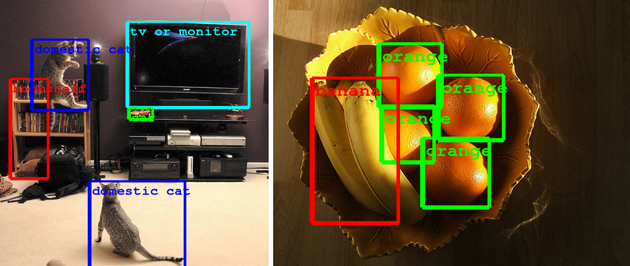
그렇기 때문에 자연언어처리, 컴퓨터 비전 등의 영역에서는 인간과 비슷한 성능을 내는 시스템을 만들 수만 있다면 엄청난 기술적 진보가 일어날 수 있을 것이다. 그렇기 때문에 인간의 능력을 쫓아가는 것 이전에, 먼저 인간의 뇌를 모방해보자라는 아이디어를 낼 수 있을 것이다. Neural Network는 이런 모티베이션으로 만들어진 간단한 수학적 모델이다. 우리는 이미 인간의 뇌가 엄청나게 많은 뉴런들과 그것들을 연결하는 시냅스로 구성되어있다는 사실을 알고 있다. 또한 각각의 뉴런들이 activate되는 방식에 따라서 다른 뉴런들도 activate 되거나 activate되지 않거나 하는 등의 action을 취하게 될 것이다. 그렇다면 이 사실들을 기반으로 다음과 같은 간단한 수학적 모델을 정의하는 것이 가능하다.
Model of Neural Network: neuron, synapse, activation function
먼저 뉴런들이 node이고, 그 뉴런들을 연결하는 시냅스가 edge인 네트워크를 만드는 것이 가능하다. 각각의 시냅스의 중요도가 다를 수 있으므로 edge마다 weight를 따로 정의하게 되면 아래 그림과 같은 형태로 네트워크를 만들 수 있다. (출처: 위키)
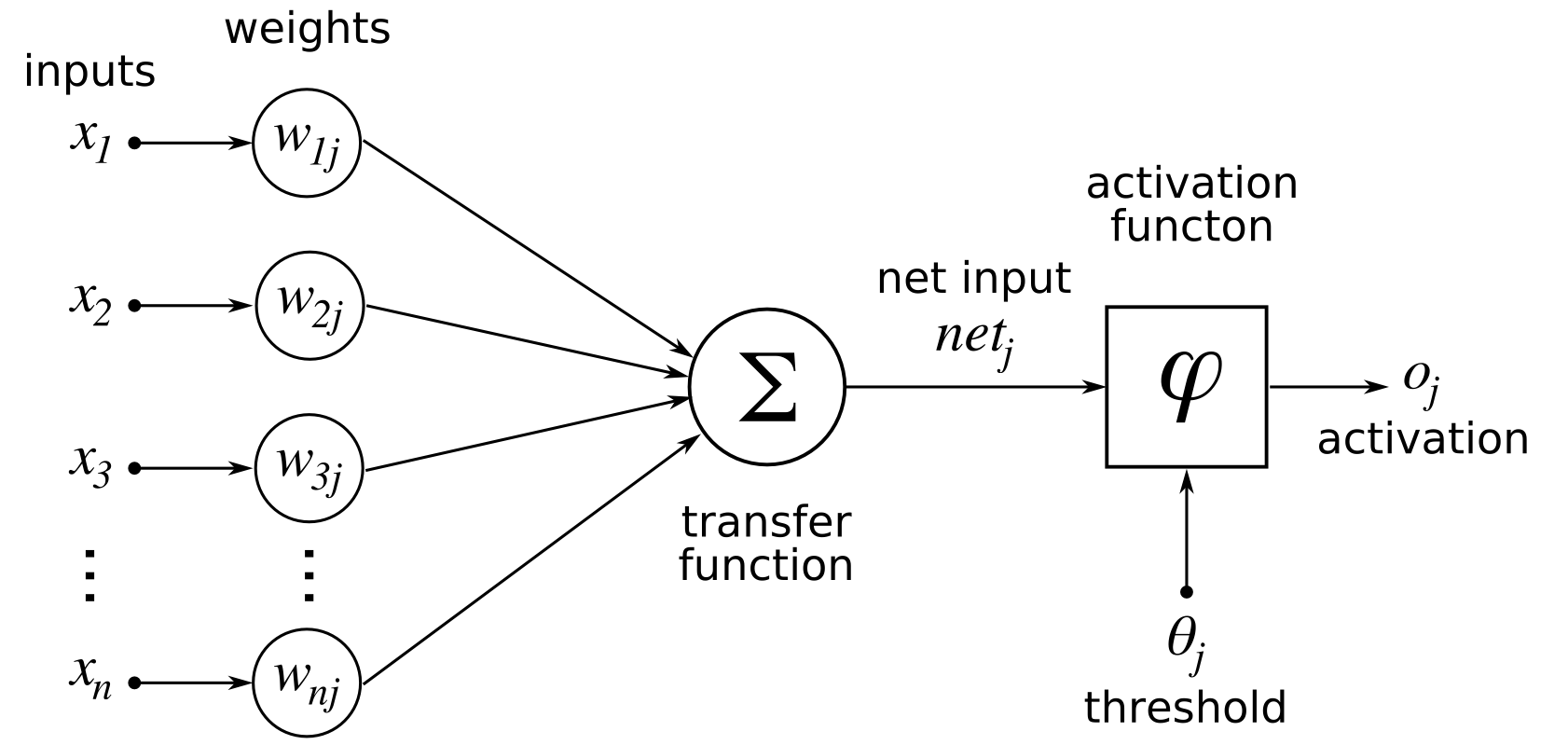
보통 neural network는 directed graph이다. 즉, information propagation이 한 방향으로 고정된다는 뜻이다. 만약 undirected edge를 가지게 되면, 혹은 동일한 directed edge가 양방향으로 주어질 경우, information propagation이 recursive하게 일어나서 결과가 조금 복잡해진다. 이런 경우를 recurrent neural network (RNN)이라고 하는데, 과거 데이터를 저장하는 효과가 있기 때문에 최근 음성인식 등의 sequencial data를 처리할 때 많이 사용되고 있다. 이번 ICML 2015에서도 RNN 논문이 많이 발표되고 있고, 최근들어 연구가 활발한 분야이다. 이 글에서는 일단 가장 간단한 ‘multi layer perceptron (MLP)’라는 구조만 다룰 것인데, 이 구조는 directed simple graph이고, 같은 layer들 안에서는 서로 connection이 없다. 즉, self-loop와 parallel edge가 없고, layer와 layer 사이에만 edge가 존재하며, 서로 인접한 layer끼리만 edge를 가진다. 즉, 첫번째 layer와 네번째 layer를 직접 연결하는 edge가 없는 것이다. 앞으로 layer에 대한 특별한 언급이 없다면 이런 MLP라고 생각하면 된다. 참고로 이 경우 information progation이 ‘forward’로만 일어나기 때문에 이런 네트워크를 feed-forward network라고 부르기도 한다.
다시 일반적인 neural network에 대해 생각해보자. 실제 뇌에서는 각기 다른 뉴런들이 activate되고, 그 결과가 다음 뉴런으로 전달되고 또 그 결과가 전달되면서 최종 결정을 내리는 뉴런이 activate되는 방식에 따라 정보를 처리하게 된다. 이 방식을 수학적 모델로 바꿔서 생각해보면, input 데이터들에 대한 activation 조건을 function으로 표현하는 것이 가능할 것이다. 이것을 activate function이라고 정의한다. 가장 간단한 activation function의 예시는 들어오는 모든 input 값을 더한 다음, threshold를 설정하여 이 값이 특정 값을 넘으면 activate, 그 값을 넘지 못하면 deactivate되도록 하는 함수일 것이다. 일반적으로 많이 사용되는 여러 종류의 activate function이 존재하는데, 몇 가지를 소개해보도록 하겠다. 편의상 $t = \sum_i w_i * x_i$ 라고 정의하겠다. (참고로, 일반적으로는 weight 뿐 아니라 bais도 고려해야한다. 이 경우 $t = \sum_i (w_i * x_i + b_i) $로 표현이 되지만, 이 글에서는 bais는 weight와 거의 동일하기 때문에 무시하고 진행하도록 하겠다. - 예를 들어 항상 값이 1인 $x_0$를 추가한다면 $w_0$가 bais가 되므로, 가상의 input을 가정하고 weight와 bais를 동일하게 취급하여도 무방하다.)
sigmoid function: $f(t) = \frac{1}{1+ e^{-t}}$
tanh function: $f(t) = \frac{e^t - e^{-t}}{e^t + e^{-t} }$
absolute function: $f(t) = \|t\|$
ReLU function: $f(t) = max(0, t)$
보통 가장 많이 예시로 드는 activation function으로 sigmoid function이 있다. (출처는 위의 위키와 같음)
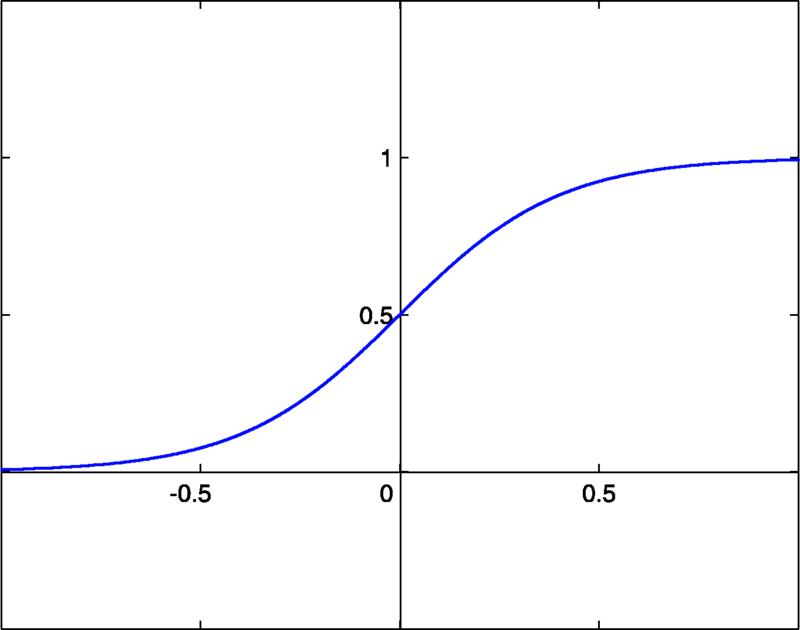
이 함수는 미분이 간단하다거나, 실제 뉴런들이 동작하는 것과 비슷하게 생겼다는 등의 이유로 과거에는 많이 사용되었지만, 별로 practical한 activation function은 아니고, 실제로는 ReLU를 가장 많이 사용한다 (2012년 ImageNet competition에서 우승했던 AlexNet publication을 보면, ReLU와 dropout을 쓰는 것이 그렇지 않은 것보다 훨씬 더 우수한 결과를 얻는다고 주장하고 있다. 이에 대한 자세한 내용은 다른 포스트를 통해 보충하도록 하겠다). 참고로 neuron을 non-linearity라고 부르기도 하는데, 그 이유는 activation function으로 linear function을 사용하게 되면 아무리 여러 neuron layer를 쌓는다고 하더라도 그것이 결국 하나의 layer로 표현이 되기 때문에 non-linear한 activation function을 사용하기 때문이다.
따라서 이 모델은 처음에 node와 edge로 이루어진 네트워크의 모양을 정의하고, 각 node 별 activation function을 정의한다. 이렇게 정해진 모델을 조절하는 parameter의 역할은 edge의 weight가 맡게되며, 가장 적절한 weight를 찾는 것이 이 수학적 모델을 train할 때의 목표가 될 것이다.
Inference via Neural Network
먼저 모든 paramter가 결정되었다고 가정하고 neural network가 어떻게 결과를 inference하는지 살펴보도록하자. Neural network는 먼저 주어진 input에 대해 다음 layer의 activation을 결정하고, 그것을 사용해 그 다음 layer의 activation을 결정한다. 이런 식으로 맨 마지막까지 결정을 하고 나서, 맨 마지막 decision layer의 결과를 보고 inference를 결정하는 것이다 (아래 그림 참고, 빨간 색이 activate된 뉴런이다).
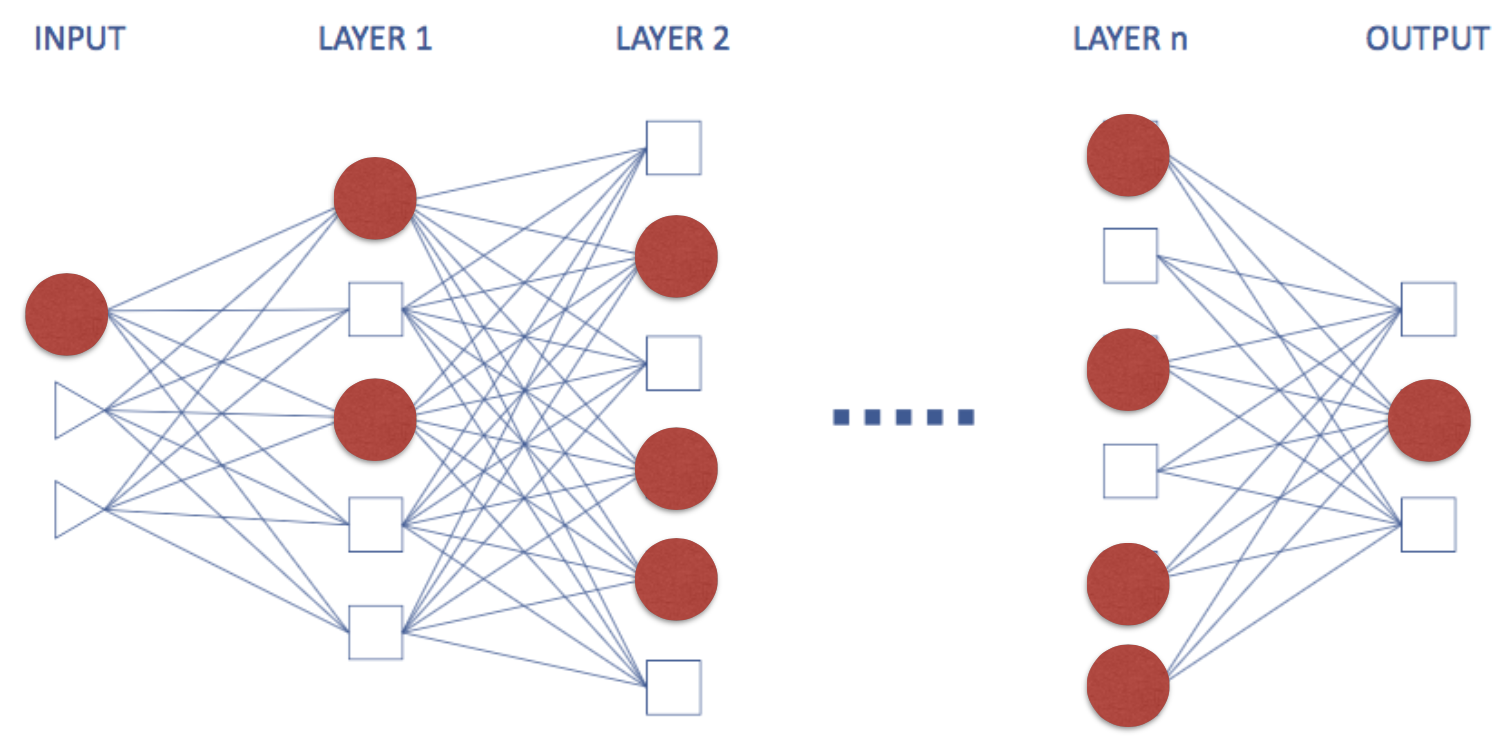
이때, classification이라고 한다면 마지막 layer에 내가 classification하고 싶은 class 개수만큼 decision node를 만든 다음 그 중 하나 activate되는 값을 선택하는 것이다. 예를 들어 0부터 9까지 손글씨 데이터를 (MNIST라는 유명한 dataset이 있다) classification해야한다고 생각해보자. 그 경우는 0부터 9까지 decision이 총 10개이므로 마지막 decision layer에는 10개의 neuron이 존재하게 되고 주어진 데이터에 대해 가장 activation된 크기가 큰 decision을 선택하는 것이다.
Backpropagation Algorithm
마지막으로 이제 weight를 어떻게 찾을 수 있는지 weight paramter를 찾는 알고리즘에 대해 알아보자. 먼저 한 가지 알아두어야 할 점은 activation function들이 non-linear하고, 이것들이 서로 layer를 이루면서 복잡하게 얽혀있기 때문에 neural network의 weight optimization이 non-convex optimization이라는 것이다. 따라서 일반적인 경우에 neural network의 paramter들의 global optimum을 찾는 것은 불가능하다. 그렇기 때문에 보통 gradient descent 방법을 사용하여 적당한 값까지 수렴시키는 방법을 사용하게 된다.
Neural network (이 글에서는 multi-layer feed-forward network)의 parameter를 update하기 위해서는 backpropagation algorithm이라는 것을 주로 사용하는데, 이는 단순히 neural network에서 gradient descent를 chain rule을 사용하여 단순화시킨 것에 지나지 않는다 (Gradient descent에 대해서는 이전에 쓴 Convex Optimization글에서 자세히 다루고 있으니 참고하면 좋을 것 같다). 모든 optimization 문제는 target function이 정의되어야 풀 수 있다. Neural network에서는 마지막 decision layer에서 우리가 실제로 원하는 target output과 현재 network가 produce한 estimated output끼리의 loss function을 계산하여 그 값을 minimize하는 방식을 취한다. 일반적으로 많이 선택하는 loss에는 다음과 같은 함수들이 있다. 이때 우리가 원하는 d-dimensional target output을 $t=[t_1, \ldots, t_d]$로, estimated output을 $x=[x_1, \ldots, x_d]$ 로 정의해보자.
sum of squares (Euclidean) loss: $\sum_{i=1}^d (x_i - t_i)^2 $
softmax loss: $-\sum_{i=1}^d \bigg[ t_i \log \big(\frac{e^{x_i} }{\sum_{j=1}^d e^{x_j} }\big) + (1 - t_i) \log \big(1 - \frac{e^{x_i} }{\sum_{j=1}^d e^{x_j} }\big) \bigg] $
cross entropy loss: $\sum_{i=1}^d [ -t_i \log x_i - (1-t_i) \log (1-x_i) ]$
hinge loss: $\max(0,1-t \cdot x)$, 이때 $\cdot$은 내적을 의미한다.
상황에 따라 조금씩 다른 loss function을 사용하지만, classification에 대해서는 보통 softmax loss가 gradient의 값이 numerically stable하기 때문에 softmax loss를 많이 사용한다. 이렇게 loss function이 주어진다면, 이 값을 주어진 paramter들에 대해 gradient를 구한 다음 그 값들을 사용해 parameter를 update하기만 하면 된다. 문제는, 일반적인 경우에 대해 이 paramter 계산이 엄청 쉬운 것만은 아니라는 것이다.
Backpropagtaion algorithm은 chain rule을 사용해 gradient 계산을 엄청 간단하게 만들어주는 알고리즘으로, 각각의 paramter의 grdient를 계산할 때 parallelization도 용이하고, 알고리즘 디자인만 조금 잘하면 memory도 많이 아낄 수 있기 때문에 실제 neural network update는 이 backpropagtaion 알고리즘을 사용하게 된다.
Gradient descent method를 사용하기 위해서는 현재 parameter에 대한 gradient를 계산해야하지만, 네트워크가 복잡해지면 그 값을 바로 계산하는 것이 엄청나게 어려워진다. 그 대신 backpropataion algorithm에서는 먼저 현재 paramter를 사용하여 loss를 계산하고, 각각의 parameter들이 해당 loss에 대해 얼마만큼의 영향을 미쳤는지 chain rule을 사용하여 계산하고, 그 값으로 update를 하는 방법이다. 따라서 backpropagation algorithm은 크게 두 가지 phase로 나눌 수가 있는데, 하나는 propagation phase이며, 하나는 weight update phase이다. propagation phase에서는 training input pattern에서부터 에러, 혹은 각 뉴런들의 변화량을 계산하며, weight update phase에서는 앞에서 계산한 값을 사용해 weight를 update시킨다.
Phase 1: Propagation
- Forward propagation: input training data로부터 output을 계산하고, 각 ouput neuron에서의 error를 계산한다. (input -> hidden -> output 으로 정보가 흘러가므로 ‘forward’ propagation이라 한다.)
- Back propagation: output neuron에서 계산된 error를 각 edge들의 weight를 사용해 바로 이전 layer의 neuron들이 얼마나 error에 영향을 미쳤는지 계산한다. (output -> hidden 으로 정보가 흘러가므로 ‘back’ propagation이라 한다.)
Phase 2: Weight update
- Chain rule을 사용해 paramter들의 gradient를 계산한다.
이때, chain rule을 사용한다는 의미는 아래 그림에서 나타내는 것처럼, 앞에서 계산된 gradient를 사용해 지금 gradient 값을 update한다는 의미이다. (그림은 bengio의 deep learning book Ch6 에서 가져왔다.)
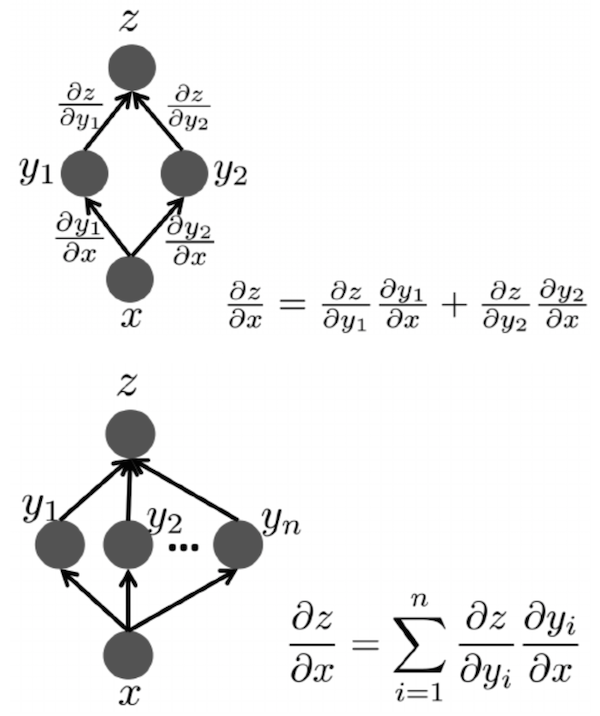
두 그림 모두 $\frac{\partial z}{\partial x}$를 구하는 것이 목적인데, 직접 그 값을 계산하는 대신, $y$ layer에서 이미 계산한 derivative인 $\frac{\partial z}{\partial y}$와 $y$ layer와 $x$에만 관계있는 $\frac{\partial y}{\partial x}$를 사용하여 원하는 값을 계산하고 있다. 만약 $x$ 아래에 $x^\prime$이라는 parameter가 또 있다면, $\frac{\partial z}{\partial x}$와 $\frac{\partial x}{\partial x^\prime}$을 사용하여 $\frac{\partial z}{\partial x^\prime}$을 계산할 수 있는 것이다. 때문에 우리가 backpropagation algorithm에서 필요한 것은 내가 지금 update하려는 paramter의 바로 전 variable의 derivative와, 지금 paramter로 바로 전 variable을 미분한 값 두 개 뿐이다. 이 과정을 output layer에서부터 하나하나 내려오면서 반복된다. 즉, output -> hidden k, hidden k -> hidden k-1, … hidden 2 -> hidden 1, hidden 1 -> input의 과정을 거치면서 계속 weight가 update되는 것이다. 예를 들어서 decision layer와 가장 가까운 weight는 직접 derivative를 계산하여 구할 수 있고, 그보다 더 아래에 있는 layer의 weight는 그 바로 전 layer의 weight와 해당 layer의 activation function의 미분 값을 곱하여 계산할 수 있다. 이해가 조금 어렵다면 아래의 예제를 천천히 읽어보기를 권한다.
이 과정을 맨 위에서 아래까지 반복하면 전체 gradient를 구할 수 있고, 이 gradient를 사용해 parameter들을 update할 수 있다. 이렇게 한 번의 iteration이 진행되고, 충분히 converge했다고 판단할 때 까지 이런 iteration을 계속 반복하는 것이 feed-forward network의 parameter를 update하는 방법이다.
이를 그림으로 표현하면 아래와 같다. (출처: 링크)
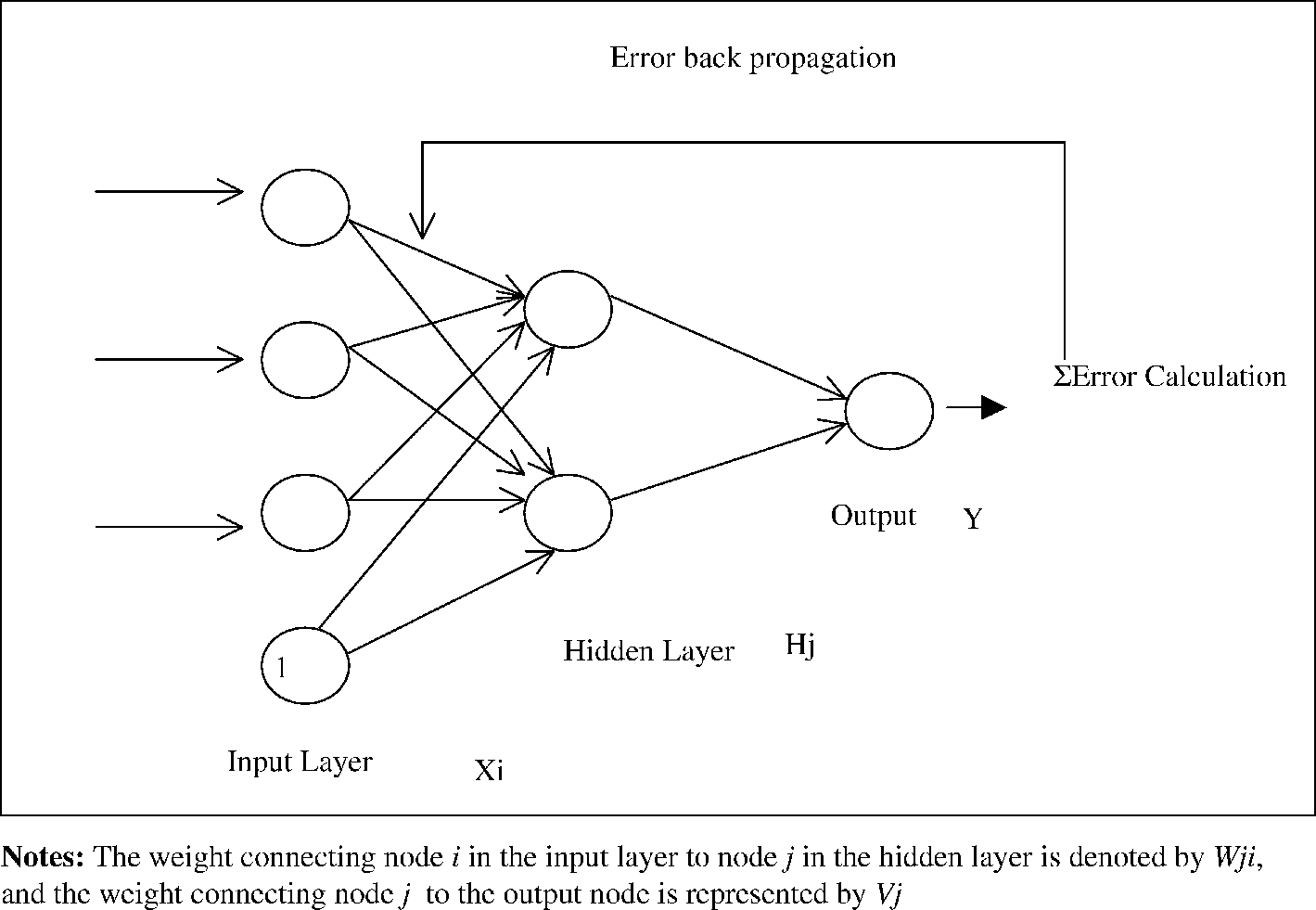
이렇듯 backpropagation은 직접 weight를 바로 변화시키는 것이 아니라 오직 error만을 보고 gradient descent method based approach를 사용해 error를 minimize하는 방향으로 계속 weight를 update시키는 것이다. 또한 한 번 error가 연산된 이후에는 output layer에서부터 그 이전 layer로 ‘역으로’ 정보가 update되기 때문에 이를 backpropagation, 한국어로는 역전사라고 하는 것이다.
Stochastic Gradient Descent
Gradient를 계산했으니 이제 직접 Gradient Descent를 써서 parameter만 update하면 된다. 그러나 문제가 하나 있는데, 일반적으로 neural network의 input data의 개수가 엄청나게 많다는 것이다. 때문에 정확한 gradient를 계산하기 위해서는 모든 training data에 대해 gradient를 전부 계산하고, 그 값을 평균 내어 정확한 gradient를 구한 다음 ‘한 번’ update해야한다. 그러나 이런 방법은 너무나도 비효율적이기 때문에 Stochastic Gradient Descent (SGD) 라는 방법을 사용해야한다.
SGD는 모든 데이터의 gradient를 평균내어 gradient update를 하는 대신 (이를 ‘full batch’라고 한다), 일부의 데이터로 ‘mini batch’를 형성하여 한 batch에 대한 gradient만을 계산하여 전체 parameter를 update한다. Convex optimization의 경우, 특정 조건이 충족되면 SGD와 GD가 같은 global optimum으로 수렴하는 것이 증명되어있지만, neural network는 convex가 아니기 때문에 batch를 설정하는 방법에 따라 수렴하는 조건이 바뀌게 된다. Batch size는 일반적으로 메모리가 감당할 수 있을 정도까지 최대한 크게 잡는 것 같다.
Backpropagation Algorithm: example
이전에 chain rule로 gradient를 계산한다고 언급했었는데, 실제 이 chain rule이 어떻게 적용되는지 아래의 간단한 예를 통해 살펴보도록하자. 이때 계산의 편의를 위해 각각의 neuron은 sigmoid loss를 가지고 있다고 가정하도록 하겠다.
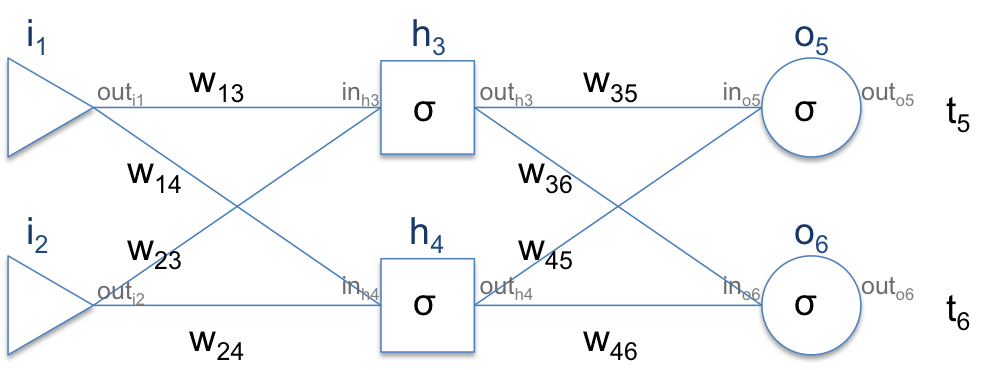
이때 각각의 neuron의 input으로 들어가는 값을 $in_{o_5}$, output으로 나가는 값을 $out_{h_3}$와 같은 식으로 정의해보자 (이렇게 된다면 in과 out은 $out_{h_3} = \sigma(in_{h_3})$ 으로 표현 가능하다. - 이때 $\sigma$는 sigmoid function). 먼저 error를 정의하자. error는 가장 간단한 sum of square loss를 취하도록 하겠다. 우리가 원하는 target을 $t$라고 정의하면 loss는 $E = \frac{1}{2}(t_5-out_{o_5})^2 + \frac{1}{2}(t_6-out_{o_6})^2$가 될 것이다 (1/2는 미분한 값을 깔끔하게 쓰기 위해 붙인 상관없는 값이므로 무시해도 좋다). 그리고 우리가 원하는 값들은 $\frac{\partial E}{\partial w_{13}}, \frac{\partial E}{\partial w_{14}}, \ldots, \frac{\partial E}{\partial w_{46}}$이 될 것이다. 이제 가장 먼저 $\frac{\partial E}{\partial w_{35}}$ 부터 계산해보자.
$$\frac{\partial E}{\partial w_{35}} = \frac{\partial E}{\partial out_{o_5}} * \frac{\partial out_{o_5}}{\partial in_{o_5}} * \frac{\partial in_{o_5}}{\partial w_{35}}. $$
즉, 우리가 원하는 derivative를 계산하기 위해서는 세 개의 다른 derivative ($\frac{\partial E}{\partial out_{o_5}}, \frac{\partial out_{o_5}}{\partial in_{o_5}}, \frac{\partial in_{o_5}}{\partial w_{35}}$)를 계산해야한다. 각각을 구하는 방법은 다음과 같다.
$\frac{\partial E}{\partial out_{o_5}}$: error를 $E = \frac{1}{2}(t_5-out_{o_5})^2 + \frac{1}{2}(t_6-out_{o_6})^2$라고 정의했으므로, $\frac{\partial E}{\partial out_{o_5}} = out_{o_5} - t_5$이다. - 이때 $out_{o_5}$와 $t_5$는 weight update이전 propagation step에서 계산된 값이다.
$\frac{\partial out_{o_5}}{\partial in_{o_5}}$: $o_5$는 sigmoid activation function을 사용하므로 $out_{o_5} = \sigma(in_{o_5})$이다. 또한 sigmoid function의 미분 값은 $\frac{\partial \sigma(x)}{\partial x} = \sigma(x) (1 - \sigma(x))$으로 주어지므로, 이 값을 대입하면 $\frac{\partial out_{o_5}}{\partial in_{o_5}} = out_{o_5} (1 - out_{o_5})$가 된다. - 역시 여기에서도 미리 계산한 $out_{o_5}$를 사용한다.
- $\frac{\partial in_{o_5}}{\partial w_{35}}$: $o_5$로 들어온 값의 총 합은 앞선 layer의 output과 $o_5$로 들어오는 weight를 곱하면 되므로 $in_{o_5} = w_{35} out_{h_3} + w_{45} out_{h_4}$이고, 이것을 통해 $\frac{\partial in_{o_5}}{\partial w_{35}} = out_{h_3}$가 됨을 알 수 있다. - $out_{h_3}$ 역시 이전 propagation에서 계산된 값이다.
따라서 $\frac{\partial E}{\partial w_{35}}$의 derivative 값은 위의 세 값을 모두 곱한 것으로 계산 할 수 있다. 그림으로 표현하면 아래와 같은 그림이 될 것이다. 즉, ‘backward’ 방향으로 derivative에 대한 정보를 ‘propagation’하면서 parameter의 derivative를 계산하는 것이다. 마찬가지 방법으로 $w_{36}, w_{45}, w_{46}$에 대한 derivative도 계산할 수 있다.
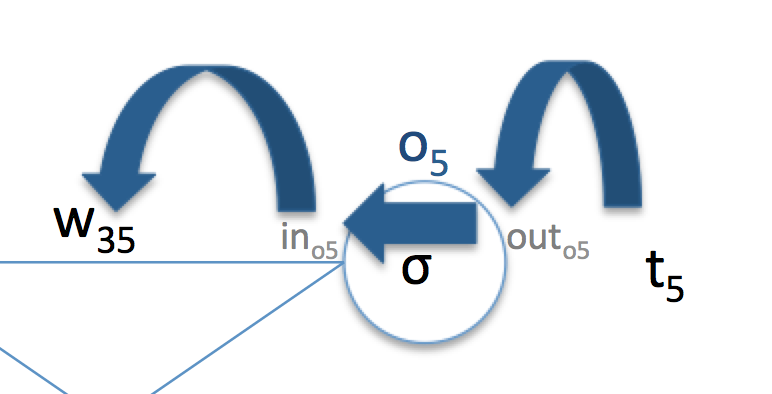
그럼 이번에는 그 전 layer의 paramter들 중 하나인 $w_{13}$의 derivative를 계산해보자. 이번에 계산할 과정도 위와 비슷한 그림으로 표현해보면 아래와 같다.
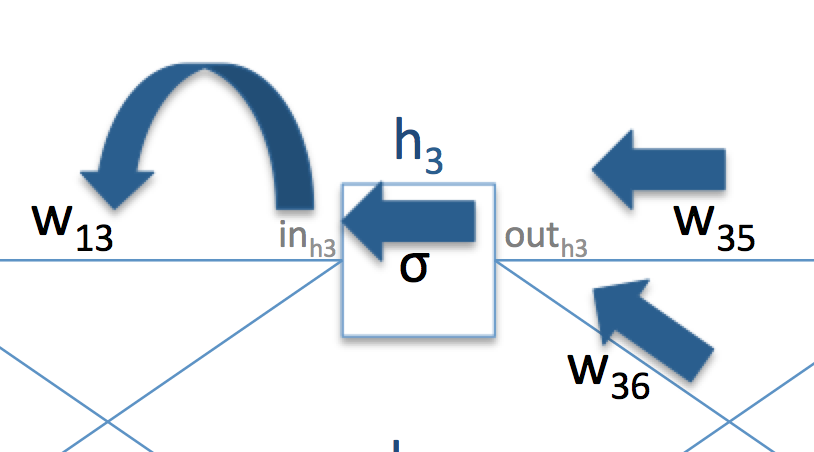
그러면 이제 $\frac{\partial E}{\partial w_{13}}$을 구해보자.
$$\frac{\partial E}{\partial w_{13}} = \frac{\partial E}{\partial out_{h_3}} * \frac{\partial out_{h_3}}{\partial in_{h_3}} * \frac{\partial in_{h_3}}{\partial w_{13}}.$$
마찬가지로 각각을 구하는 방법에 대해 적어보자.
$\frac{\partial E}{\partial out_{h_3}}$: $E = \frac{1}{2}(t_5-out_{o_5})^2 + \frac{1}{2}(t_6-out_{o_6})^2$를 $E = E_{o_5} + E_{o_6}$로 decompose 하면 이 미분 식은 $\frac{\partial E_{o_5}}{\partial out_{h_3}} + \frac{\partial E_{o_6}}{\partial out_{h_3}}$로 쓸 수 있다. 각각의 계산은 다음과 같다.
$\frac{\partial E_{o_5}}{\partial out_{h_3}} = \frac{\partial E_{o_5}}{\partial in_{o_5}} * \frac{\partial in_{o_5}}{\partial out_{h_3}}$으로 쓸 수 있다. 이 중 앞의 값인 $\frac{\partial E_{o_5}}{\partial in_{o_5}}$은 이미 전 과정에서 계산했던 $\frac{\partial E}{\partial out_{o_5}}$과 $\frac{\partial out_{o_5}}{\partial in_{o_5}}$의 곱으로 계산가능하다. 뒤의 값은 $\frac{\partial in_{o_5}}{\partial out_{h_3}} = w_{35}$이므로 간단하게 계산할 수 있다.
$\frac{\partial E_{o_6}}{\partial out_{h_3}}$도 위와 같은 방법으로 연산이 가능하다.
$\frac{\partial out_{h_3}}{\partial in_{h_3}}$: $\frac{\partial out_{o_5}}{\partial in_{o_5}}$와 같다. 따라서 $out_{h_3} (1-out_{h_3})$이다.
$\frac{\partial in_{h_3}}{\partial w_{13}}$: $\frac{\partial in_{o_5}}{\partial w_{35}}$와 같다. 따라서 $out_{i_1}$이다.
이렇게 $\frac{\partial E}{\partial out_{h_3}}$에서는 앞에서 계산했던 값들을 재활용하고, 아래의 값들은 activation function과 network의 topological property에 맞는 derivative를 곱하는 방식으로 $\frac{\partial E}{\partial w_{13}}$을 구할 수 있다.
이렇듯 backpropagation algorithm은 forward propagation을 통해 필요한 값들을 미리 저장해두고, backward propagation이 진행되면서 위에서부터 loss에 대한 derivative를 하나하나 계산해나가면서 다음 layer에서 바로 전 layer에서 계산한 값들과 각 neuron 별로 추가적으로 필요한 derivative들을 곱해나가면서 weight의 derivative를 계산하는 알고리즘이다.
이렇게 한 번 전체 gradient를 계산한 다음에는 learning rate를 곱하여 전체 parameter의 값을 update한 다음, 다시 처음부터 이 과정을 반복한다. 보통 에러가 감소하는 속도를 관측하면서 ‘이 정도면 converge한 것 같다’ 하는 수준까지 돌린다.
익숙해지려면 다소 시간이 걸리지만, 개념적으로 먼저 ‘error를 먼저 계산하고, 그 값을 아래로 전달해나가면서 바로 전 layer에서 계산한 미분값들을 사용해 현재 layer의 미분값을 계산한 다음, 그 값을 사용해 다음 layer의 미분값을 계산한다.’ 라고 개념만 이해해두고 다시 차근차근 chain rule을 계산해나가면서 계산하면 조금 편하게 익숙해 질 수 있을 것이다.
Backpropagation Algorithm: In Practice
실제 backpropagtion을 계산해야한다고 가정해보자. 편의상 $l$번째 hidden layer를 $y_l$ 이라고 해보자. 이 경우 각 layer에 대해 backpropagation algorithm을 위해 계산해야할 것은 총 두 가지 이다. Loss를 $E$라고 적었을 때 먼저 layer $l$의 parameter $\theta_l$의 gradient인 $\frac{\partial E}{\partial w_l }$을 구해야한다. 이 값은 $\frac{\partial E}{\partial w_l } = \frac{\partial E}{\partial y_{l} } \frac{\partial y_{l} }{\partial w_{l} } $을 통해 계산한다. 이때, $\frac{\partial E}{\partial y_{l} } = \frac{\partial E}{\partial y_{l+1} } \frac{\partial y_{l+1} }{\partial y_{l} } $이므로 $\frac{\partial E}{\partial y_{l} }$은 바로 전 layer에서 넘겨준 $\frac{\partial E}{\partial y_{l+1} }$의 값을 사용하여 계산하게 된다. 정리하면 실제 계산해야하는 값은 $\frac{\partial y_{l+1} }{\partial y_{l}},\frac{\partial y_{l} }{\partial w_{l} } $ 두 가지이고, 이 값들을 사용해 $\frac{E}{\partial y_{l}}, \frac{E}{\partial w_{l}}$을 return하게 된다. 앞의 값은 다음 layer에 넘겨줘서 다음 input으로 사용하고, 두 번째 값은 저장해두었다가 gradient descent update할 때 사용한다.
두 가지 예를 들어보자. 먼저 Inner Product layer 혹은 fully connected layer이다. 이 layer가 inner product layer라고 불리는 이유는 input $y_l$에 대해 output $y_{l+1}$이 간단한 inner product 들이 모여있는 형태로 표현되기 때문이다. 예를 들어 $y_{l+1, i}$를 l+1 번째 layer의 i 번째 node라고 한다면, $y_{l+1, i} = \sum_{j} w_{ij} y_{l, j}$으로 표현할 수 있음을 알 수 있다. 그런데 이 값은 사실 vector $w$와 $y_{l}$의 inner product로 표현됨을 알 수 있다. 그렇기 때문에 fully connected layer를 inner product라고 부른다. 다시 본론으로 돌아와서 inner product의 output은 input과 weight의 matrix-vector multiplication인 $y_{l+1} = W_l * y_l$으로 표현할 수 있다.
따라서 $\frac{\partial y_{l+1} }{\partial y_{l}} = W_l^\top$이고, $\frac{\partial y_{l} }{\partial W_{l} } = y_l$이다. 이 값을 통해 실제 return하는 값은 $\frac{\partial E }{\partial y_{l} } = \frac{\partial E }{\partial y_{l+1} } * W_l^\top $와 $\frac{\partial E }{\partial w_{l} } = \frac{\partial E }{\partial y_{l+1} } * y_{l} $이 된다.
두 번째로 많이 사용하는 ReLU non-linearity의 gradient를 계산해보자. 이때 activation function은 마치 하나의 layer가 더 있는 것처럼 생각할 수 있다. 즉 $y_{l+1} = max(0, y_{l})$로 표현할 수 있을 것이다. Parameter는 없으니까 생략하면 만약 $y_{l} \geq 0$라면 $\frac{\partial y_{l+1} }{\partial y_{l} = 1} $이고, 아니라면 0이 될 것이다. 따라서 $y_{l} \geq 0$라면 $\frac{\partial E }{\partial y_{l} } = \frac{\partial E }{\partial y_{l+1} } $이 되고, 0보다 작다면 0이 될 것이다.
정리
Deep learning을 다루기 위해서는 가장 먼저 aritifitial neural network의 model에 대한 이해와 gradient descent라는 update rule에 대한 이해가 필수적이다. 이 글에서는 가장 기초적이라고 생각하는 feed-forward network의 model을 먼저 설명하고, paramter를 update하는 gradient descent algorithm의 일종인 backpropagation에 대한 개념적인 설명을 다루었다. 조금 어려울 수 있는 내용이니 다른 글들을 계속 참고하면서 보면 좋을 것 같다.
Reference
- Deep Learning, Yoshua Bengio and Ian J. Goodfellow and Aaron Courville, Book in preparation for MIT Press, 2015
- wiki (링크)
- Caffe workshop - CNN backpropagation
변경 이력
- 2015년 9월 13일: 글 등록
- 2015년 9월 14일: 오타수정, SGD 내용 추가 등
- 2015년 9월 20일: BP in practice 추가
Machine Learning 스터디의 다른 글들
- Machine Learning이란?
- Probability Theory
- Overfitting
- Algorithm
- Decision Theory
- Information Theory
- Convex Optimzation
- Classification Introduction (Decision Tree, Naïve Bayes, KNN)
- Regression and Logistic Regression
- PAC Learning & Statistical Learning Theory
- Support Vector Machine
- Ensemble Learning (Random Forest, Ada Boost)
- Graphical Model
- Clustering (K-means, Gaussian Mixture Model)
- EM algorithm
- Hidden Markov Model
- Dimensionality Reduction (LDA, PCA)
- Recommendation System (Matrix Completion)
- Neural Network Introduction
- Deep Learning 1 - RBM, DNN, CNN
- Reinforcement Learning