README   SanghyukChun's Blog

Machine Learning 스터디 (8) Classification Introduction (Decision Tree, Naïve Bayes, KNN)

| Comments

들어가며

첫 번째 글에서 설명했던 것 처럼 Machine Learning은 크게 Supervised Learning, Unsupervised Learning 그리고 Reinforcement Learning으로 구분된다. 이 글에서는 그 중 Supervised Learning의 가장 대표적인 예시인 Classification에 대해 다룰 것이며 가장 대표적이고 간단한 세 가지 알고리즘에 대해서 역시 다룰 것이다.

What is Classification?

Classification은 Supervised Learning의 일종으로, 기존에 존재하는 데이터와 category와의 관계를 learning하여 새로 관측된 데이터의 category를 판별하는 문제이다. 스팸 필터를 예로 들어들어보자. 스팸 필터의 데이터는 이메일이고, category, 혹은 label, class는 spam메일인지 일반 메일인지를 판별하는 것이 될 것이다. 스팸필터는 먼저 스팸 메일, 그리고 일반 메일을 learning을 한 이후, 새로운 데이터 (혹은 메일)이 input으로 들어왔을 때 해당 메일이 스팸인지 일반 메일인지 판별하는 문제를 풀어야하며, 이런 문제를 classification이라고 한다.

첫 번째 글에서 머신러닝 문제는 먼저 주어진 데이터에 대한 가정을 하고, 해당 가정을 만족하는 best hypothesis를 찾는 문제라고 언급한 적이 있다. Classification 문제 역시 Machine Learning 문제이므로 데이터에 대한 가정을 먼저 해야하고, best hypothesis를 찾는 과정을 거친다. 따라서 각각의 서로 다른 classification algorithm들은 서로 다른 assumption을 가지고 있으며, 해당 assumption을 가장 잘 만족하는 function parameter를 계산하는 과정이다. 앞으로 설명하게 될 알고리즘들에 대한 설명을 읽을 때 데이터에 대해 어떤 가정을 하였는지 꼼꼼히 확인하면서 읽으면 알고리즘을 이해하기 한결 수월할 것이다.

Decision Tree

Decision Tree는 가장 단순한 classifier 중 하나이다. 이 Decision Tree의 구조는 매우 단순하다.

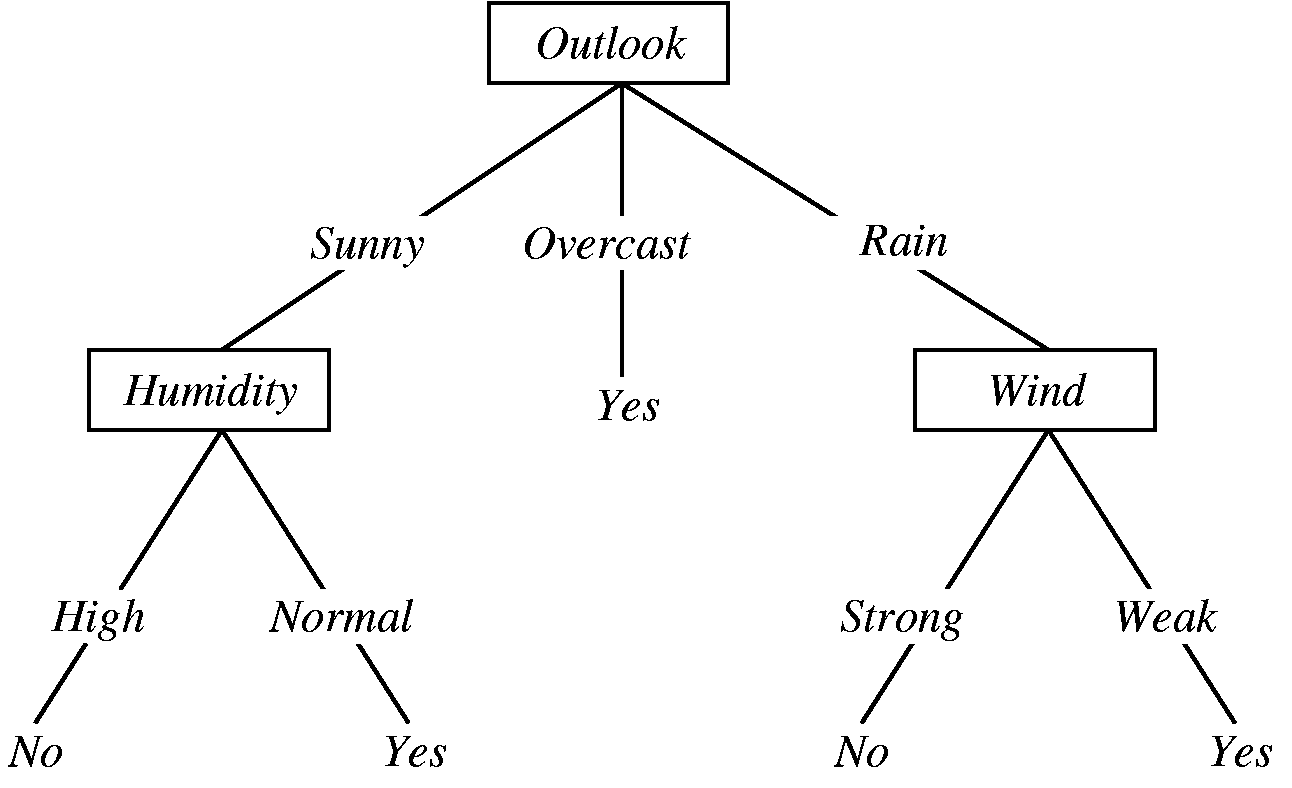
위의 그림은 오늘 외출을 할까 말까를 결정하는 decision tree이다. 이렇듯 decision tree는 tree구조를 가지고 있으며, root에서부터 적절한 node를 선택하면서 진행하다가 최종 결정을 내리게 되는 model이다. Decision tree의 가장 좋은 점은 단순하다는 점이다. 누구나 쉽게 이해할 수 있고, 그렇기 때문에 쉽게 디버깅할 수 있다. 예를 들어 위의 예시에서 습도가 높아도 나갈만하다는 생각이 든다면 맨 왼쪽의 No를 Yes로 바꾸기만 하면 간단하게 로직을 바꿀 수 있다. 그러나 다른 모델들은 그런 점들이 비교적 어렵다. Machine Learning에서 말하는 decision tree는 decision tree learning으로, 일일이 node마다 로직을 사람이 써넣어 만드는 것을 의미하는게 아니라, node 개수, depth, 각각의 node에서 내려야하는 결정 등을 데이터를 통해 learning하는 algorithm들을 사용해 만든 decision tree를 의미한다.

많이 쓰이는 알고리즘들로는 ID3, C4.5, CART, CHAID, MARS 등이 있으며, 보통 C4.5를 가장 많이 사용한다.

C4.5는 ID3의 몇 가지 문제점들을 개선한 알고리즘으로, 그 기본 개념은 ID3와 크게 다르지 않다. 추후 이 글 혹은 다른 글에 ID3 알고리즘에 대한 내용을 추가하도록 하겠다.

Regression Tree and Ensemble method

Decision tree는 output value가 반드시 binary여야한다는 제약조건이 있기 때문에 스팸 필터 등에서는 사용할 수 있지만, 실제 모든 데이터가 binary만을 output으로 가지지 않으므로 모든 데이터에 사용하려면 변형이 필요하다. Regression tree는 binary가 아니라 real value를 output으로 가지는 모델로, learning하는 방법은 크게 다르지 않다고 한다.

가끔은 하나의 decision tree를 사용하는 것이 아니라 한 번에 여러 개의 decision tree들을 만들어서 각각의 decision tree들이 내리는 결정을 종합적으로 판단하여 (ensemble) 결정을 내리기도 한다. Bagging decision tree, random forest등이 이에 속한다. 이런 식으로 여러 개의 classifier를 사용해 decision을 내리는 방법을 ensemble method라고 하는데, industry에서는 machine learning algorithm의 성능을 높이기 위해서 여러 개의 알고리즘들을 ensemble method를 사용하여 한 번에 같이 사용하기도 한다. 대표적인 예로 AdaBoost 등이 있다.

Ensemble method에 대해서는 나중에 따로 다시 설명할 예정이므로 그 글을 참고하면 좋을 것 같다. (링크는 추후 추가 예정)

Naïve Bayes

Naïve Bayes Classifier는 Bayesian rule에 근거한 classifier이다. Naïve Bayes는 일종의 확률 모델로, 약간의 가정을 통해 문제를 간단하게 푸는 방법을 제안한다. 만약 데이터의 feature가 3개 있고, 각각이 binary라고 해보자. 예를 들어 남자인지 여자인지, 성인인지 아닌지, 키가 큰지 작인지 등의 feature를 사용해 사람을 구분해야한다고 생각해보자. 이 경우 적어도 8개의 데이터는 있어야 모든 경우의 수를 설명할 수 있게 된다. 그런데 보통 데이터를 설명하는 feature의 개수는 이보다 훨씬 많은 경우가 많다. 예를 들어 feature가 10개 정도 있고 각각이 binary라면, 제대로 모든 데이터를 설명하기 위해서는 $2^{10}$, 약 1000개 이상의 데이터가 필요하다. 즉, 필요한 데이터의 개수가 feature 혹은 데이터의 dimension에 exponential하다. 이런 경우 그냥 Bayes rule을 사용해 분류를 하게 되면 overfitting이 되거나 데이터 자체가 부족해 제대로 된 classification을 하기 어려울 수 있다. Naïve bayes는 이런 문제를 해결하기 위해 새로운 가정을 하나 하게 된다. 바로 모든 feature들이 i.i.d.하다는 것이다. i.i.d는 independent and identically distributed의 준말로, 모든 feature들이 서로 independent하며, 같은 분포를 가진다는 의미이다. 당연히 실제로는 feature들이 서로 긴밀하게 관련되어있고 다른 분포를 가질 것이므로 이 가정은 틀린 가정이 될 수 있다. 그러나 만약 모든 feature가 i.i.d.하다고 가정하게 된다면 우리가 필요한 최소한의 데이터 개수는 feature의 개수에 exponential하게 필요한게 아니라 linear하게 필요하게 된다. 간단한 가정으로 모델의 complexity를 크게 줄일 수 있는 것이다. 때문에 Naïve Bayes 뿐 아니라 많은 모델에서 실제 데이터가 그런 분포를 보이지 않더라도 그 데이터의 분포를 특정한 형태로 가정하여 문제를 간단하게 만드는 기술을 사용한다.

조금 더 엄밀하게 수식을 사용해 설명을 해보자. 우리가 가지고 있는 input data 를 $x = (x_1, \ldots, x_n)$이라고 가정해보자. 즉 우리는 총 $n$개의 feature를 가지고 있다고 가정해보자 (보통 $n$은 데이터의 개수를 의미하지만, wikipedia의 notation을 따라가기 위하여 이 글에서도 dimension을 나타내기 위해 $n$을 사용하였다). 그리고 Class의 개수는 $k$라고 해보자. 우리의 목표는 $p(C|x_1, \ldots, x_n) = p(C|x)$를 구하는 것이다. 즉, 1부터 $k$까지의 class 중에서 가장 확률이 높은 class를 찾아내어 이를 사용해 classification을 하겠다는 것이다. Bayes rule을 알고 있으므로 이 식을 bayes rule을 사용해 전개하는 것은 간단하다.

$$ p(C|x) = \frac{p(C) p(x|C)}{p(x)} $$

이 때 분모에 있는 데이터의 확률은 normalize term이기 때문에 모든 값을 계산하고 나서 한 번에 계산하면 되므로 우리는 $p(x,C) = p(C) p(x|C)$, 다시 말해 prior와 likelihood를 계산해야만한다. 그러나 이 값은 joint probability이므로 데이터에서부터 이 값을 알아내기 위해서는 ‘엄청나게 많은’ 데이터가 필요하다. 구체적으로는 앞서 말한 것 처럼 dimension에 exponential하게 많은 데이터 개수를 필요로 한다. 그러나 만약 우리가 x가 모두 indepent하다고 가정한다면 간단하게 다음과 같은 식으로 나타낼 수 있다.

$$ p(C) p(x_1, \ldots, x_n | C) = p(C) p(x_1|C) p(x_2|C) \ldots = p(C) \prod p(x_i|C)$$

따라서 normalize term을 $Z$로 표현한다면, 우리가 구하고자 하는 최종 posterior는 $p(C|x) = \frac{1}{Z} p(C)\prod p(x_i|C)$로 나타낼 수 있게 된다.

KNN

K-Nearest Neighbors algorithm (KNN)은 구현하기 어렵지 않으면서도 비교적 나쁘지 않은 성능을 내는 Classification Algorithm 중 하나이다. KNN은 가까운 데이터는 같은 label일 가능성이 크다고 가정하고 새로운 데이터가 들어오면, 그 데이터와 가장 가까운 k개의 데이터를 training set에서 뽑는다. 뽑은 k개의 데이터들의 label을 관측하고 그 중 가장 많은 label을 새로운 데이터의 label로 assign하는 알고리즘이다 (이런 방식을 majority voting이라고 한다). 이때 ‘가까움’은 Euclidean distance로 측정해도 되고, 다른 metric이나 measure를 사용해도 된다. 이때 distance 혹은 similarity를 측정하기 위해서 반드시 metric을 사용해야하는 것은 아니다. 즉, metric의 세 가지 성질을 만족하지 않는 measure일지라도 두 데이터가 얼마나 ‘비슷하냐’를 measure할 수 있는 measure라면 KNN에 적용할 수 있다. 아래 그림은 KNN이 어떻게 동작하는지 알 수 있는 간단한 예시이다. 아래 그림을 보면 k를 3으로 골랐을 때 초록색 데이터의 label은 빨강이 되고, k를 5로 골랐을 때는 파란색이 됨을 알 수 있다.

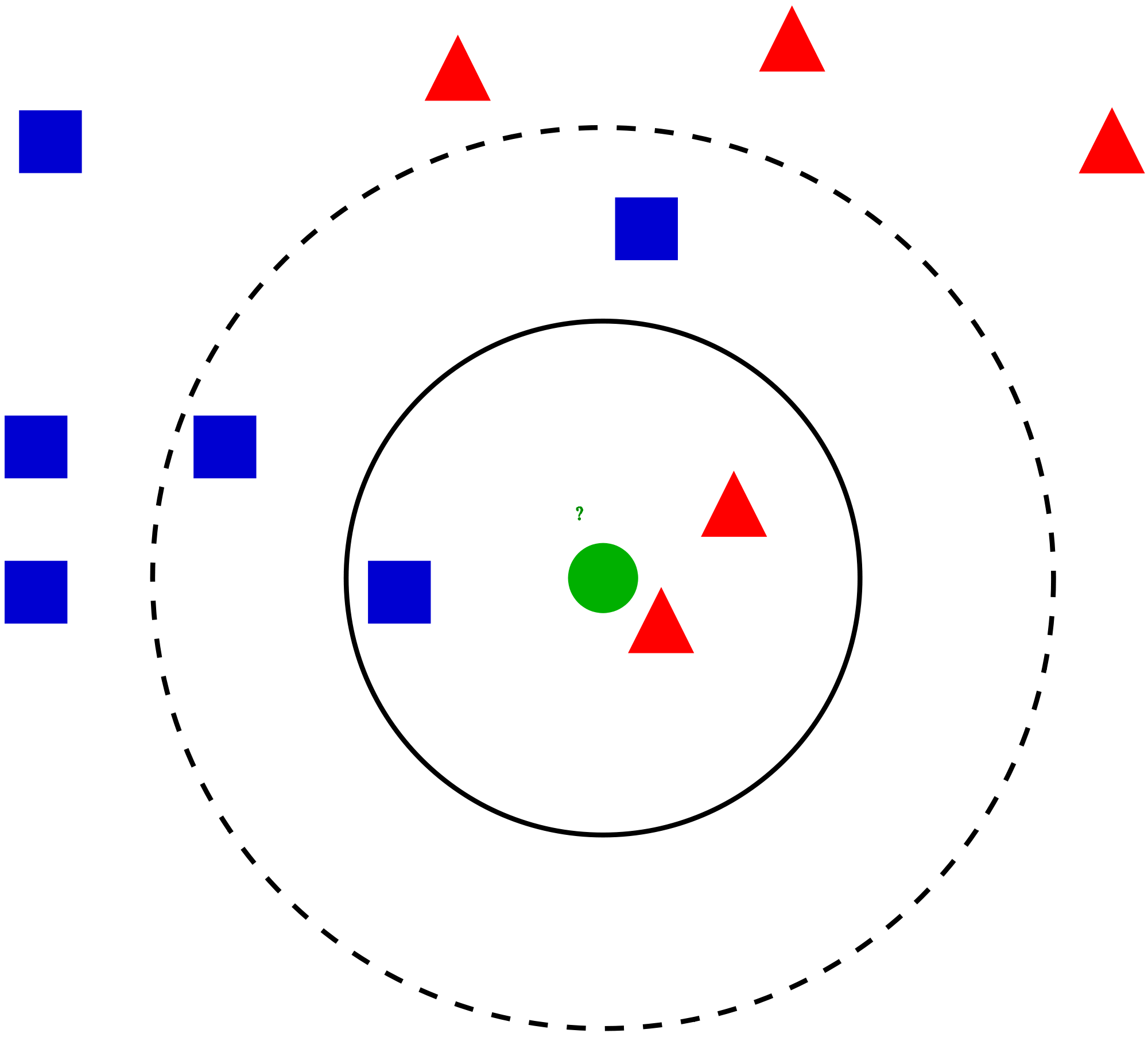
KNN은 구현하기에도 매우 간단하고 (새로 들어온 점과 나머지 점들간의 distance를 측정한 후 sorting하기만 하면 된다) 성능도 보통 크게 나쁘지 않은 값을 보이기 때문에 간단하게 개발할 필요가 있는 경우에 많이 사용하게 된다. 사실 대부분의 머신러닝 툴박스들은 KNN의 다양한 variation까지 built-in function으로 지원한다. Matlab의 knnclassify가 대표적인 예. 또한 KNN은 유용한 성질들이 많이 있다. 예를 들어 만약 데이터의 개수가 거의 무한하게 있다면, KNN classifier의 error는 bayes error rate의 두 배로 bound가 된다는 특성이 있다. 즉, 데이터가 엄청나게 많다면, KNN은 상당히 좋은 error bound를 가지게 된다는 것이다. 즉, 단순한 휴리스틱 알고리즘이 아니라 엄밀하게 수학적으로 우수한 알고리즘임을 증명할 수 있는 알고리즘이라는 뜻이다. 또한 distance를 마음대로 바꿀 수 있기 때문에 KNN은 변형하기에도 간단한 편이므로 데이터에 대한 가정을 모델에 반영하여 변형하기에 간편하다는 장점이 있다.

정리

가장 간단하게 적용할 수 있는 세 가지 classification algorithm에 대해 훑어보았다. 개인적으로 KNN은 정말 직관적일뿐 아니라 잘 동작하는 알고리즘이기 때문에, 개인적으로 어떤 문제를 해결해야할 때 가장 먼저 이 데이터가 어느 정도 잘 분류되는지 테스트하는 용도로 애용한다. 중요한 점은, 각각의 classification algorithm이 풀려고 하는 ‘문제’ 혹은 model은 서로 다른 가정을 가지고 있으며, 그 가정에 따라 문제를 푸는 방법이 아주 많이 바뀐다는 것이다. 즉, 어떤 새로운 classification algorithm을 만들어야 할 때는 (이는 classification 뿐 아니라 모든 알고리즘을 만들어야 할 때도 마찬가지인데) 먼저 어떤 문제를 풀어야하는지 문제를 정의해야하며, 문제를 정의하기 위해 어떤 모델을 가정해야한다는 것이다. 예를 들어 Naïve Bayes는 데이터의 각각의 feature들이 서로 i.i.d하다는 가정을 하고 있고, KNN은 ‘가까운’ 데이터와 내가 같은 label을 가지고 있을 확률이 높다는 가정을 하고 있다. 이렇듯 Machine learning algorithm을 개발하는 일에서 가장 중요한 것은 좋은 문제를 먼저 정의하는 것에서부터 시작하는 것이 아닐까 생각한다.

Reference

  • Bishop, Christopher M. Pattern recognition and machine learning. Vol. 4. No. 4. New York: springer, 2006. Chapter 9

변경 이력

  • 2015년 3월 25일: 글 등록

Machine Learning 스터디의 다른 글들