README   SanghyukChun's Blog

Machine Learning 스터디 (3) Overfitting

| Comments

들어가며

Overfitting은 Machine Learning Algorithm을 design하고 실제 구현을 할 때 Algorithm 설계를 제외하면 가장 어렵고 머리를 아프게 하는 문제 중 하나이다. Overfitting을 잘 관리하지 못하면 실전에서 써먹을 수 없는 알고리즘이 되기 때문에 overfitting을 잘 관리하는 것의 중요성은 몇 번을 강조해도 부족하지 않다. 보통 overfitting을 따로 chapter로 빼거나 하는 등으로 설명하는 경우가 많이 없지만, 나는 그만큼 overfitting과 관련된 이슈들이 중요하다고 생각하고, 다룰 얘기가 많다고 생각하기 때문에 이 글을 통해 overfitting의 개념과 그것을 해결하기 위한 방법, overfitting이 발생하는 근본적인 원인 등에 대해 다루도록 하겠다.

Overfitting

Overfitting이란 문자 그대로 너무 과도하게 데이터에 대해 모델을 learning을 한 경우를 의미한다. 현재에 대해 잘 설명하는 것 만으로 충분하지 않을까라고 생각할 수 있지만, 우리가 사실 원하는 정보는 기존에 알고 있는 데이터에 대한 것들이 아니라 새롭게 우리가 알게되는 데이터에 대한 것들을 알고 싶은 것인데, 정작 새로운 데이터에 대해서는 하나도 못맞추고, 즉 제대로 설명할 수 없는 경우라면 그 시스템은 그야말로 무용지물이라고 할 수 있을 것이다. 이전에 적은 포스트에서도 간략하게 다루고 있다.

Regularization

Overfitting을 어떻게 해결할까 고민하기에 앞서 먼저 Overfitting이 일어나는 이유는 무엇인가에 대해서 한 번 생각해보자. 먼저 overfitting의 가장 간단한 예시를 하나 생각해보자.

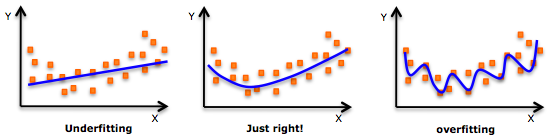
위 그림에서도 알 수 있 듯, 만약 우리가 주어진 데이터에 비해서 높은 complexity를 가지는 model을 learning하게 된다면 overfitting이 일어날 확률이 높다. 그렇다면 한 가지 가설을 세울 수 있는데, ‘complexity가 높을 수록 별로 좋은 모델이 아니다.’ 라는 가설이다. 이는 Occam’s razor, 오컴의 면도날이라 하여 문제의 solution은 간단하면 간단할수록 좋다라는 가설과 일맥상통하는 내용이다. 하지만 그렇다고해서 너무 complexity가 낮은 model을 사용한다면 역시 부정확한 결과를 얻게 될 것은 거의 자명해보인다. 그렇기 때문에 우리는 원래 cost function에 complexity와 관련된 penalty term을 추가하여, 어느 정도 ‘적당한’ complexity를 찾을 수 있다. 이를 regularization이라 한다. 이 이외에도 다양한 설명이 있을 수 있기에 위키 링크를 첨부한다.

그리고 이를 Bayesian 관점에서 설명을 할 수도 있다.

$$ p(Y|X) = {p(X|Y) p(Y) \over p(X)} $$

이전 글에서도 설명했던 것 처럼, 만약 우리가 어떤 사전지식, 혹은 prior knowledge가 존재한다면 단순히 observation만 하는 것 보다는 훨씬 더 잘 할 수 있을 것이다. 그리고 다시 Overfitting 문제로 돌아와서, overfitting이 생기는 가장 큰 이유는 너무 지금 데이터, 즉 observation에만 충실했던 것이 그 원인이다. 그러면 당연히 prior가 있으면 이를 해결할 수 있지 않을까? 라는 질문을 던질 수 있을 것이다. 즉, 우리의 prior는 high complexity solution은 나오지 않을 것이다. 어느정도 complexity가 높아지는 것 까지는 용인하지만, (표현할 수 있는 영역이 더 넓어지니까) 하지만 너무 그 complexity가 높아지면 문제가 생길 수 있다. 즉, 그런 high complexity를 가지는 solution이 나올 확률 자체가 매우 낮다. 라는 prior가 있다면 이를 간단하게 해결 할 수 있을 것이며, 이것이 결국 앞에서 봤었던 penalty와 동일하다는 것을 알 수 있다.

Model Selection

그런데 제 아무리 우리가 좋은 prior를 넣고, 좋은 penalty term을 design하더라도 만약 우리가 제대로 되지 않은 데이터들을 이용해 learning을 한다면 문제가 생길 수 있다. 마치 장님 코끼리 만지듯 전체 데이터는 엄청나게 많이 분포해있는데 우리가 가진 데이터가 아주 일부분에 대한 정보라면, 혹은 갑자기 그 상황에서 갑자기 노이즈가 팍 튀어서 데이터가 통채로 잘못 들어온다면? 아마 그런 데이터로 learning을 했다가는 sample bias가 일어나게 되어 크게 성능이 저하되게 될 것이다. 사실 위에 complexity라는 말도 결국에는 ‘Data point 대비 높은 complexity’가 더 정확한 말이다. 이를 최대한 피하기 위하여 우리는 generalization 이라는걸 하게 되는데, 다시 말해서 우리의 solution이 specific한 결과만을 주는 것이 아니라 general한 결과를 주도록 하려는 것이다. 이를 위한 여러 방법이 있을 수 있지만, 가장 많이 사용하는 방법은 validation set이라는 것을 사용하는 것이다. 즉, 모든 data를 전부 training에 사용하는 것이 아니라, 일부만 training에 사용하고 나머지를 일종의 validation을 하는 용도로 확인하는 것이다. 만약 우리의 모델이 꽤 괜찮은 모델이고, validation set이 잘 선택이 되었다면 training set에서만큼 validation set에서도 좋은 결과가 나올 수 있을 것이다.

보통 전체 데이터 중에서 training과 validation의 비율은 8:2로 하는 것이 일반적이다. 하지만 만약 validation set이 너무 작다면, 이 마저도 좋은 결과를 내기에는 부족할 수 있다. 이를 해결할 수 있는 컨셉 중에서 cross-validation이라는 컨셉이 있는데, validation set을 하나만 가지는 것이 아니라 여러개의 validation set을 정해놓고 각각의 set에 대해서 learning을 하는 것이다. 예를 들어 우리가 데이터가 X={1,2,3,4,5,6,7,8,9,10} 이 있을 때, 첫 번째 learning에서는 {1,..,8}을 사용해 learning하고 그 다음에는 {2,..,9}까지 learning하는 식으로 모든 permutation에 대해서 learning을 할 수 있을 것이다. 그리고 당연히 이런 방식으로 여러번 learning을 하게되면 그 때 얻어지는 model parameter는 그때그때 달라질텐데, cross-validation은 그 값들을 적당히 사용하여 가장 적절한 parameter를 얻어내는 방식이다. average로 해도 되고, median으로 해도 되고, 여러 방법이 있을 수 있다. cross-validation의 단점은 algorithm의 running time이 데이터의 크기 뿐 아니라 validation을 하기 위한 그 여러 set들에 dependent하다는 것이다. 그리고 데이터가 많아지면 그런 validation set이 엄청나게 많아진다. 정확히는 exponential로 늘어나기 때문에 마냥 모든 데이터에 대해 cross-validation을 하는 것은 불가능하다.

그렇기 때문에 실제로 cross-validation을 할때는 모든 데이터를 사용하지는 않고, 적당히 몇 개의 set을 골라서 여러 번 model parameter를 ‘적당히’ 구하는 방법을 사용한다. 물론 이론적으로 AIC, BIC 등의 개념이 존재하여 이에 맞춰서 모델을 고르는 방법도 존재하지만 (AIC는 Akaike Information Criterion이고 BIC는 Bayesian Information Criterion으로, 둘 다 어떤 ‘information criteria’를 사용하느냐에 대한 내용이다.) 지금 내가 다루고자 하는 내용에서 좀 벗어나기 때문에 나중에 여유가 되면 이에 대한 글을 작성해보도록하겠다.

Curse of dimension

그러나 이게 끝이 아니다. 우리가 싸워 이겨내야할 문제들은 complexity, number of data 뿐 아니라 dimension of data 역시 존재한다. 즉, 우리가 1차원의 데이터를 다루는 것과 10000차원의 데이터를 다루는 것과는 정말 어마어마한 차이가 존재한다는 것이다. 이렇게 차원이 높은 데이터를 다룰 일이 있을까? 하고 약간 막연하게 생각할 수 있지만, 가장 간단한 예로, 100px by 100px 그림은 각각의 픽셀이 하나의 차원이라고 했을 때 10000차원 벡터로 표현이 가능하다. 실제로 머신러닝 분야에서 이미지를 다룰 때는 이런 식으로 처리를 하게 된다. 이 이외에도 high dimensioanl space 상에 존재하는 데이터를 다룰 일은 매우 많이 존재한다.

그렇다면 이런 high dimensional data가 왜 우리가 learning한 system의 성능을 나쁘게 만들까? 정말 간단하게 생각해보자. 만약 우리가 주어진 공간을 regular cell로 나눴다고 가정해보자. 그리고 각각의 cell에 가장 많이 존재하는 class를 그 cell의 class로 생각하여 무조건 그 cell에 존재하는 데이터는 그 class라고 하는 logic을 생각해보자. 당연히 cell의 개수를 무한하게 가져가게 된다면, 그리고 데이터가 무한하다면 이 logic은 반드시 truth로 수렴하게 될 것이다. 이 알고리듬이 제대로 동작하려면 각각의 cell, 혹은 bin이 반드시 차있어야한다. 즉, 비어있는 empty cell이 존재해서는 안된다. 따라서 데이터는 아무리 적어도 cell의 개수만큼은 존재해야한다. 그런데 이렇게 cell을 만들게 될 경우 그 cell의 개수는 dimension이 증가함에 따라 exponential하게 늘어나게 되는 것이다. 예를 들어 우리가 1차원상에서 3개의 bin을 가지고 있다고 하면, 이는 2차원상에서는 9개, 3차원상에서는 27개.. 이렇게 exponentially grow하게 되는 것을 알 수 있다. 이 모델의 parameter들이 exponentially 증가하는 것이다. (아래 슬라이드(출처) 참고)

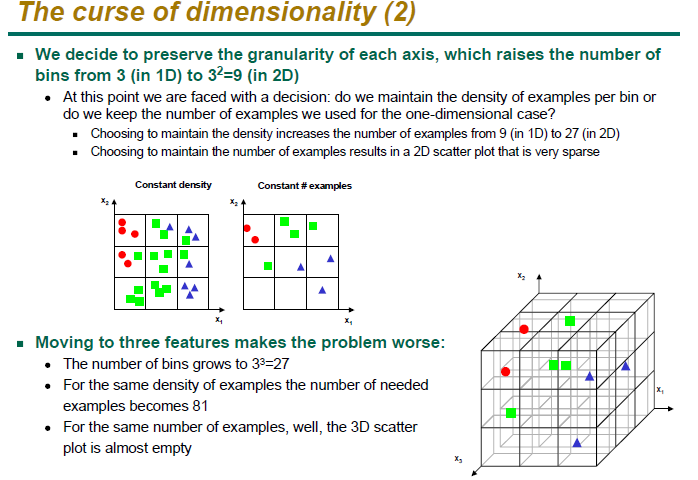
따라서 당연히 각각의 bin이 비어있지 않도록 ensure해줄 수 있는 data의 개수 역시 exponentially 하게 늘어나게 되고, 즉 차원이 증가하게 되면 필요한 데이터가 exponentailly하게 늘어나게 된다는 것을 의미한다. 그러나 당연히 우리가 3차원 데이터보다 100000차원 데이터를 exponential하게 더 많이 가지고 있으리라는 법은 없고, 이로 인해 문제가 발생하게 되는 것이다.

그리고 또 문제가 되는 것은 high dimensional space에서 정의되는 metric들로, 특히 2-norm 혹은 euclidean distance의 경우는 그 왜곡이 매우 심하여, 실제 멀리 떨어진 데이터보다 별로 멀리 떨어져있지 않고 각 dimension의 방향으로 약간의 noise가 섞여있는 데이터에 더 큰 distance를 부여하는 등의 문제가 존재한다.

조금 다른 예를 들어보자. 만약 D-dimensional space에서 엄청나게 얇은 구각을 만들었다고 생각해보자. 여기에서 ‘구’ 라는 것은 한 점에 대해 거리가 동일하게 떨어져있는 모든 점 내부의 영역을 의미한다는 것은 당연한 것이고.. 이 구의 부피는 $V_D(r)=K_D r^D$ 가 될 것이며, $K_D$는 그냥 D에 대한 상수라고 생각하면 된다. 그럼 반지름이 1이고 두께가 $\epsilon$인 구각의 부피와 반지름이 1인 구의 부피의 비율은 ${V_D(1) - V_D(1-\epsilon) \over V_D(1)} = 1-(1-\epsilon)^D$ 가 될 것이다. 놀랍게도, 만약 very very high dimension D에서는 이 값이 1로 수렴하게 된다. 즉, 매우 얇은 구각의 부피가 구의 부피와 같다는 의미. 혹은 대부분의 부피가 거의 surface에 가까운 엄청나게 얇은 그 shell에 존재한다는 희한하고 요상한 의미가 된다.

즉, high dimension은 (1) model의 complexity도 증가시키며 (2) 필요한 데이터의 양도 exponentially 하게 늘어나게 하고 (3) 우리가 기존에 사용하던 metric이 제대로 동작하지 않는 그야말로 끔찍한 환경이라 할 수 있다. 그래서 이런 high dimensional space에서 일어나는 여러 문제점들을 통틀어 Curse of dimension이라 한다.

이를 해결하기 위해서는 결국 feature extraction 등의 기술을 사용하여 dimension을 가장 적절하게 낮추는 것이 바람직하다고 할 수 있다.

Bias-variance Trade-off

Bias-variance trade-off 라는 개념은 사실 굉장히 유명한 개념이다. 간단하게 말하면 bias와 variance는 어쩔 수 없는 trade-off 관계를 가지고 있다는 의미이다. 자세한 증명과정은 링크해둔 위키피디아를 참고하면 된다. 간단히 컨셉만 언급하자면, Bias는 평균적으로 우리의 가설 h(x)가 얼마나 실제 현상 y(x)와 떨어져 있느냐에 대한 얘기이다. 즉, bias가 낮을수록 실제 현상에 유사하며, bias가 높을수록 실제 현상과 멀어진다. 이는 실제로 bias라는 단어가 가지고 있는 의미와 거의 유사하다. Variance는 평균에서 얼마나 멀리 떨어져있느냐를 의미하는데, variance가 높을수록 데이터들이 평균과 멀리 떨어져있고, variance가 낮을수록 데이터들은 평균과 가깝게 분포하여있다. 재미있는 점은 이 둘이 완전한 trade-off관계를 가지고 있다는 것인데, 증명 아이디어는, h(x)와 y(x)의 expected squared error를 계산해봤을 때 그 값이 정확하게 bias와 variance들에 대한 표현으로 decompose가 된다는 것이다. 주어진 데이터에 대해 bias가 낮으면 variance가 높고, bias가 높으면 variance가 낮다. 그런데 이때 bias는 overfitting 혹은 generalize에 대한 term이 되는데, 이유는 현재 관측하고 있는 데이터에 대해 bias가 낮다는 의미는 지금 데이터에만 너무 치중이 되어있다는 의미가 되기 때문이다. 즉, 너무 낮은 bias는 곧 overfitting과 거의 같은 의미라고 할 수 있다. 그 뿐 아니라 높은 variance는 다시 말해 complexity가 높다는 의미로도 받아들일 수 있기 때문에, 너무 낮은 bias 혹은 높은 variance를 피해야한다. 그렇지만 bias가 높은게 능사는 아닌데, 자칫 잘못하면 너무 bias가 높은 underfitted된 모델을 얻을 수도 있기 떄문이다. 즉, bias는 지금 내가 보고 있는 데이터를 얼마나 신뢰하느냐에 대한 척도라고 할 수 있는데, 지금 내가 보고 있는 데이터를 아예 신뢰하지 않는다고 한다면, 이는 machine learning을 통해 model을 얻었을 때 그 모델이 잘 동작할 것이라고 기대하기는 힘들 것이다.

굉장히 좋은 글을 발견해서 링크를 추가하도록 하겠다. 혹시 더 관심이 있는 사람들은 이 글을 읽어보면 될 것 같다.

Overfitting and Robustness

마지막으로 Robustness라는 개념에 다루고 글을 마치도록 하겠다. 지금까지 overfitting에 대한 설명을 읽어보면 알 수 있듯, overfitting이라는 것은 generalize라는 concept과 거의 정반대의 개념이라는 것을 알 수 있다. Generalize라는 개념은 일부분에만 잘 설명이 되는 것이 아닌 일반적으로도 잘 맞아 떨어지는 설명을 할 수 있도록 시스템을 만드는 것이라 생각하면 편한데, 다시 말해서 overfitting이 적은 시스템을 만드는 것이라고 생각할 수 있다. 이 generalize라는 개념을 생각할 때에 robust라는 개념도 같이 생각을 할 필요가 있는데, 매우 간단하게 설명하면, robust라는 컨셉은 ‘잘못된 데이터가 들어와도 시스템이 크게 변하지 않는 것’ 이라고 할 수 있다. 이때 잘못된 데이터를 흔히 outlier라고 하는데, 전혀 엉뚱한 데이터가 시스템에 들어온 경우 이 데이터로 인해 전체 시스템의 성능이 저하되지 않도록 하는 것을 의미한다. 보통 이런 엉뚱한 데이터는 noise에 의해 발생하게 되므로, robust라는 개념은 noisy한 환경에 덜 취약한 시스템을 구축하는 것이라 이해해도 좋을 것이다. 보통 robust한 시스템을 만들 때에 많이 사용하는 것은 metric을 변경하는 것이다. 즉, 대부분의 machine learning algorithm들이 metric을 기반으로 한 것들이 많은데, 거의 대부분이 2-norm의 제곱인 Euclidean distance를 사용한다. 때문에 이는 데이터의 제곱에 루트를 씌운 것에 또 제곱을 취하기 떄문에 그냥 절대값을 더하는 l1 norm등에 비해 outlier에 더 취약하다. 가장 robust한 norm은 l0 norm이지만 이것은 non-convex하기 때문에 보통 l1 norm으로 relax시켜서 계산을 하게 된다. 이런 robust system에 대해서는 이번 스터디에서는 직접 다루지는 않을 예정이지만, 현재 내 연구가 이쪽인만큼, 언젠가 한 번 큰 주제로 다뤄볼 수 있도록 하겠다.

변경 이력

  • 2014년 8월 4일: 글 등록
  • 2014년 10월 9일: 구성 변경 및 내용 추가 (Bayes, Model Selection 등)
  • 2015년 2월 28일: 변경 이력 추가, 문장 표현 등 수정

Machine Learning 스터디의 다른 글들