README   SanghyukChun's Blog

Machine Learning 스터디 (20-1) Multi-armed Bandit

| Comments

들어가며

이 글에서는 reinforcement learning의 한 갈래 중 하나인 Multi-armed Bandit에 대해 다룰 것이다. Multi-armed Bandit이 어떤 문제인지에 대해 간략히 설명한 다음, 좀 더 formal하게 문제를 정의하고, 이 문제를 푸는 여러 알고리즘들에 대해 다룰 것이다. 연구가 워낙 오래 진행된 분야라서 모델이나 알고리즘의 종류가 엄청나게 많지만, variation 중에서 몇 가지 간단한 것들 위주로 설명해보도록 하겠다.

Motivation: Exploration and Exploitation Trade-off

외팔이 강도가 (one-armed bandit이) 우연한 기회로 눈 앞에 여러 개의 슬롯머신을 공짜로 H시간 동안 플레이 할 수 있는 기회를 얻었다고 생각해보자. 이때 강도는 한 번에 한 개의 슬롯머신의 arm만 당길 수 있으며 (즉 총 H번 시도할 수 있다) 각각의 슬롯머신에서 얻을 수 있는 reward는 다르다고 가정한다. 또한 reward는 어떤 probabilistic distribution에 의해 draw되는 random variable이라고 했을 때, 이때 강도가 가장 수익을 최대화하기 위해서는 arm을 어떤 순서대로, 어떤 policy대로 당겨야할까?

그림 출처: MS research

이 문제에서 가장 큰 난점은, 슬롯머신마다 보상이 다르고, 한 번에 한 슬롯머신의 reward만 관측할 수 있다는 점이다. 예를 들어 한 슬롯머신을 골라서 계속 그 슬롯머신만 당길 수도 있겠지만, 이 경우 다른 슬롯머신에서 더 좋은 reward를 얻었을 수도 있기 때문에 가장 최적의 전략은 아닐 것이다. 혹은 모든 슬롯머신을 동일한 횟수만큼 반복할 수도 있을 것이다. 그러나 슬롯머신 중에서 가장 좋은 reward를 보이는 머신은 오직 하나 뿐 일 것이므로, 이런 전략은 마찬가지로 최종 reward를 최적화하는 방법은 아닐 것이다. 혹은 일부 시간만 슬롯머신을 랜덤하게 당겨보고, 그 시간 동안 제일 좋았던 슬롯머신만 계속 당겨보는 수도 있을 것이다. 이때 기존 경험 혹은 관측값을 토대로 가장 좋은 arm을 선택하는 것을 exploitation이라 하며 더 많은 정보를 위하여 새로운 arm을 선택하는 것을 exploration이라고 한다. 결국 시간이 제한되어있기 때문에 이 둘 사이에는 trade-off관계가 성립하게 된다. 만약 exploration를 너무 하지 않게 될 경우, 잘못된 정보를 토대로 exploitation을 하게 되기 때문에 최종 결과가 좋을 거라는 보장을 하기가 힘들 것이다. 그렇다고 해서 너무 exploration을 많이 하게 되면, 충분히 정보를 가지고 있음에도 불구하고 더 정보를 얻기 위해 쓸데 없는 비용이 발생할 것이다. 따라서 이런 측면에서 exploration과 exploitation은 서로 trade-off 관계가 있다고 할 수 있고, 이런 상황에서 우리가 이 둘을 어떻게 조절하느냐가 Multi-armed Bandit problem의 핵심이 되는 것이다.

이런 유형의 문제의 가장 대표적인 예시는 여러 개의 새로운 치료법 중에서 실제로 환자들에게 trial을 해보고 가장 좋은 치료법을 찾는 clinical trial이라고 불리는 문제이다. 예를 들어 우리가 에이즈에 효과가 있어보이는 약물이 총 K개가 있다고 했을 때, 환자들에게 서로 다른 약물을 (혹은 치료법을) 시도해보면서 가장 효과가 좋은 약물이 어떤 것인지 찾아내는 문제이다. 이 경우 당연히 환자들의 건강상 문제라거나 고통 등의 문제를 최소화하는 방향으로 치료 순서를 정해야할 것이다. 이 문제를 푸는 가장 단순한 방법은 K개의 약물을 각각 n번 시도 해보고 각각의 expectation을 고르는 방법이 있다. 그러나 K와 n에 따라 너무 많은 시간이 필요할 뿐 아니라, 이 중에서 환자에게 치명적인 약물이 있으면 risk minimization이라는 측면에서 문제가 된다. 이런 문제점을 해결하기 위해 Multi-armed bandit을 사용하게 되며, Mutli-armed bandit을 사용하게 되면 이런 형태의 문제들을 굉장히 효율적으로, 그리고 practical하게 잘 동작하는 방식으로 풀 수 있다.

또 다른 예시로는 웹 사이트의 A/B 테스트를 들 수 있다. 만약 K개의 시안 중에서 가장 사람들이 좋아할만한 시안이 무엇인지 알고 싶어서 사람들에게 무작위로 K개의 시안을 보여준다고 생각해보자. 역시 한 사람에 한 번에 한 페이지만 보여줄 수 있기 때문에 이 문제도 위의 문제와 비슷하게 다룰 수 있고, 가장 최적화하고 싶은 값은 click rate라거나 광고 수익률 등이 될 것이다. 실제로 구글 analytics에서도 multi-armed bandit 실험을 제공하고 있다 ([2]). 그 밖에 네트워크 상에서 delay를 최소화하는 route를 구하고 싶을 때, MAB를 활용해 adaptive routing을 하거나, 여러 개의 schedule queue가 있을 때 MAB를 사용해 task를 효과적으로 scheduling하는 방법도 존재하는 등, 수 많은 application들이 존재한다.

Multi-armed Bandit Problem

그러면 이제 Multi-armed Bandit 문제를 좀 더 엄밀하게 정의해보자. Multi-armed bandit (혹은 단순히 bandit이나 MAB) 문제는 각기 다른 reward를 가지고 있는 여러 개의 슬롯머신에서 (Multi-armed) 한 번에 한 슬롯머신에서만 돈을 빼갈 수 있는 도둑(one-armed bandit)의 H 시간 후의 최종 보상을 maximize하는 문제이다. Bandit 문제에서 player는 매 시간 t마다 K개의 arm 중에 하나를 선택, 혹은 play할 수 있고, 그에 상응하는 reward distribution에서 draw된 보상 x를 받게 된다. Bandit에서 매 시간마다 arm을 고르는 방법을 strategy 혹은 policy라고 부르며, bandit 문제는 시간 H 후의 최종 reward를 maximize하는 (혹은 regret을 minimize하는) policy를 찾는 문제가 된다.

Bandit problem이 기존 general reinforcement learning과 가장 크게 다른 점이라면, reinforcement learning은 매 순간 reward를 전부 정확하게 알고 나서 행동하지만, bandit problem에서는 오직 내가 지금 선택한 arm에 대한 보상(payoff)만 알 수 있고, 나머지 arm들의 payoff에 대해서는 알 수 없다는 점이다. 이런 ‘partial information’ 특성이 bandit problem의 가장 독특한 특징으로, 다른 arm들이 t 시간에 얼마만큼의 payoff를 주는지 알 수 없기 때문에 문제가 조금 더 까다로워지는 것이다.

Bandit problem에는 정말 많은 variants가 존재한다. 이 글에서는 가장 기본적인 (finite-aremd) stochastic bandit problem에 대해서만 다룰 것이다. Stochastic bandit problem에서 ‘stochastic’이라는 의미는 각각의 arm이 stochastic하게 특정 reward distribution에 의해 (모든 arm과 과거 play들에 대해 i.i.d.하게) draw된다고 가정한다. 또한 arm의 개수 K와 arm에서 나오는 payoff function x는 finite하고, stationary하다고 (즉, time-invariant하다고) 가정하게 된다. 마지막으로 우리가 arm을 play할 수 있는 시간 H 역시 finite하고 알려져 있다고 가정한다. 이런 문제를 finite-armed, stochastic multi-armed bandit problem이라 부른다. 참고로 보통 이론적인 분석을 할 때에는 각 arm의 reward distribution은 Bernoulli distribution을 많이 고른다. 따라서 많은 문제 세팅에서 각 시간마다 arm의 reward는 0 또는 1로 설정하게 된다.

실제로는 위의 조건이 상당히 strong하기 때문에, 여러 조건들이 relax될 수가 있다. 예를 들어 i.i.d. condition이라거나, finite, stationary arm condition이라거나 등의 조건들이 relax되는 variant도 존재한다. 우리가 아래에서 다룰 문제는 finite-armed, stochastic multi-armed bandit이 될 것이며, 당장은 contextual bandit이나 adversarial bandit 등의 variant들은 고려하지 않도록 하겠다. 실제로 bandit 문제는 앞서 정의한 statistical한 assumption에 의해서도 variant가 생길 수 있고, stochastic한 성질을 사용하고 하지 않느냐에 따라 또 달라지고, arm의 개수나 한 번에 관측할 수 있는 arm이 여러 개 있다거나, regret function을 어떻게 정의하느냐에 따라 엄청나게 많은 variant가 존재한다.

이제 bandit problem들의 variant에 대해서는 그만 이야기해보고 마지막으로 regret function에 대해 살펴보자. Regret이란, 개념적으로는 가장 optimal한 policy대로 arm을 play했을 때 얻어지는 reward에서 내 policy대로 play했을 때 얻어지는 reward의 차이이다. 개념적으로는 이렇지만, 실제로는 Regret function을 정의하는 방법에는 엄청나게 많은 종류가 있다. 물론 이 글에서는 그 모든 variant를 다루지 않고 대신 다음과 같이 생긴 가장 간단한 regret을 사용하도록 하겠다. 이때, $S_t$는 내 strategy로 time t 때 고른 arm의 index이다.

$$R = \left(\max_{i=1,\ldots,K} \mathbb E \sum_{t=1}^H x_{i,t}\right) - \mathbb E \sum_{t=1}^H x_{S_t,t}$$

혹은 다음과 같이 time t에서의 optimal policy로 얻은 reward $\mu_t^*$와 time t에서의 user의 policy로 얻은 reward $\mu_t$ 표현하기도 한다.

$$R = \mathbb E \left[ \sum_{t=1}^H\left(\mu_t^* - \mu_t\right) \right]$$

다시 말해서 reward function은 처음부터 끝까지 가장 optimal한 policy를 취했을 때의 reward expectation에서 내 policy를 취했을 때의 reward expectation을 뺀 값이다. 앞에서 언급한 것처럼 reward는 (보통 Bernoulli distribution에서 draw되는) random variable이기 때문에 조금 더 정확한 분석을 위해서 expectation을 취하게 되는 것이다. 그러나 이 값은 모든 reward를 알고있는 절대자 (oracle)이 있어야 정확한 값을 구할 수 있기 때문에 실제로 많은 실제 문제에서 regret이 얼마나 되는지 계산할 수는 없다. 대신 이론적인 분석을 할 때에, 미리 각 arm들이 특정 distribution을 따른다고 가정하고 특정 distribution을 가지는 arm들에서 bandit algorithm이 얼마나 regret을 minimize할 수 있는지를 분석하는 데에 쓰인다고 생각하면 된다.

더 많은 bandit variant들이나 regret function의 종류에 대해 궁금하다면 reference로 참조한 survey paper [1]를 읽어보길 권한다.

Algorithm 0: Gittins index

앞서 설명한 bandit problem을 풀기 위한 알고리즘으로 가장 먼저 설명할 알고리즘은 Gittins index이다. 이 알고리즘은 이론적으로 잘 증명되어있는 Bayes-optimal policy이지만, 실제로는 computation이 너무 많이 필요하기 때문에 practical하게 사용되는 대신 다른 알고리즘들이 많이 사용된다. 따라서 이 문단에서는 정말 짤막하게 언급만 하고 넘어가려고 한다. 매 time t마다 Gittins index 알고리즘은 다음과 같은 방식으로 arm을 고른다.

  1. 각 arm 별로 Gittins index를 계산한다.
  2. 가장 index가 높은 arm을 고른다.

Gittins index는 bandit problem을 풀기위한 초기 연구 중 하나로, 70 ~ 80년대에 연구된 결과이다. 이 방법론은 bandit 문제를 MDP로 취급하고 문제를 풀게 된다. 그냥 MDP만 사용하게 되면 문제를 풀기 위한 computation이 가능한 action의 모든 경우의 수와 bandit의 arm 개수의 exponential하게 증가하게 되기 때문에 Gittins는 이 문제를 해결하기 위하여 bandit problem이 n개의 1-D problem으로 reduce될 수 있음을 증명하고 각각의 1-D 문제의 계산 값을 Gittins index로 정의한 후, arm 중에서 가장 Gittins index가 높은 arm을 고르는 방법을 제안한다. 이 부분에서 Gittins index는 각 arm을 statistical distribution으로 생각하고 문제를 푸는 대신, 완전한 MDP문제로 해결하게 된다. 실제로는 별로 practical하지 않기에 쓰이지 않으며, UCB라고 하는 조금 더 practical한 approximation algorithm이 있기 때문에 보통 UCB를 사용하게 된다.

Algorithm 1: $\varepsilon$-greedy

Bandit problem을 푸는 가장 popular하면서도 간단한 알고리즘 중 하나로 $\varepsilon$-greedy라는 알고리즘이 있다. 이 알고리즘은 $1-\varepsilon$의 확률로 지금까지 관측한 arm 중에 가장 좋은 arm을 고르고 (exploitation), $\varepsilon$의 확률로 나머지 arm 중에서 random한 arm을 골라서 play하는 (explore) 알고리즘이다. 알고리즘은 다음과 같다.

  1. $1-varepsilon$의 확률로 지금까지 empirical reward가 가장 좋은 arm을 고른다.

  2. $varepsilon$의 확률로 uniformly random하게 arm을 고른다.

이 알고리즘은 뒤에서 설명할 다른 알고리즘들보다 이론적으로, 또 실험적으로 우수하지는 못하지만, 매우 직관적이다. 이 알고리즘의 parameter $\varepsilon$ 자체가 맨 처음 motivation으로 말했던 exploration and exploitation trade-off를 조절하는 term이 되기 때문이다. $\varepsilon$의 값이 크면 그만큼 exploration을 많이 하게 되고, 반대의 경우도 마찬가지로 생각할 수 있다. 이 알고리즘의 치명적인 단점을 몇 꼽자면, 먼저 시간이 많이 지나서 optimal한 arm이 무엇인지 알게 되었더라도 계속해서 $\varepsilon$만큼의 exploration을 해야하므로, optimal한 값과 멀어지는 결과를 낳게 된다는 점이다. 또 하나는 $\varepsilon$의 확률로 sub-optimal arm들을 뽑고, 그 마저도 uniformly random하게 뽑기 때문에, 전체 arm 중에서 관측하지 못하는, 혹은 관측을 많이 못해서 정보를 많이 얻게 되지 못하는 arm이 생기게 될 가능성이 크다는 것이다.

여러 문제들을 해결하기 위해서 $\varepsilon$을 constant로 사용하는 대신, adaptive하게 update하거나, 혹은 일정 비율로 감소시키는 방법론도 존재하며 $\varepsilon$-first 등의 variant algorithm 등도 역시 존재하지만 이 글에서는 다루지 않도록 하겠다.

Algorithm 2: UCB

앞서 설명한 $\varepsilon$-greedy는 항상 empirical mean이 좋은 arm만 고르고, 나머지를 $\varepsilon$의 확률로 고르지만, 실제로는 매 시간마다 arm $i$에서 얻는 보상은 constant가 아닌 특정 distribution에서 draw되는 random variable이기 때문에, 지금 empirical mean이 크다고 해서 정말로 그 arm이 늘 best일거라고 확신할 수 없다. 특히 관측 횟수가 적을 경우에는 empirical result와 실제 결과 간의 큰 차이가 발생할 확률이 높기 때문에 $\varepsilon$-greedy에는 심각한 결점이 있는 셈이다. 반대로 관측 횟수가 충분히 많다면 explore를 굳이 할 필요가 없음에도 $\varepsilon$ 만큼의 explore를 반드시 해야한다는 점 역시 문제가 된다.

UCB 알고리즘은 empirical mean이 가장 좋은 arm을 play하는 대신, 시간 t마다 과거의 관측결과(empirical mean과 관측 횟수)와 몇 가지 probabilistic한 계산들을 토대로구한 각각의 arm i의 upper confidence bound (UCB)를 구하고 이것이 가장 좋은 arm을 고르는 알고리즘이다. UCB를 간단히 설명하자면 그 동안의 관측 결과에서부터 time t에서 arm i의 expected reward의 confidence (확률이 높은) upper bound 정도로 설명할 수 있을 것이다. UCB 알고리즘은 매 시간 t에서 다음과 같은 rule로 arm i를 고른다.

  1. 다음 식을 만족하는 arm i를 고른다. $i = \arg\max_i \mu_i + P_i.$

뒤에 붙는 $P_i$ term이나 UCB를 정의하는 방법에 따라서 UCB1, UCB2, UCB-Tuned, MOSS, KL-UCB, Bayes-UCB 등의 variant가 있지만, 기본적인 아이디어는 동일하다고 생각하면 된다. 이론적으로 더 우수한 UCB를 가지게 될 경우 더 적은 regret을 가지게 되는데, 각각의 UCB variant 들에 대해서 이런 confidence bound를 증명한 work이 상당히 많이 있기 때문에 가장 좋은 UCB를 사용하면 된다. 이 글에서는 가장 간단한 UCB1만 소개를 해보도록 하겠다. UCB1의 policy는 다음과 같다.

$$i = \arg\max_i \bar x_i + \sqrt{\frac{2\ln t}{n_i}}.$$

여기에서 $\bar x_i$는 i번째 arm의 지금까지 관측한 평균 값이고, t는 현재 시간, $n_i$는 현재 시간에서 arm i가 play된 횟수를 의미한다. 이 값은 arm i의 실제 보상에 대한 $1-\frac{1}{t}$의 confidence의 upper bound로, Chernoff-Hoeffding bound를 통해 얻어지는 값이다. 처음에는 관측 결과가 좋은 arm을 고르되, 관측 결과가 적은 arm들을 고를 확률이 더 높을 수 있지만, 시간이 충분히 지나고나면 (time은 log scale이지만 관측은 linear scale이므로) empirical result가 더 큰 가중치를 얻게 되고, 그 결과 시간이 많이 지나고 나면 empirical하게 가장 좋은 arm 위주로 arm을 뽑게 된다.

UCB는 이론적으로 우수한 결과를 가지고 있고 (앞서 설명한 Gittins index의 아주 효율적인 appoximation algorithm이라는 것이 알려져 있다), 또한 실험에서도 잘 동작하는 것이 이미 알려져있지만 UCB 알고리즘도 만능은 아니다. UCB를 계산하기 위해서는 empirical mean이 필수적이기 때문에 반드시 처음에 모든 arm들을 explore해야한다는 이슈가 있기 때문에 초기에는 한 번 이상 exploration이 필요하다는 문제점이 있다.

Algorithm 3: Thompson Sampling

마지막으로 Thompson sampling, 혹은 probability matching에 대해 알아보자. 이 알고리즘은 google analytics에서도 사용하고 있는 알고리즘으로 [2] 최근 이론적인 증명과 실험적인 결과에서 모두 두각을 보이고 있는 알고리즘이다. [3], [4]

Thompson sampling의 기본 아이디어는 간단하다. 각각의 시간 t마다 policy에 따라 action a를 선택하고, 그에 상응하는 reward r을 받는다고 가정해보자. Thompson sampling은 observation $(a_t, r_t)$과 parameter $\theta$를 사용해 likelihood function $Pr[r ~|~ a, \theta]$를 설계한 다음, prior를 가정해 MAP 문제를 푸는 것이다. Arm의 i.i.d condition 등의 적절한 몇 가지 가정을 더하면, MAP 문제는 다음과 같이 기술된다.

$$\max_\theta Pr[\theta ~|~ D] = \prod Pr[r_t ~|~ a_t, x_t, \theta] Pr[\theta].$$

일반적인 경우, reward는 action a와 true parameter $\theta^*$에 대한 stochastic random variable이기 때문에, expected reward인 $\mathbb E[r~|~a,x,\theta^*]$를 maximize하는 방식으로 학습을 하게 된다. 여기에서 $\theta^*$이 unknown이기 때문에 다음과 같은 식을 maximize하는 action을 찾는 것이 더 합리적이다.

$$\mathbb E [r ~|~ a] = \int \mathbb E [r~|~a,\theta] Pr[\theta~|~D] d\theta.$$

이 문제를 풀기 위해서 probability mathing은 다음과 같은 heuristic을 사용하게 된다.

$$\int \mathbb I \left( \mathbb E [r~|~a,\theta] = \max_{a^\prime} \mathbb E [r~|~a^\prime,\theta] \right) Pr[\theta~|~D] d\theta.$$

여기에서 $\mathbb I(\cdot)$은 indicator function이다. 즉, 매 순간마다 전체 parameter에 대해서 가장 reward의 expectation을 maximize하는 action을 뽑는 방법이 된다. 이 방법에 따라 Thomson sampling algorithm은 다음과 같다. (x는 context vector라는 것인데, 지금은 무시해도 된다)

이때, 각각의 arm이 Bernoulli distribution을 따른다고 가정했을 때, 예전 글의 conjugate prior 설명에서 다뤘던 것 처럼, prior를 Beta distribution으로 잡았을 때 계산 상의 이점이 생긴다. Beta distribution Beta(a,b)는 $x^a (1-x)^b$를 normalize하는 형태로 생겼는데, a가 커질수록 관측될 확률이 높아지고 b가 커질수록 그 확률이 낮아진다. Thompson sampling에서는 a에는 arm을 play해서 성공한 횟수, b에는 arm을 play해서 실패한 횟수와 관련된 term을 assign함으로써 Beta distribution을 다음과 같이 정의하고 있다.

기본 아이디어도 어렵지 않고, 알고리즘 또한 엄청나게 간단한 편임에도 Thompson sampling은 다음 그래프에서 볼 수 있듯 UCB 등의 기존 알고리즘보다도 더 좋은 performance를 내는 것을 알 수 있다. ([3]에서 따옴)

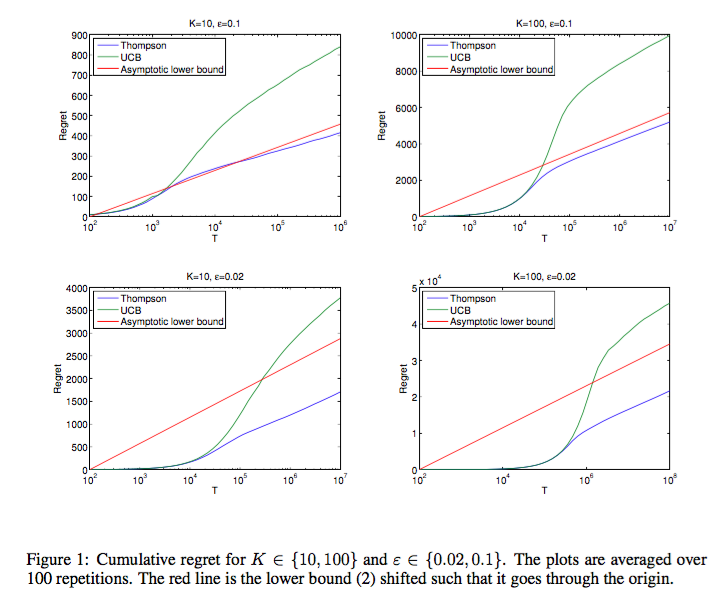
Thompson sampling의 장점 중 하나는, 한 번에 하나의 arm만 play하는 single play 문제에서 여러 개의 N개의 arm을 play할 수 있는 multi play 문제로의 확장이 용이하다는 것이다. 이 방법으로는 두 가지 방법이 있는데, 하나는 action을 maximization 문제를 만족하는 N개의 action을 순서대로 고르는 방법이 하나가 있으며 (Multiplay Thompson sampling, 줄여서 MP-TS), 또 다른 방법으로는 m-1개의 arm은 empirical result가 제일 좋은 arm을 고르고, 마지막 m번째 arm만 Thompson sampling으로 푸는 방법도 있다 (Improved MP-TS, 줄여서 IMP-TS). 흥미롭게도, 두 번째 방법이 실제로는 asymptotic bound를 유지하면서, 첫 번째 방법보다는 조금 더 나은 성능을 보인다고 한다. ([1]과 [4]에서 언급됨)

정리

이 글에서는 Multi-armed bandit problem에 대해 설명하고, 그 중 finite-armed stochastic multi-armed bandit problem을 푸는 네 가지 알고리즘에 대해 다뤘다. 현재 empirical하게 [3], (그리고 최근에는 theoretical하게까지 [4]) 가장 우수한 성능을 보이는 알고리즘은 Thompson sampling (arm의 prior를 Bernoulli distribution으로 가정했을 때)이다. 실제로는 위에서 설명한 bandit 보다 훨씬 더 복잡하고 어려운 bandit problem들이 많이 있으며 그것들을 해결하기 위한 알고리즘들 역시 많이 있지만, 이 글에서는 그런 variant들을 모두 다루기보다는, bandit을 이해하기 위해서 가장 필수적으로 이해하고 있어야할 요소들만 다루었다. 조금 더 advanced한 bandit들은 추후에 다른 글들을 통해 소개해볼 수 있도록 하겠다.

References

  1. Burtini, Giuseppe, Jason Loeppky, and Ramon Lawrence. “A Survey of Online Experiment Design with the Stochastic Multi-Armed Bandit.”, 2015.
  2. Google Anayltics Help - multi-armed bandit computational and theoretical details
  3. Chapelle, Olivier, and Lihong Li. “An empirical evaluation of thompson sampling.”, 2011.
  4. Komiyama, Junpei, Junya Honda, and Hiroshi Nakagawa. “Optimal regret analysis of thompson sampling in stochastic multi-armed bandit problem with multiple plays.”, 2015.

변경 이력

  • 2016년 3월 13일: 글 등록

Machine Learning 스터디의 다른 글들