들어가며
Machine learning 문제를 풀다보면 Objective function을 만들고 그 objective function을 optimize 해야하는 경우가 매우 빈번하게 발생한다. 간단히 생각해서 loss function을 minimize하는 것도 optimization이다. 그렇다면 그런 optimization은 도대체 어떻게 해야하는 것일까. 여러가지 방법이 있겠지만 이번 글에서는 간단한 optimization이라는 것에 대한 컨셉을 다루고, 그 중 특수 케이스인 convex optimization에 대해 다루도록 하겠다.
Optimization
대부분의 Optimization은 아래와 같은 식으로 표현할 수 있을 것이다.
$$ \min f(x) \text{ s.t. } g(x) = c $$
여기에서 $f(x), g(x)$는 함수이다. 어떤 함수의 optimum point, 즉 그것이 최소이거나 혹은 최대인 지점을 찾는 과정을 optimization이라고 한다고 생각하면 간단할 것이다. 엄청 간단하게 생각해보면 $f(x)$는 loss function이고, $g(x)$는 일종의 constriants로 생각하면 될 것 같다. Machine learning 문제를 풀다보면 이렇게 optimization을 해야하는 일이 아주 빈번하게 발생하는데, 안타깝게도 항상 이런 function들의 optimum point를 찾을 수 있는 것은 아니다. 가장 간단하게 생각했을 때 이런 point를 찾는 방법은 미분을 하고 그 값이 0이 되는 지점을 찾는 것인데, 안타깝게도 미분 자체가 되지 않는 함수가 존재할 수도 있으며, 미분값이 0이라고 해서 반드시 극점인 것은 아니기 때문이다. (saddle point를 생각해보자.) 따라서 대부분의 경우에 이런 방법으로 극점을 구하는 것은 불가능하며, 매우매우 특수한 일부 경우에 대해서 완전한 optimum을 찾는 것이 알려져 있다. 그리고 그 경우가 바로 convex optimization이다.
Convex function
Convex function은 convex한 function을 의미한다. 이때 convex는 한국어로 옮기면 볼록에 가까운데, convex function은 볼록 함수라고 번역할 수 있다. Convex가 무슨 의미인지 차근차근 알아보자. 먼저 convex set에 대해 알아보자. 어떤 set이 convex하다는 것의 의미는 그 set에 존재하는 그 어떤 점을 잡아도 그 점들 사이에 있는 모든 점들 역시 그 set에 포함되는 set을 알컬어 convex set이라고 부른다. 따라서 convex한 set을 그림으로 그리게 되면 움푹하게 파인 지점 없이 약간 동글동글한 모양을 하고 있을 것이다. 그렇다면 이제 convex function을 정의해보자. Convex function은 domain이 convex set이며, 함수는 다음과 같은 성질을 만족해야한다.
$$ f(\lambda x_1 + (1-\lambda x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)) \text{ for } \forall x_1, x_2 \in X, \forall \lambda \in [0,1] $$
즉, 아래와 같은 함수는 convex function이다.
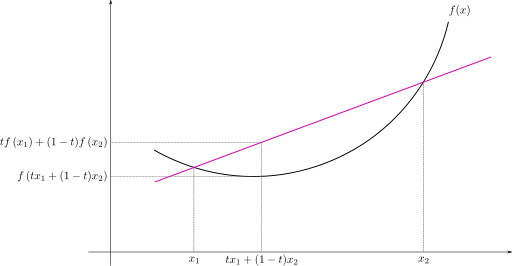
Convex function이 좋은 이유는 반드시 optimal한 값이 하나 밖에 존재하지 않는다는 것이다. 여기에서 내가 optimal point가 하나라고 얘기하지 않은 이유는 아래와 같은 예가 있기 때문이다.
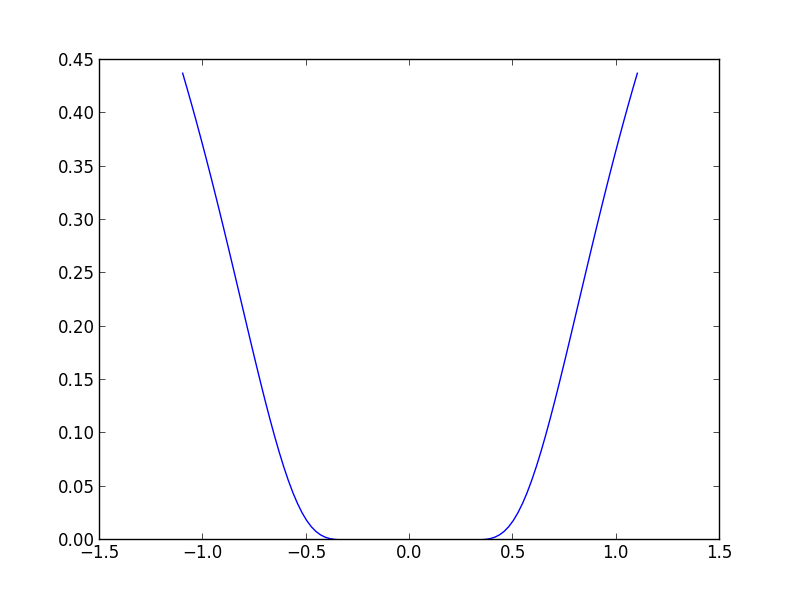
이 함수는 optimal한 값은 unique하게 존재하지만, 그 값을 가지는 point가 unique하지는 않다.
따라서 unique한 optimal point를 찾기 위해서는 하나의 조건이 더 필요한데, 바로 strictly convex라는 조건이다. 이 조건은 위의 식에서 = 이 빠진 형태이다. 즉 ≤ 가 < 으로 바뀌는 것이다.
이런 strictly convex function에 대해서 optimal point가 unique하게 존재한다는 것을 증명할 수 있으며, 증명과정은 크게 어렵지 않으니 링크 등을 참고하면 될 것 같다. 아무튼 strictly convex function은 minimum point가 unique하게 존재하기 때문에, 이런 convex function에 대해서 우리는 어떤 optimization algorithm을 design할 수 있다.
Convex Optimization
Convex function $f, g_1, g_2, …, g_m$에 대해 아래와 같은 optimization 문제를 Convex optimization이라 정의한다.
$$ \min f(x) \text{ subject to } g_i (x) \leq 0, \text{ i = 1,…,m}$$
모든 함수들이 convex하기 때문에 이 optimization의 solution은 unique하며, 이런 optimization 문제를 풀 수 있는 방법은 아주아주 많이 존재한다.
이런 convex optimization의 subset으로 linear programming, quadratic programming, semidefinite programming 등이 존재한다. 이 글에서는 그런 특수한 경우는 다루지 않고, 일반적인 convex optimization에서 사용할 수 있는 알고리듬들을 다룰 예정이다. 크게 gradient descent method, newton method, 그리고 lagrange multiplier가 그것이다.
Gradient Descent Method
Gradient Descent Method는 미분 가능한 convex function의 optimum point를 찾는 가장 popular한 방법 중 하나이다. 장점이라면 많은 application에 implement하기 매우 간단하고, 모든 차원과 공간으로 확장할 수 있으며, 수렴성이 항상 보장된다는 것이지만, 속도가 느리다는 단점이 존재한다.
아이디어는 매우 간단하다. 어떤 산 위에 우리가 서있다고 가정해보고 우리가 알 수 있는 정보는 내 위치와 내 주변 위치들의 높이 차이밖에 없다고 가정해보자. 만약 내가 산의 가장 낮은 위치로 내려가야하는 상황이라면 어떻게 내려가면 낮은 위치에 도달할 수 있을까? 가장 간단한 방법은 가장 기울기가 가파른 방향을 골라서 내려가는 것이다. 그러다보면 언젠가는 기울기가 0이 되는 지점에 도달하게 될 것이고, 그 지점이 주변에서는 가장 낮은 지점이 될 것이다. 만약 산의 높이가 convex function이라면, 즉 가장 낮은 지점이 unique하다면, 그렇게 도달한 지점이 우리가 원했던 가장 optimal한 지점이라는 것을 알 수 있다. 즉, 이 알고리듬은 매 step마다 현재 위치에서의 가장 가파른 아래로 내려가는 기울기 $-\nabla f(x^{(k)})$를 계산하고, 그 방향으로 이동하고, 다시 기울기를 계산하는 방식의 iterative algorithm이다.
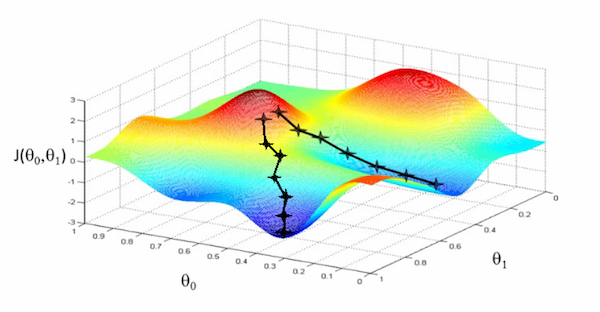
Algorithm description은 다음과 같다.
$$ x^{(k+1)} = x^{(k)} - \eta^{(k)} \nabla f(x^{(k)}) $$
이 때 $x^{(k)}$ 는 k번 째 iteration에서의 x의 값이며 $\nabla f(x^{(k)})$ 는 그 지점에서의 gradient 값이다. 이를 조금 더 알고리듬스럽게 기술해보면
- set iteration counter k=0, and make an initail guess $x_0$ for the minimum
- Compute $-\nabla f(x^{(k)})$
- Choose $\eta^{(k)}$ by using some algorithm
- Update $x^{(k+1)} = x^{(k)} - \eta^{(k)} \nabla f(x^{(k)}))$ and k = k+1
- Go to 2 until $\nabla f(x^{(k)})) < \epsilon $
만약 function이 convex하다면, 이런 방법으로 x를 계속 update하다보면 적절한 $\eta$를 취했을 때 이 algorithm은 global unique optimum으로 수렴하게 된다. 이때 $\eta$를 Step size라고 일컫는데, 이 step size를 어떻게 설정하느냐에 따라 알고리듬의 performance가 좌우된다. 만약 step size가 너무 작다면 iteration을 너무 많이 돌아서 전체 performance자체가 저하될 것이다. 그렇다고 step size가 너무 크다면 minima에 converge하는 것이 아니라 그 주변에서 diverge를 할 수도 있다.
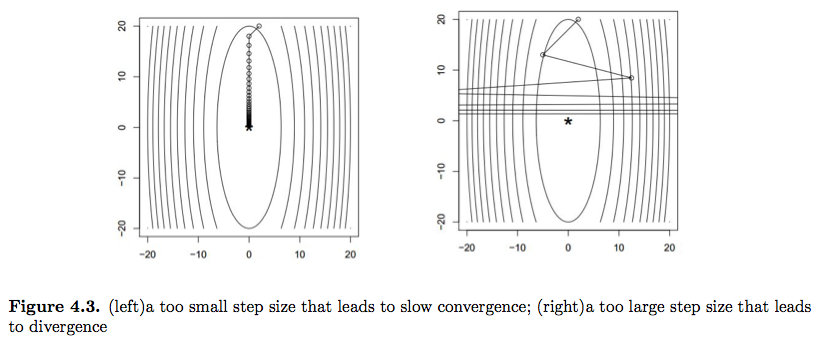
Step size를 고르는 방법은 크게 fixed step size를 취하는 방법과 매번 optimal한 step size를 고르는 방법 두 가지가 존재한다. 먼저 fixed step size에 대해 살펴보자.
앞서 언급했듯, step size를 잘 잡는 것이 중요한데, 너무 큰 step size를 잡게 되면 algorithm이 diverge 하기 때문이다. 다행히도 우리는 어떤 적절한 step size $\eta$에 대해 algorithm이 strictly convex function f의 global unique optimum으로 수렴한다는 증명을 할 수 있다.
이 적절한 step size에 대해 설명을 하려면 먼저 L-Lipschitz function이라는 것을 정의해야하는데, 이는 다음과 같이 정의된다.
$$ \|\nabla f(x) - \nabla f(y) \|_2 \leq L \|x-y\|_2, \forall x,y \in R^n $$
만약 f가 L-Lipschitz function이고 어떤 optimum이 존재한다면 fixed step size $\eta \leq \frac{2}{L}$ 을 취했을 때 gradient descent algorithm이 stationary point로 수렴하게 된다는 것을 증명할 수 있다. 증명은 이 렉쳐노트를 참고하기를 바란다.
다음으로 step size를 계속 update하는 방식(이를 Line search라고 한다)을 살펴보자.
먼저 exact line search라는 것 부터 살펴보자. Exact line search의 algorithm은 다음과 같다
- set iteration counter k=0, and make an initail guess $x_0$ for the minimum
- Compute $-\nabla f(x^{(k)})$
- Choose $\eta^{(k)} = argmin_\eta f(x^{(k)} - \eta \nabla f(x^{(k)}))$
- Update $x^{(k+1)} = x^{(k)} - \eta^{(k)} \nabla f(x^{(k)}))$ and k = k+1
- Go to 2 until $\nabla f(x^{(k)})) < \epsilon $
이 알고리듬은 가장 optimal한 $\eta$를 매 순간 찾아준다. 하지만 이 알고리듬은 3번 과정 때문에 practical하지는 못하고, 이 알고리듬을 조금 더 practical하게 보완한 backtracking line search algorithm이 조금 더 많이 쓰인다.
For $\alpha \in {0, 0.5}, \beta \in {0,1}$
- set iteration counter k=0, and make an initail guess $x_0$ and choose initial $\eta=1$
- Compute $-\nabla f(x^{(k)})$
- Update $\eta^{(k)} = \beta \eta^{(k)}$
- Go to 2 until $f(x^{(k)} - \eta^{(k)} \nabla f(x^{(k)}))) \leq f(x^{(k)}) - \alpha \eta^{(k)} \| \nabla f(x^{(k)})) \|^2 $
- Update $x^{(k+1)} = x^{(k)} - \eta^{(k)} \nabla f(x^{(k)}))$ and k = k+1
- Go to 1 until $\nabla f(x^{(k)})) < \epsilon $
보통 $\alpha$는 0.01에서 0.3 사이의 값으로 선택하고 $\beta$의 값은 0.1에서 0.8 정도로 설정된다.
이론적으로는 line search 쪽이 convergence speed가 훨씬 빠르지만, 실제로는 이를 구하는 것보다 적당한 step size로 값을 고정해놓고 gradient descent를 취하는 방법이 더 쉽고, line search를 위해 update되는 step size에 소모되는 computation이 꽤 크기 때문에 practical하게는 적당한 step size를 고정하는 방법이 훨씬 더 많이 사용된다.
Gradient Descent를 약간 응용하여 변형한 알고리듬으로는 Coordinate Descent method, Steepest descent method 등이 존재한다.
간단하게 개념만 설명하자면, Coordinate descent는 각 좌표계 방향에서 한 방향씩으로만 번갈아가면서 gradient descent를 하는 것이다. 예를 들어 n차원 function이 있는 경우, 첫번째 차원에 대해 gradient descent를 계산하고 두번째 세번째.. n번째 차원에 대해 이 과정을 반복한다. 그리고 이 과정을 전체 함수가 converge할 때 까지 반복한다. 이 방법이 좋은 이유는 함수가 비록 convex하지 않더라도, 어떤 특수한 경우에 대해 이 방법을 사용해 optimal point를 얻을 수 있기 때문이다.
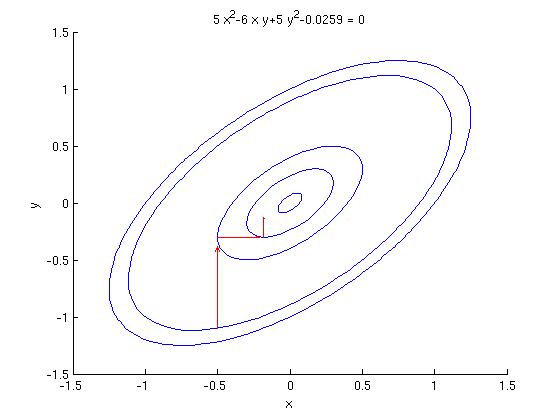
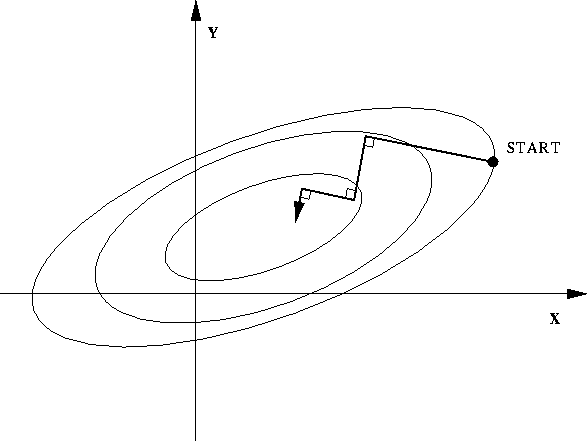
Steepest descent는 간단히 생각하면 norm을 적절한 norm으로 바꿔 더 빠르게 converge를 시키는 방법이다. 이 방법은 saddle point가 존재하는 경우에 유용하게 사용할 수 있다고 한다.
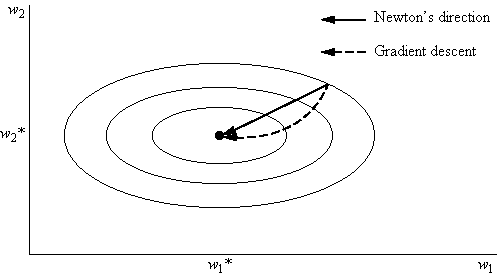
Newton’s Method
Gradient descent는 기울기 정보 즉, 미분을 한 번만 한 값만을 사용하는데 만약 우리가 두 번 미분한 값을 사용할 수 있다면 훨씬 훨씬 빠른 수렴속도를 보이는 알고리듬을 디자인할 수 있을 것이다. Newton’s method는 Gradient Descent의 2nd derivative version으로 훨씬 수렴성이 빠르다는 장점을 가지고 있지만, Hessian Matrix를 계산해야하기 떄문에 computation과 memory측면에서 expensive하다는 단점을 가지고 있다.
2번 미분 가능한 strongly convex function f에 대해 Newton step은 다음과 같이 기술된다.
$$ \triangle x_{nt} (x) = -\nabla^2 f(x)^{-1} \nabla f(x) $$
이 newton step에 대해 newton’s method 알고리듬은 다음과 같이 쓸 수 있다.
- initialize
- Compute the newton step $\triangle x = -\nabla^2 f(x)^{-1} \nabla f(x)$
- Choose step size $\eta$
- Update $x^+ = x + \eta \triangle x_{nt} (x) $
- Go to 2 until converge
이 알고리듬을 깊게 파고들어가면 할 얘기가 정말 많아지므로 일단 convergence 조건이나, step size를 고르는 방법 등에 대해서는 생략하도록 하겠다. 하지만 이 알고리듬에 대해 크게 두 가지 얘기는 꼭 하고 넘어가야할 것 같은데, 하나는 convergence speed, 그리고 하나는 computation이다.
먼저 이 알고리듬은 매우 빠르게 수렴한다. 실제 convergence rate를 증명했을 때 gradient descent보다 빠르게 수렴할 뿐더러, 실제 practical하게도 (Hessian을 계산할 수 있다면) 아래와 같은 convergence phase를 보인다

즉 처음에는 linear하게 converge하는 것처럼 보이지만, 시간이 지나면 순식간에 quadratic으로 수렴한다. 생각해보면, newton method는 기울기 뿐 아니라, 기울기의 기울기 정보도 같이 사용하기 때문에, 처음에 기울기가 크게 변하지 않을 때는 빠르게 감소하다가, 갑자기 기울기의 크기가 변하기 시작하면 그에 맞춰서 적절한 newton step을 찾을 수 있기 때문에 아주 빠르게 수렴할 수 있다. 특히 saddle point에 대해 영향을 크게 받지 않기 때문에 gradient descent 보다는 훨씬 훨씬 빠르게 수렴한다.
하지만 Newton method의 근본적인 한계는 바로 Hessian을 계산해야한다는 점이다. 이 Hessian을 계산하는 것 자체도 매우 연산이 복잡할 뿐 아니라, gradient의 제곱 만큼의 공간이 필요하기 때문에 memory 역시 efficient하게 사용하기가 어렵다. 때문에 매우 복잡한 함수에 대해서는 newton method를 사용하기가 매우 힘들다. 예를 들어서 neural network에서 gradient descent method를 사용하면 chain rule을 통해 아주 쉽게 그 값을 계산할 수 있지만, second derivation으로 넘어가는 순간, computation을 해야할 양이 급격하게 증가하고, 안그래도 부족한 메모리가 더 부족하게 되기 때문에 neural network에서는 사용되지 않는 방법이다.
대략 요약하자면, 별 일이 없다면 gradient descent에서 fixed step size를 사용해 converge를 시키는 것이 practical하게는 가장 많이 쓰이고 있다. 하지만, 더 빠른 convergence speed가 필요하다면 line search나 steepest method, newton’s method를 한 번쯤은 고려해볼만 할 것이다.
Lagrange Multiplier
마지막으로 Lagrange multiplier에 대해 살펴보자. Lagrange Multiplier는 constrained optimization을 푸는 매우 popular한 방법 중 하나이다. 원리는 원래 constrained optimization과 같은 optimum point를 가지는 새로운 unconstrained optimization 문제를 만들어서 optimum point를 구하는 것이다. 즉, 다음과 같은 optimization 을 생각해보자
$$ \min f(x) \text{ s.t. } g(x) = c $$
그렇다면 이와 같은 극점을 가지는 다음과 새로운 optimization problem을 만드는 상수 $\lambda$가 존재한다.
$$ \min f(x) + \lambda (g(x) - c) $$
보통 c는 상수이기 때문에 극값에 영향을 주지 않으므로 많이 무시된다.
이 문제를 푸는 방법은 여러 개가 있지만, 어렵지 않은 문제인 경우 Lagrange function을 편미분해 0이 되는 값들을 모두 구해 $\lambda$를 계산해 대입해서 극값을 찾는 방법을 많이 취한다.
하지만 편미분을 구하기 어려운 경우도 존재하기 때문에 항상 그렇게 푸는 것은 아니고, 이런 문제를 잘 풀 수 있는 여러 알고리듬들이 존재하며, 최근 많이 쓰이는 알고리듬으로는 ALM (Augumented Lagrange method)가 있다.
Lagrange Multiplier는 풀기 어려운 constrained optimization problem을 그보다 더 풀기 쉬운 unconstrained optimization problem으로 바꿔주기 때문에, 새로운 Lagrange function을 풀기 쉬운 경우에 많이 사용한다.
Optimization for non-convex function (Local optimum)
하지만 위에서 서술한 방법들은 오직 convex한 function에만 적용할 수 있는 방법들이므로 우리는 non convex한 함수들은 optimize할 수 없다.. 라고 말해야하지만, 사실 꼭 그렇지만은 않다. Convex function은 global optimum, 즉 해당 식을 만족하는 x를 반드시 찾을 수 있지만, 같은 방법을 적용했을 때 non-convex한 함수는 그럴 수 없다. 하지만 non-convex한 함수이더라도 local optimum 값을 찾을 수는 있다. 때문에 많은 경우에 optimization problem이 convex하지 않다고 하더라도 converge를 하는 것 만으로도 그 문제를 풀었다라고 얘기하는데, 이때, local하게 함수를 봤을 때 convex하다면 gradient descent 등의 방법을 사용해서 local optimum을 계산할 수 있다. 예를 들어서 Neural network에 많이 쓰이는 backpropagation algorithm은 사실 gradient descent method algorithm인데, 따라서 이 알고리듬의 결과는 항상 local optimum으로 converge한다.
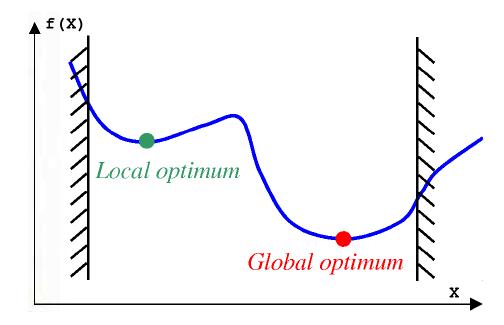
따라서 convex하지 않은 optimization일지라하더라도, 일단은 gradient descent 등의 방법을 통해 optimization을 할 수 있다면, local optimum을 구할 수 있다.
하지만 그럼에도 local한 optimum이 엄청나게 많은 경우에는 local optimum으로 converge하는 것이 문제가 되기 때문에 함수를 convex하게 relaxation 시켜서 optimization을 푸는 경우도 존재한다. 특히 원래 문제가 NP-hard인 경우, parameter를 골라야하는 경우 등에 convex relaxation을 많이하는 것 같다.
Reference
- Convex optimization by Boyd
- Lecture slides by Boyd and Vandenberghe
- EE381V - Large Scale Optimization The University of Texas at Austin
변경 이력
- 2014년 9월 10일: 글 등록
- 2015년 2월 28일: 변경 이력 추가
Machine Learning 스터디의 다른 글들
- Machine Learning이란?
- Probability Theory
- Overfitting
- Algorithm
- Decision Theory
- Information Theory
- Convex Optimzation
- Classification Introduction (Decision Tree, Naïve Bayes, KNN)
- Regression and Logistic Regression
- PAC Learning & Statistical Learning Theory
- Support Vector Machine
- Ensemble Learning (Random Forest, Ada Boost)
- Graphical Model
- Clustering (K-means, Gaussian Mixture Model)
- EM algorithm
- Hidden Markov Model
- Dimensionality Reduction (LDA, PCA)
- Recommendation System (Matrix Completion)
- Neural Network Introduction
- Deep Learning 1 - RBM, DNN, CNN
- Reinforcement Learning