들어가며

EM 알고리즘은 latent variable이 존재하는 probabilistic model의 maximum likelihood 혹은 maximum a posterior 문제를 풀기 위한 알고리즘 중 하나이다. 굉장히 많은 probabilistic 모델을 풀기 위해 널리 사용되는 알고리즘 중 하나이며, iterative한 알고리즘 중 하나이다. Clustering에서 다뤘던 GMM은 물론이고, HMM, RBM 등의 문제를 해결하는데 있어서도 사용되는 알고리즘이다. 이 글에서는 EM 알고리즘이 무엇인지, latent variable이 존재하는 probabilistic model은 무엇이며 어떤 장점이 있는지를 다룰 것이며, EM 알고리즘의 의미와 더 나아가 이 알고리즘이 어떻게 MLE나 MAP문제를 해결하는지에 대해 다룰 것이다.

Probabilistic model having latent variable

EM 알고리즘에 대해 다루기 전에 먼저 latent variable을 가지고 있는 probabilistic model에 대해 설명하도록 하겠다. Latent variable은 우리가 본래 가지고 있는 random variable이 아닌, 우리가 임의로 설정한 hidden variable을 의미한다. 예를 들어, 아래 그림과 같은 Grapical model을 고려해보자. 이때 우리가 관측할 수 있는 random variable은 paramter $\theta$로 parameterized 되어있는 $\mathbf X$ 하나이고, $\mathbf Z$은 우리가 관측할 수 없는 hidden variable이라고 해보자.

만약 위의 grapical model에서 $\mathbf X$의 maximum likelihood를 계산하고 싶다면 어떻게 해야할까? 먼저 $\mathbf X$의 maximum likelihood는 다음과 같이 표현된다.

$$\max_{\theta} p(\mathbf X | \theta) = \sum_{\mathbf Z} p(\mathbf X,Z | \theta). $$

문제를 조금 더 간단하게 하기 위하여 위의 식에서 $\mathbf Z$는 discrete variable이라고 정의하였다. 이 문제에서 우리가 가정할 것이 하나있다. 바로 marginal distribution $p(\mathbf X | \theta)$를 직접 계산하는 것이 매우 까다롭다는 것이다. 이때, $\mathbf Z$는 우리 마음대로 정할 수 있는 latent variable이기 때문에, joint distribution $p(\mathbf X,Z | \theta)$가 marginal distribution보다 쉬운 $\mathbf Z$를 잡는 것이 가능하다.

Decomposition of log-likelihood

만약 우리가 latent variable $\mathbf Z$의 marginal distribution을 $q(\mathbf Z)$라고 정의한다면, 앞에서 설명한 log-likelihood를 다음과 같이 decompose할 수 있다.

$$\ln p(\mathbf X | \theta) = \mathcal L(q,\theta) + ~\mbox{KL}(q\|p),$$ 이때, $\mathcal L(q,\theta)$와 $\mbox{KL}(q\|p)$는 다음과 같이 정의된다. $$\mathcal L(q,\theta) = \sum_{\mathbf Z} q(\mathbf Z) \ln \frac{p(\mathbf X, \mathbf Z | \theta)}{q(\mathbf Z)} ~\mbox{and}~ \mbox{KL}(q\|p) = - \sum_{\mathbf Z} q(\mathbf Z) \ln \frac{p(\mathbf Z | \mathbf X, \theta)}{q(\mathbf Z)}. $$

위의 식에서 $\mathcal L(q,\theta)$는 hidden variable $\mathbf Z$의 marginal distribution $q(\mathbf Z)$의 functional이고, $\mbox{KL}(q\|p)$는 $q,p$의 KL divergence를 의미한다. 이렇게 log-likelihood를 decompose하게 되면, 한 쪽에는 random variable $\mathbf X, \mathbf Z$의 joint distribution, 그리고 또 한 쪽은 conditional distribution으로 표현이 된다는 것을 알 수 있다. 또한 KL divergence의 특성에서부터 재미있는 사실을 하나 더 유추할 수 있는데, 바로 KL divergence가 반드시 0보다 크거나 같기 때문에 $\mathcal L(q,\theta)$이 곧 log-likelihood의 lower bound가 된다는 사실이다. 이를 그림으로 나타내면 아래 그림의 오른쪽 그림과 같다. (일단 $theta^{\mbox{old}}, theta^{\mbox{new}}$는 무시하자)

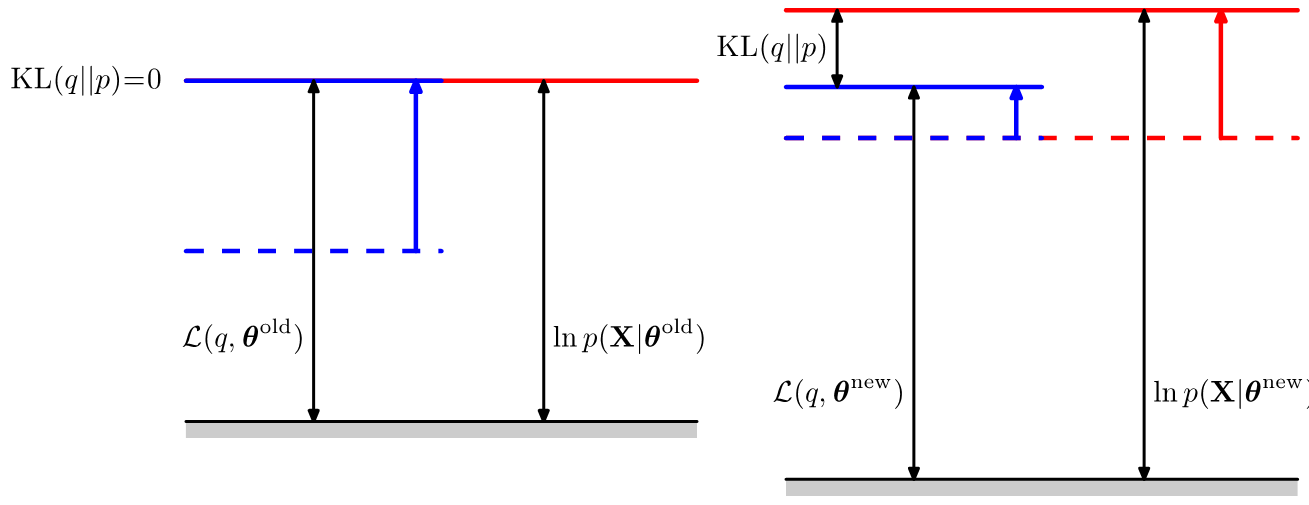
EM algorithm

위와 같은 사실로부터 lower bound가 maximum이 되도록하는 $\theta$와 $q(\mathbf Z)$의 값을 찾고, 그에 해당하는 log-likelihood의 값을 찾는 알고리즘을 설계하는 것이 가능할 것이다. 만약 $\theta$와 $q(\mathbf Z)$를 jointly optimize하는 문제가 어려운 문제라면 이 문제를 해결하는 가장 간단한 방법은 둘 중 한 variable을 고정해두고 나머지를 update한 다음, 나머지 variable을 같은 방식으로 update하는 alternating method일 것이다. EM 알고리즘은 이런 아이디어에서부터 시작하게 된다. EM 알고리즘은 E-step과 M-step 두 가지 단계로 구성된다. 각각의 step에서는 앞서 설명한 방법처럼 $\theta$와 $q(\mathbf Z)$를 번갈아가면서 한 쪽은 고정한채 나머지를 update한다. 이런 alternating update method는 한 번에 수렴하지 않기 때문에, EM 알고리즘은 E-step과 M-step을 알고리즘이 수렴할 때 까지 반복하는 iterative 알고리즘이 된다.

현재 우리가 가지고 있는 parater $\theta$의 값을 $\theta^{\mbox{old}}$라고 정의해보자. EM 알고리즘의 E-step은 먼저 $\theta^{\mbox{old}}$ 값을 고정해두고 $\mathcal L(q,\theta)$의 값을 최대로 만드는 $q(\mathbf Z)$의 값을 찾는 과정이다. 이 과정은 매우 간단하게 계산 수 있는데, 그 이유는 log-likelihood $\ln p(\mathbf X | \theta^{\mbox{old}})$의 값이 $q(\mathbf Z)$ 값과 전혀 관계가 없기 때문에, 항상 $\mathcal L(q,\theta)$를 최대로 만드는 조건은 KL divergence가 0이 되는 상황이기 때문이다. KL divergence는 $q(\mathbf Z) = p(\mathbf Z | \mathbf X, \theta^{\mbox{old}})$ 인 상황에서 0이 되기 때문에, $q(\mathbf Z)$에 posterior distribution $p(\mathbf Z | \mathbf X, \theta^{\mbox{old}})$을 대입하는 것으로 해결할 수 있다. 따라서 E-step은 언제나 KL-divergence를 0으로 만들고, lower bound와 likelihood의 값을 일치시키는 과정이 된다.

E-step에서 $\theta^{\mbox{old}}$을 고정하고 $q(\mathbf Z)$에 대한 optimization 문제를 풀었으므로 M-step에서는 그 반대로, $q(\mathbf Z)$를 고정하고 log-likelihood를 가장 크게 만드는 새 paramter $\theta^{\mbox{new}}$을 찾는 optimization 문제를 푸는 단계가 된다. E-step에서는 update하는 variable과 log-likelihood가 서로 무관했기 때문에 log-likelihood가 증가하지 않았지만, M-step에서는 $\theta$가 log-likelihood에 직접 영향을 미치기 때문에 log-likelihood 자체가 증가하게 된다. 또한 M-step에서 $\theta^{\mbox{old}}$가 $\theta^{\mbox{new}}$로 바뀌었기 때문에 E-step에서 구했던 $p(\mathbf Z)$로는 더 이상 KL-divergence가 0이 되지 않는다. 따라서 다시 E-step을 진행시켜 KL-divergence를 0으로 만들고, log-likelihood의 값을 M-step을 통해 키우는 과정을 계속 반복해야만한다.

위에 나왔던 그림에서 왼쪽이 E-step을 의미하고, 오른쪽 그림이 M-step을 의미한다. E-step을 의미하는 왼쪽 그림에서 KL divergence는 0이 되고, lower bound인 functional과 log-likelihood의 값이 같아진다. 오른쪽 그림은 M-step을 표현하고 있으며, $\theta$가 update되면서 log-likelihood의 값이 증가하게 되지만, 더 이상 KL divergence의 값이 0이 아니게 된다. 이 과정을 더 이상 값이 변화하지 않을 때 까지 충분히 많이 돌리게 되면 이 값은 log-likelihood의 어떤 값으로 수렴하게 될 것이다. 그리고 매 step마다 항상 optimal한 값으로 진행하기 때문에 이 값은 log-likelihood의 local optimum으로 수렴하게 된다는 사실까지 알 수 있다. EM algorithm은 아래와 같은 그림으로 표현할 수 있다.

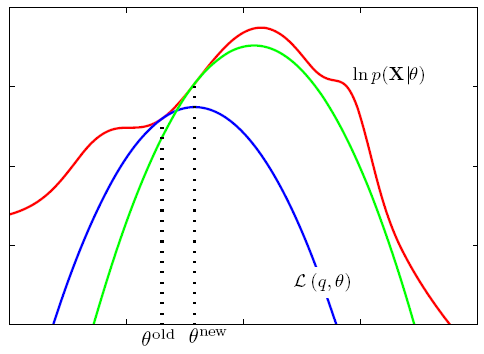
각 curve는 $\theta$ 값이 고정이 되어있을 때 $q(\mathbf Z)$에 대한 lower bound $\mathcal L(q,\theta)$의 값을 의미한다. 매 E-step마다 고정된 $\theta$에 대해 $p(\mathbf Z)$를 풀게 되는데, 이는 곧 log-likelihood와 curve의 접점을 찾는 과정과 같다. 또한 M-step에서는 $\theta$ 값 자체를 현재 값보다 더 좋은 지점으로 update시켜서 curve 자체를 이동시키는 것이다. 이런 과정을 계속 반복하면 알고리즘은 언젠가 local optimum으로 수렴하게 될 것이다. Local optimum에 수렴한다는 성질은 얼핏보면 나빠보일 수도 있지만, 이 글의 도입부에서 latent variable이 introduce되는 이유 자체가 원래 log-likelihood를 계산하는 것이 불가능에 가깝기 때문이었다는 사실을 돌이켜본다면, latent variable을 잘 잡기만 한다면 반드시 local optimum으로 수렴하는 EM 알고리즘은 매우 훌륭한 알고리즘이라는 사실을 알 수 있다. 즉, 아예 문제를 풀지 못하는 것 보다는 local optimum으로 수렴하는 것이 훨씬 좋다.

Pratical issues

대부분의 probabilistic model의 MLE 혹은 MAP는 EM 알고리즘을 사용하면 구할 수 있다. 그러나 EM 알고리즘이 항상 잘 동작하는 것은 아닌데, E-step 혹은 M-step의 optimization 문제를 푸는 것이 어려운 상황이 그러하다. E-step은 posterior를 계산하는 과정이므로 크게 문제가 되는 경우는 많지 않지만, M-step은 $\theta$에 대한 optimization 문제를 풀어야하는 과정인데, 이 과정에서 문제가 발생하는 경우가 많다. 예를 들어 모든 $\theta$를 한 번에 jointly optimize하는 것이 어려워 또 다른 alternative method를 사용해야할 수 도 있다. 그렇게 되면 iterative 알고리즘 안에 nested iterative 알고리즘이 발생하게 되어 전체 알고리즘의 수렴 속도가 매우 느려지게 된다. 가장 단순하게 이 문제를 해결하는 방법으로는 nested iterative 알고리즘을 완전히 푸는 것이 아니라, 수렴여부와 관계없이 iteration을 조금만 돌리고 다시 E-step을 구하고, 다시 M-step을 정확히 푸는 대신 iteration을 몇 번만 돌리는 등의 방식이 있을 것이다. 일반적인 경우에는 이런 방식이 수렴하지 않지만, 몇몇 경우에는 이런 방식이 local optimum에 수렴한다는 것이 증명되어있다. 가장 대표적인 예가 RBM을 푸는 Contrastive Divergence이다. 이에 대한 더 자세한 설명은 추후에 Deep learning에 대해 다루는 글에서 더 자세히 다루도록 하겠다.

정리

EM 알고리즘은 latent variable이 존재하는 probabilistic model의 maximum likelihood 혹은 maximum a posterior 문제를 풀기 위한 알고리즘 중 가장 대표적인 알고리즘이다. 본문에서는 MLE를 계산하는 과정만 다뤘지만, MAP도 비슷한 방식으로 구할 수 있다. Latent variable을 쉽게 잡기만한다면, 아무리 풀기 어려운 문제일지라도 구하고자 하는 문제의 local optimum에 수렴한다는 좋은 성질을 가지고 있기 때문에 매우 다양한 모델에서 이 알고리즘을 사용해 문제를 해결하고는 한다. 그러나 간혹 특히 M-step의 optimization을 푸는 과정에서 시간이 너무 오래 걸리는 문제가 발생하는 경우가 생길 수 있는데, 이런 경우 몇 가지 휴리스틱을 사용해 문제를 해결하기도 한다.

Reference

• Bishop, Christopher M. Pattern recognition and machine learning. Vol. 4. No. 4. New York: springer, 2006. Chapter 9

변경 이력

• 2015년 6월 14일: 글 등록

---

Machine Learning 스터디의 다른 글들

• Machine Learning이란?
• Probability Theory
• Overfitting
• Algorithm
• Decision Theory
• Information Theory
• Convex Optimzation
• Classification Introduction (Decision Tree, Naïve Bayes, KNN)
• Regression and Logistic Regression
• PAC Learning & Statistical Learning Theory
• Support Vector Machine
• Ensemble Learning (Random Forest, Ada Boost)
• Graphical Model
• Clustering (K-means, Gaussian Mixture Model)
• EM algorithm
• Hidden Markov Model
• Dimensionality Reduction (LDA, PCA)
• Recommendation System (Matrix Completion)
  • Recommendation System with Implicit Feedback
• Neural Network Introduction
• Deep Learning 1 - RBM, DNN, CNN
• Reinforcement Learning
  • Multi-armed Bandit