들어가며

이 글에서는 recommendation 문제가 어떤 문제인지에 대해 간략하게 설명하고, 각각을 푸는 가장 대표적인 알고리즘인 matrix factorization에 대해서 설명할 것이다. 이 글의 많은 부분이 예전에 적었던 글 [1], [2]을 기반으로 작성하였으니, 궁금하다면 추가로 읽어보면 좋을 것 같다.

Recommendation Problem

Recommendation problem은 여태까지 사용자가 item에 대해 evaluate한 history data를 기반으로 사용자가 아직 사용하지 않은 item에 대한 사용자의 평가를 예측하는 문제라고 할 수 있다. 추천과 랭킹 문제는 마케팅을 포함한 다양한 분야에서 오랜 세월 관심을 가져왔던 분야이다. 특히 광고를 제작하는 사람들 입장에서는 적은 비용으로 최대한의 효율을 낼 수 있는 타겟광고는 그야말로 금덩이나 다름없는 영역이라 할 수 있을 것이다. 추천은 그만큼 제한된 자원을 최대한 효율적으로 분배할 수 있는 방법이기도 하며, 사람들의 지갑을 더 열게 할 수 있는 중요한 문제인 것이다. Netflix와 왓챠는 내가 점수를 매긴 별점을 바탕으로 내가 좋아할만한 영화나 드라마를 추천해준다. 아마존, 이베이, Gmarket 등의 온라인 쇼핑몰들 역시 내가 클릭했던 상품들의 history를 기반으로 내가 좋아할만한, 사고싶어할만한 상품들을 추천해주거나, 이 상품들을 묶어서 하나의 작은 할인 패키지를 구성하기도 한다. 페이스북은 내가 좋아요를 누른 포스트들을 바탕으로 내가 좋아할만한 페이지를 추천하고, 타겟 광고를 내보낸다. 우리가 지금은 너무나 자연스럽게 받아들이는 이 사실들은 전부 머신러닝에 의해 가능해진 것들이다.

Matrix Completion

그러면 이제 추천 문제를 보다 엄밀하게 정의해보도록 하자. 먼저 데이터에 대해 살펴보도록 하자. 이 문제에서는 사용자와 상품이라는 두 가지 요소들이 존재한다. 사용자 $u$가 아이템 $i$를 얼마나 좋아할 것인지 나타내는 값을 rating $r_{ui}$라 하자. 이때, 이 rating은 Netflix처럼 1에서 5 사이의 real value일수도 있으며, 아마존이나 페이스북처럼 클릭했는지 하지 않았는지에 대한 데이터일수도 있다. 앞선 경우는 사용자가 자신이 얼마나 이 아이템을 좋아하는지 ‘명시적으로’ 나타냈기 때문에 explicit feedback이라 부르며, 후자의 경우는 사용자가 해당 상품을 좋아했는지 싫어했는지 표현을 직접적으로 하지 않으므로 ‘implicit feedback’이라고 부른다. 이에 대해서는 나중에 다른 글을 통해 더 자세히 다루도록 하겠다. (Implicit feedback에 대한 글을 새로 추가하였다) 지금은 $r_{ui}$의 정확한 값을 알고 있고, 이 값이 전혀 noise가 없는 값이라고 가정하고 문제를 계속 설명하도록 하겠다. 이런 경우 우리가 가지고 있는 데이터는 $r_{ui}$들의 값이 될 것이고, 대략 아래와 같은 방식으로 matrix로 표현할 수 있을 것이다.

이때 *은 아직 사용자가 평가하지 않은 데이터를 의미한다. 이제 recommendation problem은 이 매트릭스의 비어있는 부분의 값을 예측하는 문제로 바꿔서 생각할 수 있다. 이를 수식으로 표현하면 아래와 같은 형태로 표현하는 것이 가능하다.

$$\min_{\hat R} \| \hat R - R \|_F^2 $$

이때 $R$는 비어있는 곳이 없는 원래 데이터를 의미한다. User의 숫자를 n, item의 개수를 m이라고 하면 R은 n by m matrix가 될 것이다. $\hat R$는 원래 데이터로부터 비어있는 곳을 복구한 데이터를 의미한다. 여기에서, 원래 데이터 matrix $R$에서 값이 없었던 부분은 제외하고 error를 (oot mean squared error라 하여 RMSE라 부른다) 계산하는 것이 이 문제의 objective function이 된다. 이런 문제를 일컬어, 비어있는 matrix를 완성시키는 문제다 해서 Matrix Completion이라고 부른다. 따라서 앞으로 남은 글에서는 recommendation problem이라는 말 대신, matrix completion이라는 이름으로 바꿔서 부를 것이다.

Matrix Factorization

그러면 앞서 설명한 matrix completion 문제를 어떻게 해결할 수 있을까? 지금까지는 문제를 정의하는 법에 대해서만 설명했지만, 이제부터는 이 문제를 풀기 위한 가정과 그 가정을 사용하여 만든 모델, 그리고 그 모델을 풀기위한 알고리즘을 설명할 것이다. Matrix Completion 문제를 풀기 위한 방법은 여러 가지가 있다. 이전 글 [2] 에서 다뤘던 baseline predictor와 neighborhood method 등의 방법도 그런 방법들 중 하나이지만, 이 글에서는 단일 모델로 가장 우수한 성능을 보이는 것으로 알려진 matrix factorization에 대해서만 다룰 것이다. Matrix factorization의 가정은 original data matrix $R$가 low rank matrix라는 것이다. 따라서 우리가 복원하는 $\hat R$ 역시 low rank 조건을 가지게 되므로 constrained optimization 문제로 바꿔서 쓸 수 있게 된다. 이 경우 optimal한 matrix completion의 objective function은 다음처럼 표현된다.

$$\min ~\mbox{rank}(\hat R) ~\mbox{ s.t. }~ \Omega(r_{ui} - \hat r_{ui}) = 0 ~\forall u,i$$

여기에서 $\Omega(A_{ij} - B_{ij})$는 matrix A와 B의 i,j 번째 element 중 하나라도 비어있으면 0, 둘 다 element가 존재하면 둘의 차이로 정의가 된다.

이 문제를 어떻게 풀지에 대해 논하기 전에 먼저 low rank assumption은 어떤 의미가 있는지에 대해 먼저 논해보자. 먼저 모든 matrix는 다른 두 matrix의 곱으로 표현이 가능하다. 이때 만약 matrix의 rank가 작다면 두 matrix 의 rank역시 더 작은 형태로 표현이 가능하게 된다. 즉, 원래 n by m matrix R이 n이나 m보다 작은 k만큼의 rank를 가졌을 때, R은 n by k matrix P와 m by k matrix Q의 곱으로 표현할 수 있다. 즉, $R = P Q^\top$ 으로 표현이 된다는 사실이 이미 알려져있다.

$p_u$와 $q_i$는 각각 P와 Q의 u, i번째 row vector라고 정의하면 (둘 다 k차원 벡터가 된다) 앞선 수식에서부터 우리는 다음과 같은 수식을 얻을 수 있다.

$$r_{ui} = p_u \cdot q_i$$

이 사실로부터 우리는 user u가 item i의 점수를 주는 방식은, user u의 item들에 대한 숨겨진(latent) interest $p_u$와 그에 대응하는 item들의 숨겨진 특성 $q_i$에 의해 결정된다는 사실을 알 수 있다. 이를 그림으로 표현하면 다음과 같다.

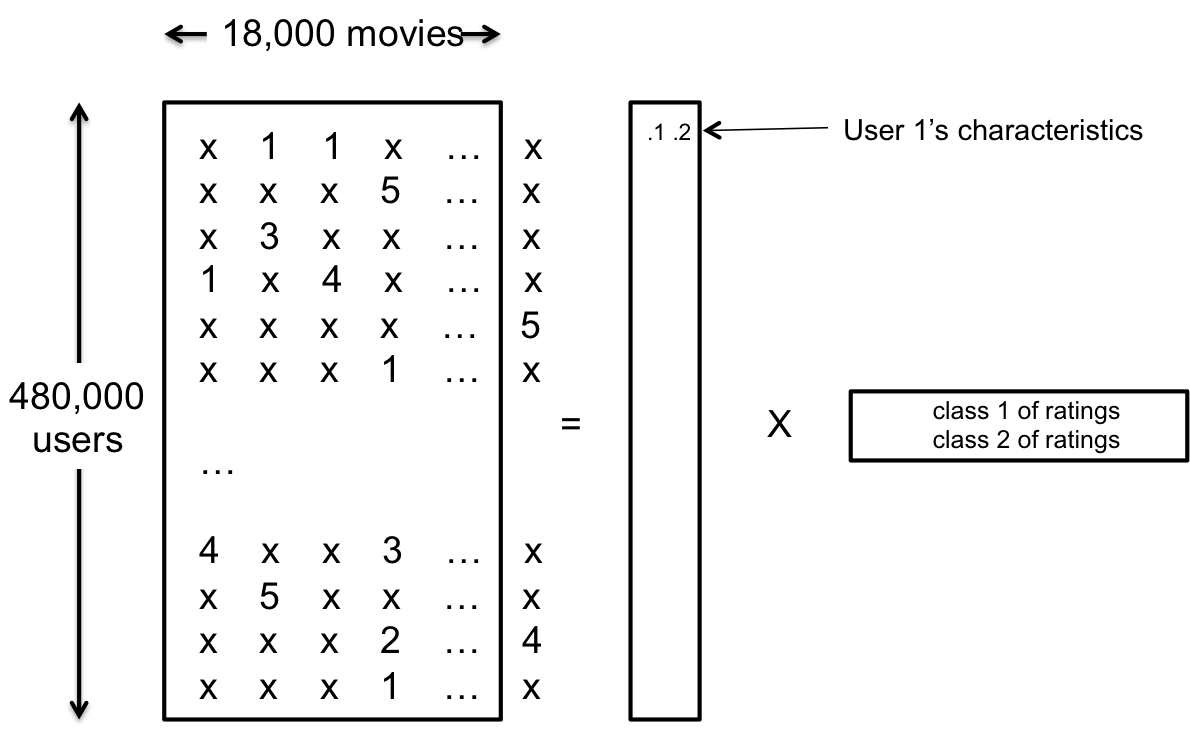
따라서 앞에서 설명했던 rank를 minimize하는 문제는, 최대한 적은 latent feature를 사용하여 user와 item을 표현하도록 하는 문제가 되는 것이다. 그러나 실제로는 rank condition이 convex optimization이 아니기 때문에 이 문제를 optimal하게 풀 수 없다는 문제점이 존재한다. 여기에서 두 가지 접근 방법이 가능하다. 하나는 rank condition을 convex 조건으로 바꿔서 푸는 convex relaxation이 있고, 또 하나는 rank의 값은 우리가 직접 넣어주는 hyper-parameter로 사용하고, 대신 RMSE를 minize하는 방법이 있다. 각각의 objective function은 다음과 같이 표현된다.

$$\min_{\hat R} \| \hat R \|_* ~\mbox{ s.t. }~ \Omega(r_{ui} - \hat r_{ui}) = 0 ~\forall u,i.$$

$$\min_{\hat R} \sum_{u,i \in \kappa} (r_{ui} - \hat r_{ui})^2 ~\mbox{ s.t. }~ \mbox{rank}(\hat R) = k.$$

여기에서 $u,i \in \kappa$는, 전체 데이터 중에서 오직 관측된 u,i pair만을 의미한다. 즉, $\Omega$ notation을 대체하는 기호라고 생각하면 된다.

전자는 항상 convex relaxed된 문제에서는 optimal한 solution을 찾을 수 있다는 것이 보장된다는 장점이 있지만, 원래 문제와 다른 문제를 풀기 때문에 원래 문제와 같은 optimal solution을 갖는 상황이 아니면 의미가 없을 수 있다는 문제점이 있다. 후자는 convex한 방법론을 사용할 수 없기 때문에 global optimal solution 대신 local optimal solution을 얻게 되지만, practical하게 잘 동작한다는 장점이 존재한다. 이 글에서는 둘 다 짤막하게 (그러나 너무 깊지 않게) 다뤄볼까 한다.

Methodology 1: Convex Relaxation

먼저 왜 rank condition이 non-convex condition인지부터 살펴보자. Matrix X의 rank는 X의 0이 아닌 singular value들의 숫자로, 다시 말해 이들의 l-0 norm의 합으로 표현이 가능하다. 즉, 원래 objective function은 다음처럼 표현할 수 있다.

$$\min \sum_\ell \| \sigma_\ell(\hat R) \|_0 ~\mbox{ s.t. }~ \Omega(r_{ui} - \hat r_{ui}) = 0 ~\forall u,i$$

이때, $\sigma_i(A)$는 A의 i번째 singular value를 의미한다. 만약 matrix의 rank k가 full rank가 아니라면, 정확하게 k개의 singular value만 값이 0이 아니고, 나머지 singular value들의 값은 0이 된다. 따라서 이 문제가 위에 적은 것 처럼 l-0 norm의 합으로 표현이 되는 것이다. 문제는 이 l-0 norm 자체가 non-convex norm이라는 것이다. 보통 l-0 norm을 relax하는 가장 tight한 방법 중 하나가, l-0 norm을 l-1 norm으로 바꾸는 것이다. 이때, matrix A의 singular value들의 l-1 norm합은, matrix A의 nuclear norm $\| A \|_* $이 된다. 따라서 위의 문제를 $ \min \sum_\ell \| \sigma_\ell(\hat R) \|_1 $으로 relax하게 될 경우 (편의상 constriant는 생략한다), objective function은 $\min \| \hat R\|_*$을 하는 것과 같다.

이 문제는 convex problem이기 때문에 아무 convex solver를 가져와서 문제를 풀면 된다. 그러나 조금 더 효율적인 풀이방법을 위하여 singular value thresholding이라는 alternating update 방식의 알고리즘도 제안이 되어있는 상태이다. 이 글에서는 최대한 개념 위주로 설명을 할 생각이기 때문에, 설명 대신 좋은 review paper [3]와 원본 논문 [4]을 reference로 추가한다.

이렇듯 convex relaxation에서 algorithm은 보통 큰 issue는 아니다. 물론 기존 solver보다 더 좋은 알고리즘을 제안하는 것도 중요한 일이지만, convex relaxation에서 가장 critical한 issue는, relaxed problem이 언제 원래 problem과 같은 해를 가지는지에 대한 조건이 무엇이냐 하는 것이다. 즉, 내가 그 어떤 조건에서도 relaxed problem을 사용해서 원래 문제를 풀 수 없다면, 그 convex relaxation은 가치가 없는 relaxation이 되는 것이다. 아마도 데이터가 많으면 많을수록 복원이 쉬울 것이고, 적으면 적을수록 복원이 어려워지다가, 어느 순간부터 복원이 불가능해지는 시점이 존재할 것이라는 것이다. 예를 들어 데이터가 하나 빼고 전부 있다면 MC가 어려운 문제가 아닐 수 있지만, 반대로 데이터가 하나만 있다면 복원할 수 있는 경우의 수가 거의 무한하게 많을 것이라는 것이다. 다행히도 리뷰 페이퍼 [3]의 Theorem 1에도 나와있듯, user와 item 숫자 중 더 큰 숫자를 $n_0$라고 했을 때, convex relaxed problem이 optimal한 solution을 얻기 위해서는 order of $n_0 \log^2 n_0$ 만큼의 observed data가 필요하다는 증명이 이미 되어있다. 이에 대한 자세한 설명은 해당 논문을 읽어보면 좋을 것 같고, 이 글에서는 생략하도록 하겠다.

Methodology 2: Solve Non-convex Problem Directly

두 번째 방법으로는 non-convex한 objective function을 바로 푸는 것이다. 혼동을 피하기 위하여 이 objective function을 다시 적어보자.

$$\min_{\hat R} \sum_{u,i \in \kappa} (r_{ui} - \hat r_{ui})^2 ~\mbox{ s.t. }~ \mbox{rank}(\hat R) = k.$$

그리고, 이미 앞에서 $\hat r_{ui} = p_u \cdot q_i$로 표현할 수 있다는 것 까지 확인했었으므로, 이를 기반으로 문제를 적으면 다음과 같은 문제가 된다.

$$\min_{P,Q} \sum_{u,i \in \kappa} (r_{ui} - p_u \cdot q_i)^2.$$

앞에서 설명한 것 처럼 P,Q는 각각 n by k, m by k matrix가 된다. 이때, overfitting을 피하고 보다 generalized된 문제로 바꿔주기 위하여 regularization term을 뒤에 붙여주면 문제는 다음과 같이 바뀐다.

$$\min_{P,Q} \sum_{u,i \in \kappa} (r_{ui} - p_u \cdot q_i)^2 + \lambda ( \| p_u \|_2^2 + \| q_i \|_2^2 ) .$$

이 pair-wise optimization 문제는 non-convex 문제이지만, gradient descent method로 local optimum에 수렴하는 결과를 얻을 수 있으며 실제로 꽤 효율적으로 좋은 결과를 얻을 수 있다.

또 다른 solver로는 Alternating Least Square (ALS) 라는 방법이 있다. 이 방법은 alternative하게 주어진 objective를 update하는 방법인데, 주어진 objective가 pairwise optimization으로 생각하면 non-convex이지만, p나 q 중 하나를 고정하고 나머지에 대해 optimization을 하게 되면 convex, 그것도 closed form으로 계산된다는 점을 이용한 방법이다. 따라서 이 방법을 사용해 예전에 설명했었던 k-means style의 알고리즘을 설계할 수 있는데, 이를 ALS라고 부르는 것이다. Gradient descent가 더 빠른 경우도 있지만, ALS를 사용하게 되면 각각의 element들이 다른 element에 independent하기 때문에 분산처리가 간편하기 때문에 실제로는 ALS 방법도 많이 사용된다고 한다.

지금까지 설명한 방법은 그야말로 가장 기본이 되는 모델이고, 이 모델을 조금 더 확장해보도록 하자. 가장 간단하게 확장할 수 있는 방법은 bias term을 추가하는 것이다. 예를 들어서 어떤 user는 항상 모든 영화 평점을 비교적 ‘짜게’ 주는 user가 있을 수 있고, 반대로 모든 영화에 점수를 후하게 주는 user도 있을 수 있다. 어떤 영화는 개봉 전부터 평단이나 기자들에게서 호평을 받았거나 유명 배우가 나와 기본 점수가 높을 수도 있고, 그 반대도 가능하다. 따라서 이런 현상들을 반영할 수 있는 bias term이 추가가 되는 것은 지극히 자연스럽다고 할 수 있다. user의 bias를 $b_u$, item의 bias를 $b_i$라고 하면 (이 값들은 vector가 아니라 scalar value이다) user u의 item i에 대한 bias $b_{ui}$는 $b_{ui} = \mu + b_u + b_i$로 표현할 수 있을 것이다. 여기에서 $\mu$는 전체 모든 r_{ui}의 평균 값으로, bias라는 개념이 평균에서부터 얼마나 멀어지는 가에 대한 개념이므로 평균 값도 함께 고려하는 것이다. $\mu$는 데이터와 함께 주어지는 값이고, bias term들은 p,q처럼 optimization을 통해 찾아야하는 optimization parameter가 된다. 이를 사용하면 reconstructed rating $\hat r_{ui}$는 다음과 같이 표현된다.

$$\hat r_{ui} = \mu + b_u + b_i + p_u \cdot q_i.$$

이제 이 결과를 원래 objective에 대입하면 다음과 같은 식을 얻게 된다.

$$\min_{P,Q,B} \sum_{u,i \in \kappa} (r_{ui} - \mu - b_u - b_i - p_u \cdot q_i)^2 + \lambda ( \| p_u \|_2^2 + \| q_i \|_2^2 + b_u^2 + b_i^2 ) .$$

마찬가지로 이 결과 역시 gradient method나 ALS로 푸는 것이 가능하다.

Matrix Factorization in Netflix Prize Competition

위의 methodology 2는 실제로 Netflix problem에서 ([1] 참고) 단일 성능이 가장 우수했던 알고리즘을 소개한 것이다. 조금 더 구체적으로는 다음과 같은 그래프로 표현할 수 있다. (출처: [5])

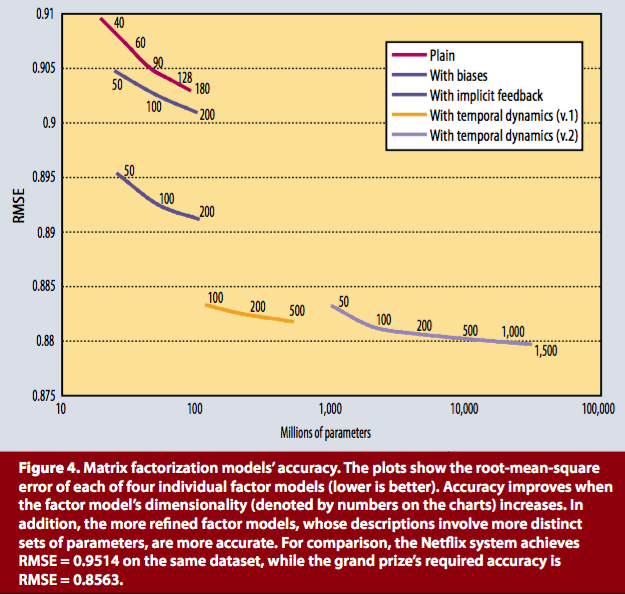
Plain은 진짜 가장 기본 term만 사용한 것이고, with bias는, 앞에서 설명한 bias를 사용한 방식이다. Implicit feedback은 생략하고, temporal dynamics는 rating이 시간에 따라 바뀐다고 가정하고 다음과 같이 모델을 설계한 것이다.

$$\hat r_{ui}(t) = \mu + b_u(t) + b_i(t) + p_u(t) \cdot q_i.$$

여기에서, item의 성질 $q_i$는 static하다고 가정하고, 대신 사람이 평가하는 방식인 $p_u$만 시간에 대해 변한다고 가정하는 것이다. 이 모델은 시간이 지남에 따라 사람들이 서로 상호작용하고, 그로 인해 별점을 매기는 방식이 바뀔 수 있다는 것을 가정으로 한 방법으로, 실제 최종 결과를 살펴보면 이 방식을 채용한 방법이 가장 우수한 결과를 얻는 것을 확인할 수 있다. 실제 Netflix prize에서는 다른 방법들까지 고려한 ensemble method가 더 좋은 성능을 내지만, 실제로 RMSE metric에서 단일 모델로 가장 좋은 성능을 내는 것은 여전히 matrix factorization 기반 접근법이다.

정리

이 글에서는 recommendation 문제가 어떤 문제인지 설명하고, 보다 수학적으로 정의된 matrix completion 문제로 recommendation을 설명한다. 그 후 이 문제를 푸는 가장 popular한 방법인 matrix factorization에 대해서 다룬다. 해당 문제가 non-convex 문제이기 때문에 convex relaxation을 통해 문제를 푸는 방법 (더 늦게 나온 방법이다), non-convex optimization을 바로 푸는 방법 (Netflix prize에서 실제 사용했던 방법) 두 가지를 소개하고 각각에 대해 간략하게 설명한다. 실제 recommendation은 matrix factorization 뿐 아니라 여러 다른 methodology들을 결합해서 문제를 풀게 되지만, 여전히 단일 model로 가장 좋은 performance를 보여주는 것은 matrix factorization을 기반으로 한 방법론들이기 때문에 matrix factorization을 제대로 아는 것이 recommendation 문제를 풀기 위한 첫 걸음이라 할 수 있을 것이다.

변경 이력

• 2016년 3월 1일: 글 등록

References

1. 인터넷 속의 수학 - How Does Netflix Recommend Movies? (1/2)
2. 인터넷 속의 수학 - How Does Netflix Recommend Movies? (2/2)
3. Kennedy, Ryan. “Low-rank matrix completion.”, 2013
4. Candès, Emmanuel J., and Benjamin Recht. “Exact matrix completion via convex optimization.”, 2009
5. Koren, Yehuda, Robert Bell, and Chris Volinsky. “Matrix factorization techniques for recommender systems.”, 2009

---

Machine Learning 스터디의 다른 글들

• Machine Learning이란?
• Probability Theory
• Overfitting
• Algorithm
• Decision Theory
• Information Theory
• Convex Optimzation
• Classification Introduction (Decision Tree, Naïve Bayes, KNN)
• Regression and Logistic Regression
• PAC Learning & Statistical Learning Theory
• Support Vector Machine
• Ensemble Learning (Random Forest, Ada Boost)
• Graphical Model
• Clustering (K-means, Gaussian Mixture Model)
• EM algorithm
• Hidden Markov Model
• Dimensionality Reduction (LDA, PCA)
• Recommendation System (Matrix Completion)
  • Recommendation System with Implicit Feedback
• Neural Network Introduction
• Deep Learning 1 - RBM, DNN, CNN
• Reinforcement Learning
  • Multi-armed Bandit